Содержание.

Введение. ………………………………………………………………………. 1

1. Тарифная политика с учетом вероятности неразорения страховой копании. ….......…………………………………………………. 4

1. 1. Точный расчет вероятности разорения. …………………………… 4

1. 2. Приближенные методы расчета вероятности разорения. …...….. 11

1. 3. Принципы назначения страховых премий. ………………………. 18

2. Сравнение рисковых ситуаций. Теория полезности. ………... 18

2. 1. Функция полезности. ……………………………………………… 24

2. 2. Типовые функции полезности дохода. Представление Неймана - Моргенштерна. .…………………………………………….………………….. 26

3. Тарифная политика с учетом функции полезности. ………… 32

Приложение 1. ……………………………………………………………… 40

Приложение 2. …………………………………………………….... 42

Приложение 3 (программа). …………………………………………… 43

Список использованной литературы. …………………………………….. 47

Введение.

Договора страхования заключаются для того, чтобы избавиться от финансовых потерь, связанных с неопределенностью наступления тех или иных случайных событий. До заключения договора страхования клиент имел некоторый риск, который мог привести к случайным потерям Х (а мог и не привести к ним). После заключения договора страхования, заплатив некоторую сумму d, клиент избавился от этого риска. Иными словами, клиент идет на небольшие детерминированные расходы с тем, чтобы избавиться от случайных потерь, которые хоть и маловероятны, но могут быть катастрофически большими для него. Однако, сам риск не исчез – его приняла на себя страховая компания. Поэтому финансовый риск и связанная с ним опасность разорения объективно присутствуют в деятельности любой страховой компании. Оценка этого риска представляет фундаментальный интерес для компании и служит основой для принятия важнейших решений.

Проблема обеспечения финансовой устойчивости страховой компании является комплексной, ее изучение и решение предполагает усилия специалистов в разных областях, прежде всего руководства компании, юристов, экономистов. Однако многие важные задачи носят чисто математический характер. В рамках теории риска разработана система понятий, моделей и методов, которые позволяют количественно оценивать финансовые риски в деятельности страховой компании. Общематематической базой для теории риска служат теория вероятности и математическая статистика.

Цель данной дипломной работы: выяснить, какой должна быть стоимость договора страхования, а главное, каким образом решается данный вопрос, используя методы теории полезности.

Структура работы определяется ее целью. Диплом состоит из трех глав и приложений.

В первой главе «Тарифная политика с учетом вероятности неразорения страховой копании» исследован традиционный подход к назначению страховой премии, когда известны только средние значения и дисперсии индивидуальных исков и определен уровень безопасности  - вероятность неразорения.

В первой главе «Сравнение рисковых ситуаций. Теория полезности» исследована теория ожидаемой полезности Неймана – Моргенштерна, рассмотрены различные классы функции полезности, определяемые коэффициентом абсолютного неприятия риска.

Наконец, в третьей главе «Тарифная политика с учетом функции полезности» исследован вопрос о влиянии предпочтений клиента или страховой компании при определении стоимости страховки, получены результаты для различных типов функции полезности.

В приложении 3 описана программа, разработанная для решение практических задач.

1. Тарифная политика с учетом вероятности неразорения страховой копании.

1. 1. Точный расчет вероятности разорения.

Модель индивидуального риска – это простейшая модель функционирования страховой компании, предназначенная для расчета вероятности разорения. Она базируется на следующих предположениях:

1. Анализируется фиксированный относительно короткий (так что можно пренебречь инфляцией и не учитывать доход от инвестирования) промежуток времени – обычно это один год;

2. Число договоров страхования N и неслучайно;

3. Плата за страховку вноситься полностью в начале анализируемого периода, никаких поступлений в течение этого периода нет;

4. Известны статистические свойства связанного с отдельным договором страхования индивидуального иска X (поскольку не все договора приводят к иску, некоторые из случайных величин Х₁, …, Х_N, где Х_i - выплата i-му клиенту, равны нулю).

В рамках этой модели разорение определяется суммарным иском

S_N = Х₁ + … + Х_N

к страховой компании. Если этот суммарный иск больше, чем резервы компании, то компания не сможет выполнить все свои обязательства и разориться. Поэтому вероятность разорения компании равна

R = P(Х₁ + … + Х_N > W) (1. 1. 1.)

Иными словами, вероятность разорения – это дополнительная функция распределения величины суммарного иска к компании за рассматриваемый промежуток времени.

Предположим, что в модели (1. 1. 1.) случайные величины Х₁, …, Х_N – независимы (таким образом, исключаем катастрофические несчастные случаи, влекущие иски сразу по нескольким договорам).

Поскольку суммарный иск представляет собой сумму независимых случайных величин, его распределение может быть посчитано с помощью классических теорем и методов теории вероятностей.

Прежде всего это использование сверток. Пусть η₁ и η₂ – две независимые, неотрицательные случайные величины с функциями распределения F₁(x) и F₂(x) соответственно, то функция распределения их суммы η₁ + η₂ может быть посчитана по формуле:

F(x) = (1. 1. 2.)

Применяя формулу (1. 1. 2.) несколько раз, мы можем посчитать функцию распределения суммы любого числа слагаемых.

Если η₁ и η₂ – непрерывны, то обычно работают с плотностями f₁(x), f₂(x). Плотность суммы может быть посчитана по формуле

f(x) = (1. 1. 3.)

Если η₁ и η₂ – целочисленны, то вместо функции распределения обычно работают с распределениями

р₁(n) = P( η₁ = n), р₂(n) = P( η₂ = n).

Распределение суммы р(n) = P( η₁ + η₂ = n) может быть определено по формуле:

р(n) = (1. 1. 4.)

После подсчета свертки последовательностей р₁(n) и р₂(n) удобно образовать матрицу вида:

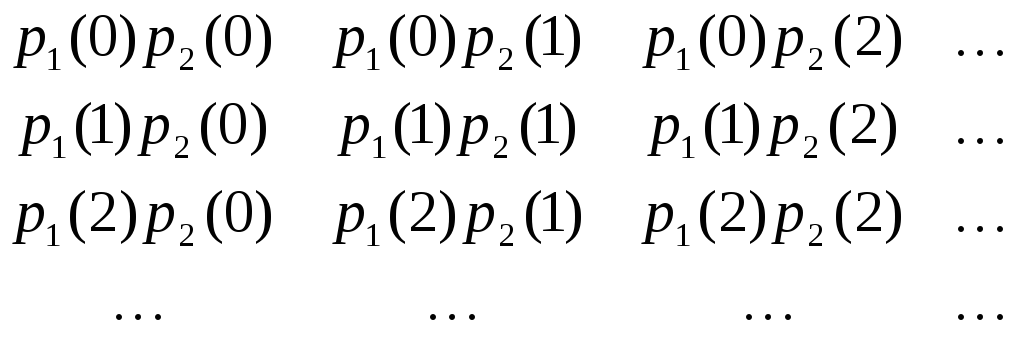
Таким образом, элемент (i, j) этой матрицы равен произведению р₁(i)р₂(j). Суммируя по линиям i + j = k, параллельным главной диагонали, получим

р₁(k)р₂(0) + р₁(k - 1)р₂(1) + … + р₁(0)р₂(k),

т. е. в точности р(k).

Подсчет вероятности разорения часто упрощается, если использовать производящие функции (для дискретных величин) или преобразования Лапласа (для произвольных неотрицательных величин).

Если слагаемые Х_i имеют дискретное распределение, независимы и одинаково распределены, то они имеют одну и ту же производящую функцию g(z) = . Соответственно, их сумма имеет производящую функцию:

g_SN(z) = g₁(z)… g_N(z) = (g₁(z))^N = (1. 1. 5.)

Отбирая коэффициенты при степенях z, получаем таблицу для вероятностей p(n).

Модель коллективного риска базируется на следующих упрощающих предположениях:

1. Анализируется фиксированный относительно короткий (так что можно пренебречь инфляцией и не учитывать доход от инвестирования) промежуток времени;

2. Плата за страховку вноситься полностью в начале анализируемого периода, никаких поступлений в течение этого периода нет;

3. Поступающие иски Y₁, Y₂, … не связываются с конкретными договорами, а рассматриваются как результат суммарного риска компании. Иными словами, Y_i - это не иск от i – го договора, а i – ый по порядку реально поступивший иск; случайные величины Y_i – независимы, одинаково распределены, строго положительны.

4. В качестве суммарной характеристики портфеля рассматривается не число заключенных договоров N, а общее число исков  за рассматриваемый период. Случайные величины  и Y₁, Y₂, … - независимы.

Так же, как и в модели индивидуального риска, в модели коллективного риска разорение определяется суммарным иском

S_ = Y₁ + … + Y_

к страховой компании. Вероятность разорения компании определяется также и равна

R = P(Y₁ + … + Y_ > W). (1. 1. 6.)

Обозначим _ = P( = n) – распределение числа исков. Поскольку случайные величины , Y₁, Y₂, … - независимы, а

Р(Y₁ + … + Y_ > W |  = 0) = P(0 > W) = 0,

мы получим

R =

Вероятности P(Y₁ + … + Y_n > W) могут быть определены с помощью сверток (1. 1. 2.). Если Y_i - непрерывны, то

P(Y₁ + … + Y_n > W) = ,

где f_{Y1 + … + Yn}(x) – плотность суммы Y₁ + … + Y_n. В этом случае предпочтительнее использовать формулу (1. 1. 3.) и записывать вероятность разорения в виде

R = ,

где

плотность суммарного иска.

Если Y_i - дискретные, то

P(Y₁ + … + Y_n > W) = ,

где

распределение суммы Y₁ + … + Y_n. В этом случае использовать формулу (1. 1. 4.) и записывать вероятность разорения в виде

R = ,

где

распределение суммарного иска.

Как уже отмечалось, вычисления с суммами упрощается, если использовать производящие функции (для дискретных величин) или преобразования Лапласа (для произвольных неотрицательных величин).

Обозначим через

производящую функцию числа исков, а через

преобразование Лапласа величины предъявленного иска (поскольку все предъявляемые иски одинаково распределены, (s) не зависит от номера i).

Тогда для преобразования Лапласа Ф(s) = E[e^sS] суммарного иска имеем:

Ф(s) = =

= = ((s)). (1. 1. 7.)

Из формулы (1. 1. 7) дифференцированием по s в точкеs=0 можно получить следующие формулы

E[S_] = E[Y] E[] (1. 1. 8.)

D[S_] = D[](E[Y])² + D[Y]E[] (1. 1. 9.)

Если иски дискретны, известна производящая функция g(z) = E[z^Yi], то

G(z) = ( g(z)). (1. 1. 10.)

Предположим, что число исков  имеет распределение Пуассона со средним:

_i=P( = i) =,i = 0, 1, 2, …

В этой ситуации распределение величины суммарного иска S_ называется составным пуассоновским распределением.

Параметр  исходного пуассоновского распределения_iи распределениеF(x) искаY называютпараметрами составного пуассоновского распределения.

Преобразования Лапласа величины S_ может быть получено из (1.1. 7.) при (z) = e^{(z - 1)}:

Ф(s) = e^{((s) - 1)}, (1. 1. 11.)

где (s) - преобразование Лапласа величины предъявленного иска.

Если Y_i - дискретные с производящей функцией g(z), то составное пуассоновское распределение также является дискретным и его производящая функция дается формулой:

G(z) =e^{(g(z) - 1)}. (1. 1. 12.)

Учитывая, что E[] =D[] =и формулы (1.1. 8), (1. 1. 9), имеем

E[S_] = E[Y] (1. 1. 13.)

D[S_] = E[Y²] (1. 1. 14.)

Составное пуассоновское распределение обладает рядом специальных свойств, которые представлены в приложении 1.

Самым эффективным методом точного расчета распределения P_n=P(S_=n) составного пуассоновского распределения с дискретным распределениемp_n величины предъявляемых исков является использовании следующей рекуррентной формулы:

Предположим, что число исков  имеет отрицательное биномиальное распределение с параметрамиpи, т. е.

_i=P( = i) =,i = 0, 1, 2, …,

где q= 1-p.

В этой ситуации распределение величины суммарного иска S_ называется составным отрицательным биномиальным распределением.

Преобразования Лапласа величины S_ может быть получено из (1.1. 7.) при (z) = :

Ф(s) = , (1. 1. 15.)

где (s) - преобразование Лапласа величины предъявленного иска.

Параметры pи исходного отрицательного биномиального распределения_iи распределениеF(x) искаY называютпараметрами составного отрицательного биномиального распределения.

Если Y_i - дискретные с производящей функцией g(z), то составное отрицательное биномиальное распределение также является дискретным и его производящая функция дается формулой:

G(z) =.

Для моментов составного отрицательного биномиального распределения из общих формул (1. 1. 8), (1. 1. 9), имеем

E[S_] =E[Y] (1. 1. 16.)

D[S_] =E[Y²] (1. 1. 17.)

Каждое составное отрицательное биномиальное распределение можно рассматривать как составное пуассоновское распределение с определенным образом подобранными параметрами. Этот вопрос подробно рассмотрен в приложении 2.

Справедлива следующая рекуррентная формула для расчета распределения суммарного иска:

,

где p_i – распределение величины предъявляемых исков.