2.2. Характеристический коэффициент.

Основополагающую роль в анализе вероятности разорения 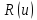играет так называемый характеристический коэффициент (или коэффициент Лундберга). Определяется как положительное решение характеристического уравнения относительно:

где а относительная защитная надбавка определяется формулой (2.1.4), поэтому (2.2.1) можно переписать в виде:

Рассмотрим вопрос о существовании и способах вычисления характеристического коэффициента. Отметим, что 𝔼это преобразование Лапласа величины иска в точке

Поэтому функция определена для

Мы будем рассматривать только такие распределения величины иска, для которых функция определена при некотором(условие Крамера). Поскольку

то

По этой причине часто называют производящей функцией моментов (хотяявляется производящей функцией нормированных моментов и только в случае, если эти моменты действительно существуют).

Поскольку при верно неравенството из конечностиследует конечность. Поэтому область определения функции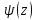всегда является связным промежутком видаили, где абсцисса сходимости(которая положительна в силу условия Крамера) может быть равна.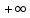

Пусть, например, экспоненциальная плотность с параметромβ. Тогда преобразование Лапласа определено дляи дается формулойСоответственно, производящая функция моментовопределена дляи равна

Пусть теперь величина иска ограничена. Тогдапри всех

Если область определения производящей функции моментов – открытый промежуток 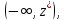то(в противном случае, в силу теоремы Леви,). При этом, если, то поскольку, функциявозрастает быстрее, чем любая линейная функция.

Если область определения производящей функции моментов – замкнутый справа промежуток , то в силу теоремы Лебега

Поскольку то функциявсегда монотонно возрастает и выпукла вниз. Кроме тогоПоэтому график функциивыходит из точкипод углом, меньшим, чем прямая

Если область определения функции – открытый промежутокто из описанного выше характера поведения функцииясно, что графики функцийиприобязательно пересекутся и при том только в одной точке: это и будет характеристический коэффициент.

Если область определения функции 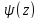– замкнутый справа промежутокто ясно, что характеристический коэффициент существует тогда и только тогда, когда

В качестве примера определим характеристический коэффициент, если распределение величин исков является экспоненциальным с параметром

Для экспоненциального распределения производящая функция моментов есть

Поэтому характеристическое уравнение (2.2.1) выглядит следующим образом:

т.е.

Оно имеет тривиальный корень и единственный положительный корень

который по определению и является характеристическим коэффициентом.

2.3. Неравенство Лундберга.

Вероятность разорения можно получить как предел привероятностейтого, что компания разорится не позже, чем после предъявленияпервых исков. Дополнительная вероятностьявляется вероятностью того, что первыеисков не приведут к разорению. В силу (2.1.2)

По формуле полной вероятности

где

При условии, что событие– достоверно. Поэтому в пересечении в правой части формулы (2.3.3) его можно не учитывать. Кроме того, присобытиеможно переписать в видегдеПоскольку случайные величины– независимы в совокупности, получаем:

Далее, случайные величины одинаково распределены. Поэтому последовательностьсовпадает по распределению с последовательностью. По той же причине последовательность. Следовательно,

Сопоставляя эту вероятность с правой частью формулы (2.3.1), видно, что она равна Теперь уравнение (2.3.2) примет вид:

Это уравнение можно записать и в форме

(2.3.5)

Проведенное доказательство уравнения (2.3.4) базируется на очень простой идее: если в момент предъявления первого иска компания не разорится т.е. если, то она по существу начинает функционировать заново, но с измененной величиной начального резерва, равной

Используя формулу (2.3.5), докажем по индукции, что

где – характеристический коэффициент.

Действительно, и поэтому длянеравенство (2.3.6) верно тривиально.

Предположим теперь, что неравенство (2.3.6) истинно для значения Тогда с помощью уравнения (2.3.5) имеем:

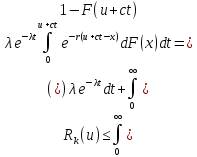
Поскольку в интеграле переменная, верно неравенство:

Теперь мы можем продолжить оценивание

На заключительном шаге наших преобразований используется тот факт, что удовлетворяет уравнению (2.2.1).

Переходя к пределу при в неравенстве (2.3.6), получимоценку Лундберга для вероятности разорения:

Более тонкий математический анализ показывает, что при

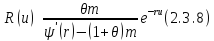
Этот результат известен как теорема Крамера-Лунберга.

Имея в виду неравенство (2.3.7) и асимптотику Крамера-Лундберга (2.3.8), можно сказать, что вероятность разорения мала, если характеристический коэффициент большой. Иными словами, характеристический коэффициент, который включает в себя основные параметры модели (интенсивность поступления исков, распределение величин исковскорость поступления премий), является интегральной характеристикой финансовой безопасности компании.