
Учебное пособие. Механика грунтов
.pdf110
фундамента определяют максимальную осадку по оси z. В случае
внецентренно нагруженного фундамента определяют величину средней осадки и крена (тангенса угла наклона подошвы фундамента).
Различают две группы методов расчета осадок: основанные на строгих решениях и приближенные решения.
Из строгих решений можно выделить метод определения осадок линейно- деформируемого полупространства или слоя ограниченной мощности (метод общих упругих деформаций). Осадку центрально загруженного фундамента s
можно определить по формуле
s = |
ω× p ×b ×(1 - v2 ) |
, |
|
0 |
|||
|
|
||
|
E |
|
где: ω – табличный коэффициент, принимаемый по приложению И, в зависимости от формы площади, жесткости фундамента, а также от мощности слоя; p0 – дополнительное давление под подошвой фундамента, равное p – γ·d; E и v – модуль деформации и коэффициент Пуассона грунта основания.
Недостатком данного метода является невозможность применения в условиях неоднородного напластования грунтов основания, а также
невозможность учета напряженного состояния грунтов основания с глубиной, что дает завышенные значения осадок.
Приближенные методы расчета обладают большой универсальностью и основаны на ряде упрощений. Первое упрощение учитывает, что природное давление увеличивается, а дополнительные напряжения уменьшаются с глубиной, следовательно, основные осадки будут происходить в верхней части основания. Поэтому вводят понятие глубины сжимаемой толщи основания Нс – такой мощности слоя, деформации которого будут определять величину осадки. Остальные упрощения сводятся к выделению в пределах сжимаемой толщи нескольких элементарных слоев грунта (слоев такой толщины, для которых можно, без особых погрешностей, принимать в
111
расчетах средние значения действующих напряжений и средние значения характеризующих грунты коэффициентов), определению сжатия элементарных слоев под действием дополнительной нагрузки, распределенной по поверхности элементарного слоя, и получения значения осадки посредством суммирования величин сжатия элементарных слоев.
Сжатие элементарных слоев грунта рассматривается без возможности бокового расширения и с возможностью бокового расширения грунта.
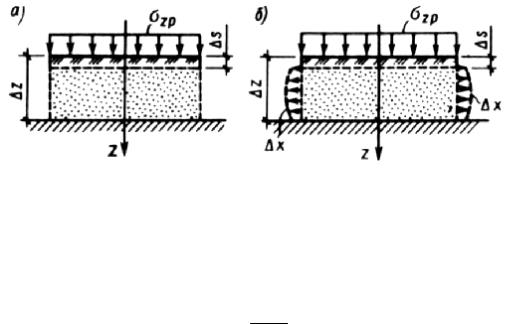
В случае действия сплошной нагрузки интенсивностью р, распространенной на значительные расстояния в стороны, элементарный
слой грунта будет испытывать только сжатие без возможности бокового расширения (рис. 68 а). Сжатие без возможности бокового расширения будет
аналогично компрессионному сжатию грунта в невысоком цилиндре с жесткими стенками (сжатие в одометре). Следовательно, осадка грунта произойдет вследствие уменьшения объема пор в грунте n, а объем твердых частиц m будет неизменен.
Рис. 68. Расчетные схемы элементарного слоя грунта без возможности бокового расширения (а) и с возможностью бокового расширения (б)
Выделим в рассматриваемом элементарном слое грунта на всю его высоту h цилиндр площадью поперечного сечения F. Учитывая, что
m = 1+1 e ,
приравняем в рассматриваемом цилиндре объем твердых частиц до приложения нагрузки к объему твердых частиц после полного компрессионного уплотнения под нагрузкой

112
1 |
× F × h = |
1 |
× F ×h' , |
|
|
||
1 + e1 |
1 + e2 |
||
где: е1 – коэффициент пористости грунта, соответствующий условиям естественного залегания (определяемый по значениям γ, ω и γs); е2 – коэффициент пористости грунта, соответствующий значению внешней нагрузки интенсивностью р (определяемый по компрессионной кривой).
Сокращая обе части полученного уравнения на F и решая относительно h'
получим
h' = h × 1 + e2 . 1 + e1
Величина сжатия элементарного слоя s будет равна разности высот
рассматриваемого цилиндра грунта до уплотнения под нагрузкой и после уплотнения, следовательно
æ |
|
|
1+ e2 |
ö |
|
e1 - e2 |
|
|
ç |
1 |
- |
÷ |
= h × |
. |
|||
1+ e |
1+ e |
|||||||
s = h - h' = h ×ç |
÷ |
|||||||
è |
|
|
1 |
ø |
|
1 |
|
В соответствии с законом компрессионного уплотнения грунтов e1 - e2 = m0 (p2 - p1 )= m0 × p ,
следовательно, можно записать
s = h × 1m+0e1 × p .
Поскольку коэффициент относительной сжимаемости mv определяется по
формуле
mv = 1m+0e1 ,
получим наиболее простой вид формулы, заменив р на σzp s = σzp ×Eh × β = σzp × h × mv ,
113
где: σzp – дополнительные напряжения в середине элементарного слоя; h – толщина элементарного слоя; β – коэффициент, учитывающий возможность бокового расширения грунта; E – модуль деформации грунта; mv – коэффициент относительной сжимаемости, равный β/Е.
Величину сжатия элементарного слоя грунта s с возможностью бокового расширения (рис. 68 б), в условиях пространственной задачи,
можно определить по формуле
æ σ |
z |
- σ |
m |
|
σ |
ö |
|
||
s = h ×ç |
|
|
+ |
|
m |
÷ |
, |
||
|
2 ×G |
|
|
|
|||||
è |
|
|
|
K ø |
|
||||
где: h – толщина элементарного слоя; G – модуль сдвига; К – модуль объемной деформации; σz и σm – компоненты напряжений в середине слоя.
Методы расчета, учитывающие возможность бокового расширения, позволяют получать более точные результаты, однако они более трудоемки и требуют сложных экспериментов (для определения G и К требуются испытания грунта по схеме трехосного сжатия). Поэтому методы расчета, учитывающие возможность бокового расширения, применяют при проектировании сложных и ответственных сооружений. Методы расчета, не учитывающие возможность бокового расширения, более просты, не требуют проведения сложных экспериментов (значения Е или mv определяют в ходе компрессионных испытаний), и приемлемы для большинства сооружений промышленного и гражданского строительства.
9.3. Практические методы расчета стабилизированных осадок
Расчет осадок методом послойного суммирования без учета возможности бокового расширения грунта рекомендован СНиП 2.02.01-83* "Основания зданий и сооружений" и является основным при расчетах осадок фундаментов промышленного и гражданского строительства.
114
Первоначально проводят совмещение оси фундамента с геологической колонкой грунтов (рис. 69).
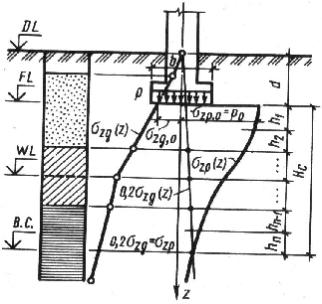
Рис. 69. Геологическая колонка и расчетная схема для определения осадок методом послойного суммирования:
DL – планировочная отметка земли; FL – отметка подошвы фундамента; WL – отметка уровня подземных вод; В.С. – нижняя граница сжимаемой толщи
Зная нагрузки от сооружения, определяют среднее давление на грунт по подошве фундамента р (определение контактных напряжений рассмотрено в п. 5.2). Затем, начиная от планировочной отметки земли, строят эпюру природного давления по оси фундамента. Зная природное давление на уровне подошвы фундамента σzg,0 определяют дополнительное вертикальное напряжение в плоскости подошвы фундамента р0 = σzр,0 = р – σzg,0. Далее
определяют дополнительные напряжения по оси фундамента и строят их эпюру (определение напряжений в грунтовом массиве рассмотрено в п. 5.3). Построив эпюры природного давления и дополнительных напряжений, определяют нижнюю границу сжимаемой толщи по условию σzр(z) = 0,2·σzg(z) (в случае залегания в пределах этой глубины слабых грунтов с Е < 5 МПа условие будет иметь вид σzр(z) = 0,1·σzg(z)). Данную операцию удобно проводить графически, для чего эпюру природного давления, уменьшенную в 5 или 10 раз совмещают с эпюрой дополнительных напряжений. Точка
115
пересечения данных эпюр определяет положение нижней границы сжимаемой толщи. Для грунтов, обладающих структурной прочностью,
некоторые исследователи рекомендуют определять нижнюю границу сжимаемой толщи по условию σzр(z) = σstr.
Сжимаемую толщу основания разбивают на n элементарных слоев при условии, что грунт в пределах элементарного слоя должен быть однородным. Толщину элементарного слоя принимают не более 0,4·b, а для фундаментов с b > 4 м – не более 0,2·b.
Осадку фундамента находят как сумму величин сжатия каждого элементарного слоя в пределах сжимаемой толщи по формуле
n |
n |
β × h ×σ |
zр,i |
|
s = åhi × mv ,i ×σzр,i =å |
i |
|||
|
|
, |
||
E |
|
|||
i=1 |
i=1 |
0,i |
|
|
где: n – количество слоев в пределах сжимаемой толщи; hi – толщина i-го слоя грунта: mv.i – коэффициент относительной сжимаемости i-го слоя грунта; σzр,i – дополнительное напряжение в середине i-го слоя грунта; Е0,i – модуль деформации i-го слоя грунта; β – коэффициент, зависящий от бокового расширения грунта (допускается принимать равным 0,8).
Для случая расчета осадок методом послойного суммирования с учетом возможности бокового расширения грунта все предыдущие построения сохраняют, а осадку фундамента находят по формуле
n |
æ |
σ |
zp ,i |
- σ |
mp,i |
|
σ |
|
ö |
|
|
ç |
|
|
|
|
mp,i ÷ |
||||
s = åç |
|
|
|
|
+ |
|
|
|
÷ , |
|
|
2 ×Gi |
|
|
|
|
|||||
i=1 |
è |
|
|
|
Ki ø |
|||||
где: σzр,i и σmp,i – компоненты |
напряжений |
в |
середине i-го слоя грунта; |
|||||||
Gi и Кi – модуль сдвига и модуль объемной деформации i-го слоя грунта.
Учет влияния соседних загруженных площадей и фундаментов проводят в случае, если они расположены в непосредственной близости от
рассчитываемого фундамента и дополнительное давление от них приведет к увеличению осадки рассчитываемого фундамента. Для решения этой задачи используют метод угловых точек. Определенное по методу угловых точек
116
дополнительное давление от соседних загруженных площадей и
фундаментов плюсуют к значениям дополнительного давления |
от |
рассчитываемого фундамента (рис. 70). |
|
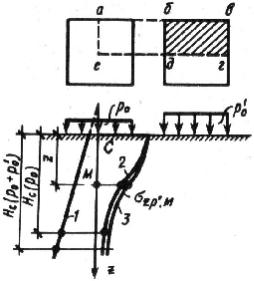
Рис. 70. Расчетная схема для учета влияния соседних фундаментов:
1 – эпюра природного давления; 2 – эпюра дополнительных напряжений по оси фундамента от нагрузки р0; 3 – эпюра дополнительных напряжений по оси фундамента от нагрузки р0 + р'0
Расчет осадок методом эквивалентного слоя, предложенным Цытовичем,
дает возможность упрощения техники расчета конечных осадок и их развития во времени. Эквивалентным слоем называют такой слой грунта hэ,
осадка которого при сплошной нагрузке на поверхности будет равна осадке грунтового полупространства под воздействием местной нагрузки той же интенсивности.
В условиях однородного основания мощность эквивалентного слоя грунта равна
hэ = Aω ×b ,
где: Аω – коэффициент эквивалентного слоя (определяется по приложению М в зависимости от вида грунта, коэффициента Пуассона v и соотношения сторон фундамента); b – ширина подошвы фундамента.
117
Криволинейную эпюру дополнительных напряжений по оси фундамента заменяют на эквивалентную треугольную с вершиной на глубине hэ (рис. 71 а). Зная размер эквивалентного слоя грунта, осадку фундамента заданного
размера и формы определяют по формуле
s = hэ × mv × p0 ,
где: mv - коэффициент относительной сжимаемости; р0 – дополнительное вертикальное давление в плоскости подошвы фундамента.
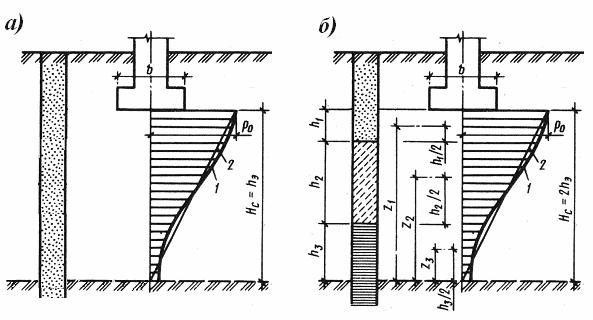
Рис. 71. Расчетная схема для определения осадок методом эквивалентного слоя в условиях однородного (а) и слоистого напластований (б):
1 – криволинейная эпюра дополнительных напряжений по оси фундамента; 2 – эквивалентная треугольная эпюра дополнительных напряжений по оси фундамента
В условиях слоистого напластования, мощность толщи грунтов, влияющую на осадки, принимают равной
Нс = 2 × hэ .
При расчете hэ необходимые для выбора Аω данные принимают для верхнего (первого) слоя грунта. В случае, если первый слой грунта тонкий (0,25·b и менее), то данные берутся по следующему, второму слою грунта. Если и второй слой грунта тонкий, то данные берутся по преобладающему напластованию. Криволинейную эпюру дополнительных напряжений по оси

118
фундамента заменяют на эквивалентную треугольную с вершиной на глубине 2·hэ (рис. 71 б). Осадку фундамента заданного размера и формы в
условиях слоистого напластования грунта определяют по формуле
s = hэ × mv × p0 ,
где mv – среднее значение коэффициента относительной сжимаемости.
Среднее значение коэффициента относительной сжимаемости определяют по формуле
|
|
1 |
n |
|
|
|
× åhi × mvi × zi , |
||
mv = |
||||
2 × h2 |
||||
|
|
э |
i=1 |
|
где: n – количество слоев в пределах сжимаемой толщи; hi – толщина i-го слоя грунта; mvi – коэффициент относительной сжимаемости i-го слоя грунта; zi – расстояние от точки, соответствующей глубине 2 · hэ до середины i-го слоя грунта.
Определение неравномерных осадок и крена фундамента проводят в случаях внецентренного нагружения фундамента.
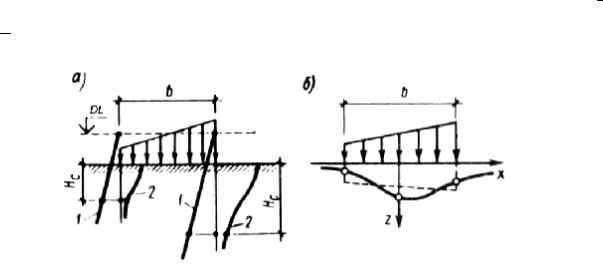
Для случая гибкого фундамента его неравномерную осадку можно найти, определив осадки, например, под центром и по краям приложения нагрузки (рис. 72 а). Учет жесткости фундамента производится путем проведения прямой линии, как средней, между точками, характеризующими осадку фундамента, которая и будет соответствовать действительной осадке фундамента (рис. 72 б). Тангенс угла наклона подошвы фундамента при его неравномерной осадке будет являться креном i.
При определении крена абсолютно жесткого фундамента СНиП 2.02.01-
83* рекомендует пользоваться формулой |
|
|
|
|
|
||||
i = |
1- v2 |
×k |
e |
× |
N ×e |
|
|||
E ×km |
æ a |
ö2 , |
|||||||
|
|
|
|||||||
|
|
|
|
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
è 2 |
ø |
|
||
где: Е и v – модуль деформации и коэффициент Пуассона грунта основания; ke – табличный коэффициент, зависящий от формы фундамента, направления
119
действия момента и глубины сжимаемой толщи; N и е – вертикальная
составляющая равнодействующей всех нагрузок на фундамент на уровне подошвы и ее эксцентриситет; а – диаметр круглого или сторона прямоугольного фундамента, в направлении которого действует момент; km – табличный коэффициент, учитываемый при а ≥ 10 м и Е ≥ 100 кг/см2.
В случае слоистого напластования принимают средневзвешенные значения v
и E в пределах сжимаемой толщи.
Рис. 72. Расчетная схема для определения неравномерных осадок (а) и кренов фундаментов (б):
1 – эпюра природного давления; 2 – эпюра дополнительного давления от сооружения; 3 – график значений неравномерных осадок; пунктирная линия – действительная осадка
абсолютно жесткого фундамента
В инженерной практике применяют и другие методы определения осадок фундаментов – метод линейно-деформируемого слоя, метод ограниченной сжимаемой толщи и др.
9.4. Практические методы расчета осадок оснований во времени
В случае залегания в основании фундамента водонасыщенных глинистых грунтов, его осадка может развиваться в течение длительного периода времени. В большинстве случаев процесс развития осадок во времени связан
с очень малой скоростью фильтрации воды в глинистых грунтах и вследствие этого медленным уплотнением глинистых грунтов (фильтрационной консолидацией). К осадкам, происшедшим вследствие консолидации
