Учебное пособие. Механика грунтов

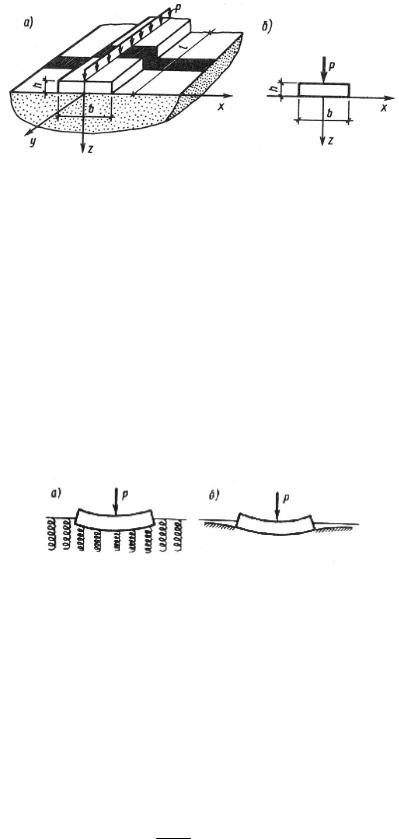
60

p(x)= k × w(x), где k – коэффициент пропорциональности (постели).

Рис. 36. Схема балки (а) и расчетная схема для случая плоской задачи (б)

Схема деформирования основания в модели местных упругих деформаций показана на рис. 37 а. Видно, что осадка поверхности основания за пределами фундамента отсутствует (фундамент стоит как бы на отдельных пружинах). Модель местных упругих деформаций хорошо применима для расчетов фундаментов на сильносжимаемых грунтах (Е ≤ 5 МПа), на лессовых просадочных грунтах, а также на ограниченной толще сжимаемых грунтов, лежащих на несжимаемом основании (скальном грунте).

Рис. 37. Деформации поверхности основания:

а – модель местных упругих деформаций; б – модель упругого полупространства

В модели упругого полупространства поверхность грунта оседает как в пределах, так и за пределами площади загрузки (рис. 37 б), причем кривизна

прогиба зависит от механических свойств грунтов и мощности сжимаемой толщи в основании. В случае плоской задачи прогиб поверхности под

действием нагрузки Р описывается уравнением w(x)= πP×C ×ln(x - ξ )+ D ,

61

где: С – коэффициент жесткости основания; х – координата точки поверхности, в которой определяется осадка; ξ – координата точки приложения силы Р; D – постоянная интегрирования.

Коэффициент жесткости основания С определяется как

С = 1 −Еν2 ,

где: Е – модуль деформации основания; ν – коэффициент Пуассона.

Существенным недостатком модели упругого полупространства является то, что в ней не ограничивается мощность сжимаемой толщи, поэтому данная

модель применима при расчетах фундаментов не слишком большой площади на достаточно плотных грунтах. Для сооружений с площадью опирания в

десятки и сотни квадратных метров более приемлема модель упругого слоя ограниченной мощности.

Контактные напряжения на подошве центрально-загруженных абсолютно жестких фундаментов определяют исходя из того, что вертикальные

перемещения в любой точке поверхности грунта на уровне подошвы одинаковы, т.е. w(x, y) = const.

Для круглого в плане фундамента (пространственная задача) контактные

напряжения можно определить как

ρ – расстояние от центра фундамента до точки, в которой определяется ордината p(ρ).

Для полосового фундамента в случае плоской задачи контактные напряжения можно определить как

где: х – расстояние от середины фундамента до точки, в которой определяется ордината p(х); а = b/2 – половина ширины подошвы фундамента.

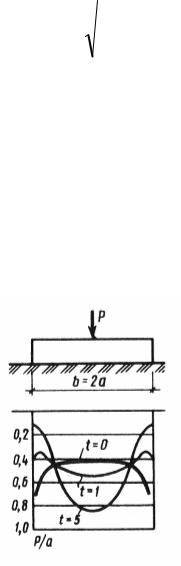
Гибкость фундамента оказывает влияние на характер эпюры контактных напряжений. На рис. 38 показано три эпюры распределения контактных напряжений в зависимости от показателя гибкости фундамента t (t = 0 – абсолютно жесткий фундамент).

Рис. 38. Эпюры контактных напряжений под фундаментом при различном показателе

гибкости

Неравномерное распределение контактных напряжений у жестких и гибких фундаментов заметно лишь в верхней части основания, на глубине около b/2 от подошвы. Общая форма распределения напряжений у жестких и гибких фундаментов различается незначительно, вследствие чего общая осадка фундаментов мало зависит от их жесткости, что позволяет вводить упрощения. Однако, осадка абсолютно жестких фундаментов несколько меньше, чем у гибких.

63

Достоверное знание контактных напряжений необходимо для расчетов конструкций фундаментов. Для расчетов напряжений в грунтах основания допускается упрощенное определение контактных напряжений.

Для центрально-нагруженного фундамента принимают равномерное

распределение напряжений по подошве

p = PA ,

где: Р – сила; А – площадь фундамента.

Для случая плоской задачи, при нагружении фундамента силой Р и моментом М, краевые значения контактных напряжений определяют как

pmax = P ± M , где: W – момент сопротивления подошвы фундамента.

min A W

Распределение контактных напряжений будет иметь линейный характер между значениями рmin и рmax.

5.3. Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности

Основное практическое значение имеет расчет напряжений для случаев плоской, пространственной и осесимметричной задач. Грунты основания в расчетах рассматриваются как упругое полупространство, распределение напряжений в грунтах основания определяется методами теории упругости.

Полученные методами теории упругости напряжения соответствуют стабилизированному состоянию, когда внешняя нагрузка полностью уравновешена внутренними силами (эффективными напряжениями в грунте). Зонами развития пластических деформаций, возникающими в грунтах основания по краям фундаментов пренебрегают.

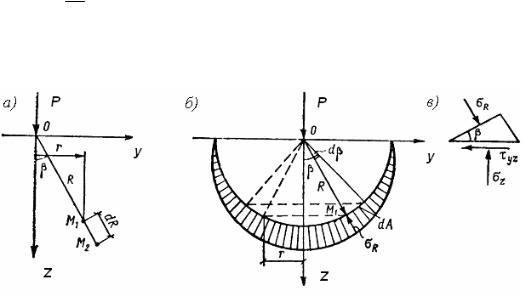
Рассмотрим действие вертикальной сосредоточенной силы Р, приложенной в т. О к горизонтальной плоскости, являющейся поверхностью линейно-деформируемого полупространства, простирающегося в

64

бесконечность ниже этой плоскости (рис. 39 а). Под действием силы Р во всех точках полупространства возникает сложное напряженное состояние. В общем случае в каждой точке полупространства, удаленной от т. О, в декартовой системе координат будет действовать шесть составляющих σx, σy, σz, τxy, τyz и τzx. Решение этой задачи было выполнено в 1885 г. Буссинеском и данная задача получила название задачи Буссниеска.

Пусть положение т. М1 (рис. 39 а) определяется от т. О полярными координатами R и β. Под действием силы Р т. М1 переместится в направлении R на величину s1. Причем при R = ∞ s1 = 0. Следовательно, значение s1 будет обратно пропорционально значению R. Также, при одинаковом значении R и различных значениях угла β, значения перемещений s1 будут различаться, причем значение s1 = max будет иметь место на оси Z при β = 0, а на поверхности грунта при β = 900 значение s1 = 0.

Следовательно

s1 = αR1 ×cos β , где α1 – коэффициент пропорциональности.

Данная зависимость удовлетворяет граничным условиям.

Рис. 39. Схема к выводу формулы:

а – расположение т.т. М1 и М2 в пространстве; б – распределение напряжений по полушаровой поверхности с радиусом R; в – напряжения, действующие в т. М1

Рассмотрим т. М2, находящуюся на продолжении радиуса R и расположенную на расстоянии dR от т. М1 (рис. 39 а). Перемещение т. М2 по направлению R будет равно

Относительная деформация грунта на отрезке dR будет равна

Если пренебречь величиной R · dR, много меньшей R, и учесть линейную зависимость между напряжениями и деформациями, то можно записать уравнение для сжимающих напряжений, действующих на площадки, перпендикулярные направлению радиуса R, без учета силы тяжести грунта

где α2 – коэффициент пропорциональности между напряжениями и деформациями.

Для нахождения α1 · α2 отсечем часть полупространства полушаровой поверхностью с центром в т. О и радиусом R (рис. 39 б). Составим уравнение равновесия проекций на вертикальную ось Z всех сил, действующих на отсеченный элемент, для невесомой среды

где dA – площадь кольца полушаровой поверхности при изменении угла β на величину dβ.

Подставляя в уравнение (б) значение σR, определенное по выражению (а) и решая его, найдем произведение коэффициентов α1 · α2. После подстановки

Напряжение σR действует на наклонную площадку элементарной призмы (рис. 39 в). Составим уравнение проекций всех сил на вертикальную ось Z

66

σz ×dA - σR ×cos β ×dA = 0 .

cos β

Подставив в полученное уравнение значение σR по выражению (в), определим вертикальное напряжение, принимаемое при сжатии с

положительным знаком

σz = 23×π × RP2 ×cos3 β .

Учитывая, что cos β = z/R (рис. 5 а), получим

Учитывая, что R2 = r2 + z2, получим

σz = zK2 × P ,

где К – табличное значение, зависящее от отношения r/z

Аналогично могут быть определены и все остальные пять компонентов напряжения в т. М1.

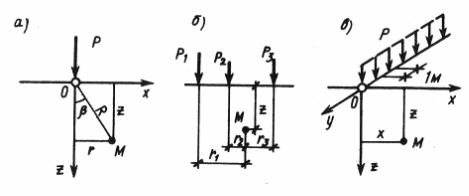
Наибольший практический интерес при расчетах осадок фундаментов представляют вертикальные сжимающие напряжения σz. Основные расчетные схемы для определения σz показаны на рис. 40.

Для случая действия нескольких сосредоточенных сил Рi, вертикальное сжимающее напряжение σz в любой точке упругого полупространства М (рис. 40 б), используя принцип суперпозиции, будет равно

67

Рис. 40. Расчетные схемы определения напряжений:

а – задача Буссинеска; б – задача о действии нескольких сил; в – задача Фламана

Для случая действия вертикальной сосредоточенной силы Р в условиях плоской задачи, приложенной к поверхности упругого полупространства,

Фламаном были определены все компоненты напряжений в любой точке полупространства М (рис. 40 в) в виде

Таким образом, зная закон распределения нагрузки на поверхности в пределах контура нагружения, можно, интегрируя задачу Буссинеска,

определить точные значения напряжений в любой точке грунтов основания для осесимметричной и пространственной нагрузки, а интегрируя задачу Фламана – для случая плоской нагрузки.

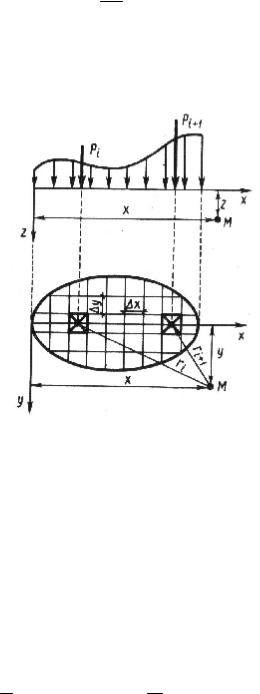
Используя задачи Буссинеска и Фламана можно найти приближенные значения напряжений в любой точке основания при любой форме фундамента и заданном законе распределения нагрузки методом элементарного суммирования. Пусть на поверхности упругого

полупространства в пределах сложного контура действует некоторая распределенная нагрузка (рис. 41). Разобьем контур нагружения на i

элементарных фигур и заменим в пределах каждой элементарной фигуры распределенную нагрузку соответствующей сосредоточенной силой Рi = p(x,y)· x· y. Тогда для определения σz в любой точке упругого

68

полупространства М, находящейся на глубине z, можно, используя принцип суперпозиции, воспользоваться формулой

σz = z12 × ån Ki × Pi . i=1

Аналогично можно определить все компоненты напряжений и в условиях плоской задачи.

Рис. 41. Схема к приближенному расчету напряжений в любой точке основания

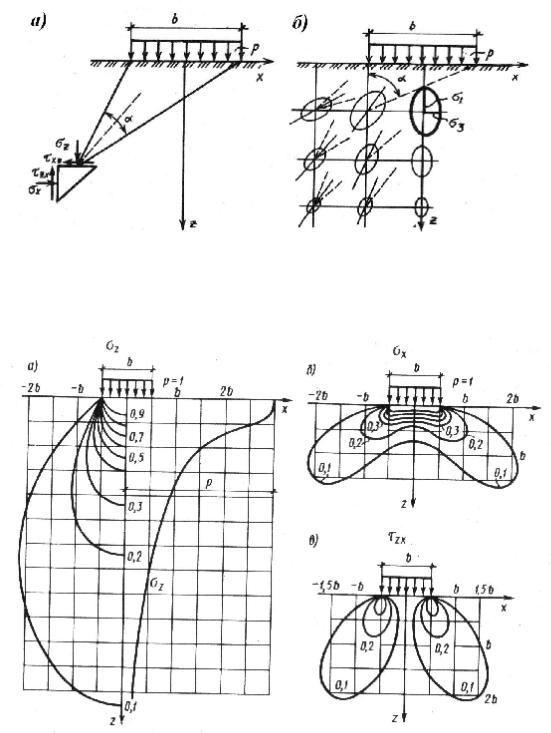
Для случая действия равномерно распределенной нагрузки интенсивностью р в условиях плоской задачи, приложенной к поверхности упругого полупространства, Колосовым были определены точные значения компонент напряжений в любой точке полупространства (рис. 42 а) в виде

σz = Kz × p ; σx = Kx × p ; τxz = Kxz × p ,

σm = 31 ×(σx + σy + σz )= 3p ×(Kx + Kz )×(1- ν).

Коэффициенты влияния Кz, Кx, Кxz определяются по приложению В, в зависимости от отношения x/b и z/b, где: x и y – координаты точки, в которой определяются напряжения; b – ширина полосы загружения.