Учебное пособие. Механика грунтов

130

10.4. Методы решения задач нелинейной механики грунтов. Методы переменной жесткости, начальных напряжений, начальных деформаций

Решение физически нелинейных задач механики грунтов выполняется специальными способами, сводящимися к итерационным процессам вычислений. Итерационный процесс представляет собой последовательное выполнение приближений (итераций). В случае линейной зависимости между напряжениями и деформациями грунта, его деформационные свойства определяются постоянными значениями модулей объемной деформации K и сдвига G, и решение системы уравнений МКР и МКЭ позволяет получить окончательный результат в первом приближении (итерации). Для случая

физически нелинейного материала выполняется последовательность итераций, но для каждой итерации проводят анализ напряженно- деформированного состояния в узлах (для МКР) или в элементах (для МКЭ), и система уравнений преобразуется таким образом, чтобы выполнялись нелинейные соотношения между напряжениями и деформациями, а также условия равновесия. Итерационный процесс заканчивается при достижении необходимой точности решения.

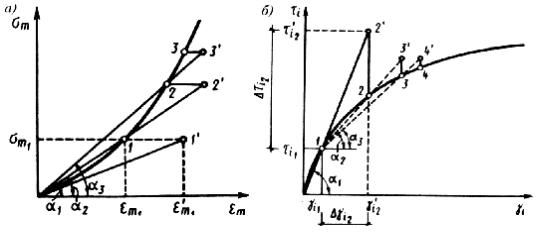
Метод переменной жесткости можно рассмотреть на примере задачи о расчете напряженно-деформированного состояния грунтового массива, в предположении, что массив грунта однороден и его механические свойства описываются диаграммами объемного сжатия и изменения формы, которые определены экспериментально. Решение задачи осуществляется последовательным выполнением итераций. В каждой итерации грунтовый массив рассматривается в виде линейно-деформированного тела с фиксированными для данной итерации значениями K и G. В качестве начальных значений K и G часто принимают наклон начальных участков, например, на рис. 78 а начальное значение K1 принимается равным tg α1. Аналогично назначается и значение G1. После выполнения первой итерации

131

получают определенные значения напряжения σm и деформации εm, причем точки, соответствующие данным значениям, в соответствии с законом линейного деформирования, окажутся на луче, проведенном под углом α1 к оси εm, и будут отклоняться от реального графика εm = f(σm). Пусть для некоторого элемента была получена точка 1' c координатами ε'm1 и σm1. Сохраняя постоянным значение σm1, точка 1' смещается до графика εm = f(σm) в положение 1 и определяется новое значение модуля K2, который часто называют секущим модулем. Далее проводится повторное решение задачи (вторая итерация) с полученным значением K2 и определяется для рассматриваемого элемента точка 2', которая будет лежать уже несколько ближе к графику εm = f(σm). После вышеуказанной корректировки получают значение K3 и в результате третьей итерации точку 3'. Дальнейшие решения проводятся аналогично до достижения необходимой точности решения.

Рис. 78. Схемы решения нелинейных задач методом переменной жесткости (а)

ипри инкрементальном нагружении (б)

Вслучае необходимости учета последовательности приложения нагрузок (разгрузка основания при разработке котлована, поэтапное нагружение при возведении сооружения и др.) при проведении расчета нагрузка прикладывается отдельными шагами (инкрементами) { F}, т.е. осуществляется инкрементное нагружение, и на каждом шаге выполняется итерационное решение нелинейной задачи. В результате на каждом шаге определяются не полные перемещения {U}, а их приращения { U}. В

132

качестве примера рассматривается график изменения формы (рис. 78 б). Пусть начальное значение модуля сдвига характеризуется величиной G1, равной tg α1, и после первого нагружения { F1} в некотором элементе получено напряженно-деформированное состояние, соответствующее точке 1 с координатами γi1 и τi1. При этом определены векторы перемещений {U1}, деформаций {ε1} и напряжений {σ1}. После проведения первой итерации при значении G1, определяются приращения векторов перемещений { U'2}, деформаций {Δε'2} и напряжений {Δσ'2}, через которые вычисляются полные значения напряжений и деформаций, а затем сдвиговые деформации γ'i2 и напряжений τ'i2. Точка 2' будет соответствовать γ'i2 и τ'i2. Поскольку точка 2' отклоняется от реального графика γi = f(τi), проводится итерационный процесс, аналогичный описанному выше, с той разницей, что цепь итераций выполняется для каждого инкремента нагружения. В следующих итерациях назначаются модули сдвига, соответствующие тангенсам углов α2, α3 и т.д. и называемые касательными (тангенциальными) модулями.

Недостатком вышеизложенных итерационных процессов является необходимость в каждой итерации заново формировать систему уравнений, поскольку изменяются параметры деформационных свойств, и производить ее обращение для получения промежуточных решений, что требует больших временных затрат. Существенно сократить время выполнения расчетов позволяют метод начальных напряжений и метод начальных деформаций.

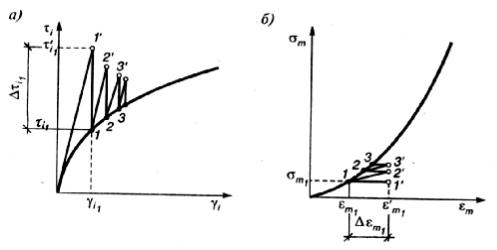
В методе начальных напряжений итерационный процесс сопровождается изменением вектора нагрузки. После получения упругого решения (точка 1' на рис. 79 а) определяется отклонение полученных значений напряжений от реальных Δτi1. Полученная разность перераспределяется в соответствии с упругим законом в узлы элемента в виде узловых сил, которые добавляются к вектору нагрузки. Последующая итерация выполняется с измененным вектором нагрузки без дополнительной модификации системы уравнений.

133

Метод начальных деформаций схож с методом начальных напряжений,

но по данному методу после получения упругого решения определяется отклонение вычисленных деформаций от реальных Δεm1. Полученное отклонение (рис. 79 б) в соответствии с упругим законом пересчитывается в

соответствующий дефицит напряжений с дальнейшим преобразованием в дополнительные узловые силы.

Рис. 79. Схемы решения нелинейных задач методом начальных напряжений (а)

иметодом начальных деформаций (б)

Вцелом в методе начальных напряжений и методе начальных деформаций, при общей экономии времени на проведение одной итерации, возрастает количество итераций. Метод начальных напряжений целесообразно применять для выполаживающихся графиков, а метод начальных деформаций – для восходящих графиков.

10.5.Реализация численных методов расчета на ЭВМ

Метод конечных разностей может успешно использоваться для решения задач фильтрации и теории упругости. Однако МКР имеет и недостатки, такие, как невозможность локального сгущения сетки численного

интегрирования и сложность решения для неоднородных областей и нелинейных сред. Метод конечных элементов способен реализовать конечно-

134

разностный процесс численного интегрирования для нерегулярных сеток и неоднородных областей, и является в настоящее время основным методом численного анализа в геомеханике.

Даже поверхностное знакомство с численными методами показывает, что

решение задач сопровождается обработкой огромных объемов числовой информации, связанной с необходимостью формирования и решения систем уравнений с большим числом неизвестных, что возможно только с применением высокопроизводительных ЭВМ. Важной особенностью численных методов является то, что определенные способы решений однотипны для различных задач и приложений методов. Эти способы могут

быть описаны стандартными алгоритмами и оформлены в виде самостоятельных подпрограмм. В таким случае функции основной

программы в основном сводятся к управлению вызовом из библиотеки нужных подпрограмм в соответствии с постановкой и выбранным методом решения краевых задач.

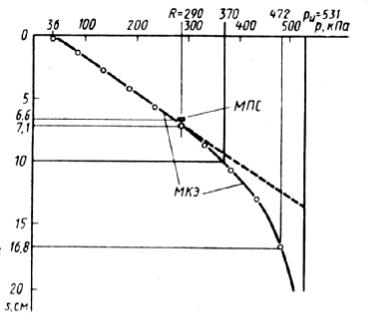
Преимущества численных методов расчета представлены на примере расчета осадки некоторого фундамента методом послойного суммирования МПС и методом конечных элементов (рис. 80). При помощи МПС может быть определена только одна точка, соответствующая осадке s = 6,6 см при давлении под подошвой фундамента p = R = 290 кПа. При помощи МКЭ можно получить полный график зависимости s = f(p). Из графика видно, что при давлениях под подошвой фундамента, не превышающих значение природного давления грунта (γ·d = 36 кПа), осадки отсутствуют, поскольку

они прикладываются к уже имеющемуся уплотнению от собственного веса грунта. Также заметно, что при p = R осадка, полученная при помощи МКЭ (s = 7,1 см) несколько больше осадки, полученной при помощи МПС (s = 6,6 см), что объясняется учетом в МКЭ влияния на осадку бокового расширения грунта. Последнее устойчивое значение осадки s = 16,8 см было получено при р = 472 кПа, далее итерационный процесс расходился, что

135

свидетельствовало о достижении грунтом предельного состояния. Наиболее

экономичные размеры фундамента могут быть получены при s = su = 10 см, причем в данном случае значение р, соответствующее s = 10 см будет превышать R и расчет осадки по МПС будет невозможен. Однако, если принять s = 10 см и по графику s = f(p), построенному при помощи МКЭ, определить соответствующее значение р = 531 кПа, при котором размеры фундамента будут наиболее экономичными, то экономия, например, только в расходе железобетона составит 20 %.

Рис. 80. Расчетные осадки, полученные МПС и МКЭ

В настоящее время круг практических задач, решаемых численными методами, постоянно расширяется. Разработаны мощные программные комплексы, решающие геотехнические задачи при помощи МКЭ, такие, как "Лира" (НИИАС, Киев), "Геомеханика" (СПбГАСУ, С-Петербург), "FLAC" (ITASCA, США), "PLAXIS" (PLAXIS, Голландия) и др. Современные

программные комплексы позволяют моделировать весь ход строительства объекта, вводить модели тонких конструкций (анкеров, подпорных стенок и т.п.), рассчитывать поровое давление, температурные поля и изменение свойств грунтов при замерзании – оттаивании.

136

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Цытович, Н.А. Механика грунтов (краткий курс) [Текст]: Учебник для строит. вузов. - М.: Высш. шк., 1983.

2.Далматов, Б.И. Механика грунтов, основания и фундаменты (включая специальный курс инженерной геологии) [Текст]. - Л.: Стройиздат, 1988.

3.Механика грунтов, основания и фундаменты [Текст]: Учеб. пособие для строит. спец. вузов / С.Б. Ухов, В.В. Семенов, В.В. Знаменский и др.; Под ред. С.Б. Ухова. - М.: Высш. шк., 2002.

4.Маслов, Н.Н. Механика грунтов в практике строительства (оползни и борьба с ними) [Текст]: Учеб. пособие для вузов. - М.: Стройиздат, 1977.

5.ГОСТ 5180-84. Грунты. Методы лабораторного определения физических характеристик [Текст].

6.ГОСТ 12248-96. Грунты. Методы лабораторного определения характеристик прочности и деформируемости [Текст].

7.ГОСТ 12536-79. Грунты. Методы лабораторного определения гранулометрического (зернового) и микроагрегатного состава [Текст].

8.ГОСТ 23161-78. Грунты. Метод лабораторного определения характеристик просадочности [Текст].

9.ГОСТ 23740-79. Грунты. Методы лабораторного определения содержания органических веществ [Текст].

10.ГОСТ 24143-80. Грунты. Методы лабораторного определения характеристик набухания и усадки [Текст].

11.ГОСТ 25100-95. Грунты. Классификация [Текст].

12.ГОСТ 25584-90. Грунты. Методы лабораторного определения коэффициента фильтрации [Текст].

13.СНиП 2.02.01-83* Основания зданий и сооружений [Текст].

Расчетные сопротивления глинистых непросадочных грунтов

138

Приложение Б

(справочное)

Значения статистического критерия v при двусторонней доверительной вероятности α = 0,95

Приложение В

(справочное)

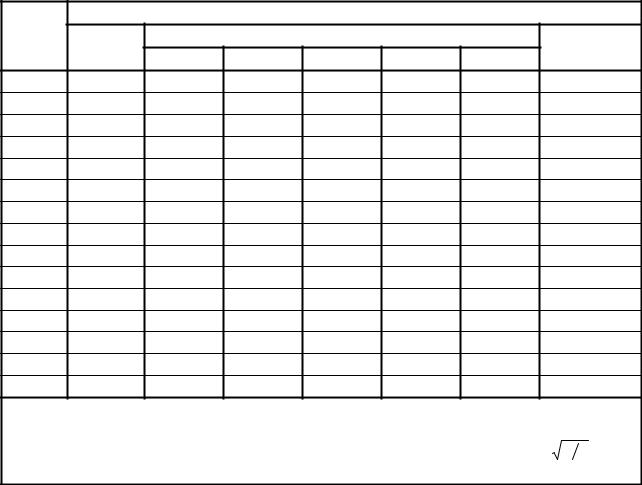
Значения коэффициентов влияния Kz, Kx, Kxz