
Учебное пособие. Механика грунтов
.pdf100 |
|
|
|
σx = ξ × σz = ξ × γ × z = |
v × γ × z |
, |
|
1 - v |
|||
|
|
где: γ – удельный вес грунта; v – коэффициент Пуассона.
Эпюру давления на стенку при однородном грунте засыпки принимают в виде треугольника, равнодействующую эпюры давления покоя Е0 при высоте стенки h определяют как площадь треугольника
E0 = |
v ×γ × h2 |
|
|
. |
|
2 ×(1- v) |
||
Вслучае смещения стенки в сторону от засыпки на величину – иа, в грунте засыпки формируется поверхность скольжения, ограничивающая призму обрушения грунта (рис. 61 а). Давление, передаваемое призмой обрушения на грань стенки называют активным давлением, результирующую активного давления обозначают как Еа.
Вслучае смещения стенки в сторону грунта засыпки на величину ип, в грунте засыпки также формируется поверхность скольжения, ограничивающая призму выпирания грунта (рис. 61 в). При этом реакция грунта соответствует пассивному давлению (отпору) грунта, результирующую пассивного давления обозначают как Ер.
Анализ графика на рис. 61 г показывает, что формирование призмы
обрушения и развитие Еа происходит при незначительных перемещениях стенки, и, наоборот, образование призмы выпирания и развитие Ер происходит при значительных перемещениях стенки.
Практически всегда активное давление действует со стороны грунта засыпки и стремится сдвинуть или повернуть стенку. Пассивное давление наоборот препятствует потере устойчивости стенки. Активное и пассивное давление определяют в соответствии с теорией предельного равновесия, и считают, что грунт в призме обрушения или выпирания находиться в состоянии предельного равновесия. Также в расчете используют допущение Кулона о прямолинейном очертании линий скольжения.

101
8.3. Аналитические методы определения активного и пассивного давления грунта
Рассмотрим простейший случай, когда засыпка представлена идеально сыпучим (φ ≠ 0, с = 0) грунтом (рис. 62). Примем, что стенка имеет абсолютно гладкую грань, следовательно, трение о стенку отсутствует τzx = 0. В таком случае вертикальные и горизонтальные площадки будут являться главными.
Рис. 62. Схема для определения активного давления сыпучего грунта на гладкую стенку
Максимальное главное напряжение, действующее на горизонтальную площадку в точке контакта грунта со стенкой на глубине z от поверхности засыпки будет равно σ1 = γ · z. Исходя из условия предельного равновесия для сыпучих грунтов, минимальное главное напряжение, действующее на
горизонтальную площадку в точке контакта грунта со стенкой будет равно
σ3 = σ1 ×tg |
2 |
æ |
- |
φ ö |
æ |
- |
φ ö |
||
|
ç45 |
2 |
÷ |
= γ × z ×ç45 |
2 |
÷ . |
|||
|
|
è |
|
ø |
è |
|
ø |
||
В соответствии с данной формулой, эпюра активного давления будет иметь вид треугольника с максимальной ординатой, равной
max |
= γ × h×tg |
2 |
æ |
- |
φ ö |
, где h – высота стенки. |
σа |
|
ç45 |
÷ |
|||
|
|
|
è |
|
2 ø |
|
Равнодействующую активного давления Еа можно определить как площадь эпюры σа (площадь треугольника)

|
|
102 |
|
|
|
|
|
|
|
γ ×h2 |
|
2 |
æ |
|
φ ö |
|
|
Еа = |
|
×tg |
|
ç45 |
- |
|
÷ |
, |
2 |
|
2 |
||||||
|
|
|
è |
|
ø |
|
||
которая будет приложена к стенке по центру тяжести площади эпюры σа на расстоянии h/3.
Плоскость скольжения призмы обрушения будет расположена под углом π/4 – φ/2 к вертикали, ширину призмы обрушения можно определить как
æ |
|
φ ö |
||
l = h ×tgç45 |
- |
|
÷ . |
|
2 |
||||
è |
|
ø |
||
При наличии на поверхности идеально сыпучего грунта сплошной равномерно распределенной нагрузки интенсивностью q (рис. 63 а), максимальное главное напряжение, действующее на горизонтальную площадку в точке контакта грунта со стенкой на глубине z от поверхности
засыпки будет равно
σ1 = γ × z + q .
Всоответствии с вышеизложенными решениями
σа |
= (γ × h + q)×tg |
2 |
ç45 - |
÷ |
, |
||||||
max |
|
|
|
æ |
|
|
|
φ ö |
|
||
|
|
|
|
|
|
è |
|
|
|
2 ø |
|
при h = 0 (поверхность грунта) |
|
|
|
|
|
|
|
|
|
|
|
|
min |
|
2 |
æ |
|
|
φ |
ö |
|
|
|
|
σа |
= q ×tg |
|
ç45 |
- |
|
÷ |
, |
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
è |
|
|
ø |
|
|
|
|
следовательно, эпюра активного давления будет иметь вид трапеции.
Равнодействующую активного давления Еа можно определить как площадь эпюры σа (площадь трапеции)
æ γ × h |
ö |
|
2 |
æ |
|
φ ö |
|
|
Еа = h ×ç |
|
+ q÷ |
×tg |
|
ç45 |
- |
÷ |
, |
2 |
|
|||||||
è |
ø |
|
|
è |
|
2 ø |
|
|
которая будет приложена к стенке по центру тяжести площади эпюры σа на расстоянии от подошвы стенки r, равном
r= h ×((γ ×h + 3×q)) .
3× γ ×h + 2 ×q
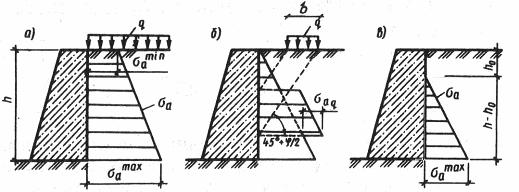
103
Рис. 63. Схемы для определения активного давления:
а– идеально сыпучий грунт при наличии равномерно распределенной нагрузки;
б– идеально сыпучий грунт при наличии местной нагрузки; в – связный грунт
При наличии на поверхности идеально сыпучего грунта местной нагрузки интенсивностью q и шириной b (рис. 63 б), считают, что воздействие нагрузки на стенку будет передаваться под углом π/4 + φ/2 к горизонтали. В
пределах определенной данным образом области воздействия к имеющейся эпюре активного давления добавляют активное давление σа,q, равное
|
2 |
æ |
|
φ ö |
|
σа,q = q ×tg |
|
ç45 |
- |
|
÷. |
|
2 |
||||
|
|
è |
|
ø |
|
Равнодействующую активного давления Еа можно определить как площадь полной эпюры, точка приложения Еа соответствует центру тяжести полной эпюры.
Для грунта, обладающего внутренним трением и сцеплением (φ ≠ 0, с ≠0), (рис. 63 в) условие предельного равновесия равно
|
2 |
æ |
|
φ ö |
æ |
|
φ ö |
||
σ3 = σ1 ×tg |
|
ç45 |
- |
|
÷ |
- 2 ×c ×tgç45 |
- |
|
÷ . |
|
|
|
|||||||
|
|
è |
|
2 ø |
è |
|
2 ø |
||
В соответствии с вышеизложенными решениями
max |
= γ × h ×tg |
2 |
æ |
- |
φ ö |
æ |
- |
φ ö |
||
σа |
|
ç45 |
2 |
÷ |
- 2 ×c ×tgç45 |
2 |
÷ . |
|||
|
|
|
è |
|
ø |
è |
|
ø |
||
При построении эпюры активного давления необходимо учесть, что связный грунт способен удерживать вертикальный откос высотой h0, равный:
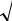
104
h = 2 ×c ×cos φ |
= |
||||
0 |
|
|
|
|
|
γ × |
(1 |
- sin φ) |
|
||
|
|
||||
2 ×с
|
|
|
|
|
æ |
|
φ ö , |
||
γ ×tgç45 |
- |
|
÷ |
|
|
||||
è |
|
2 ø |
|
|
следовательно, в пределах h0 от свободной поверхности засыпки связный грунт не будет оказывать давления на стенку. Равнодействующую активного давления Еа можно определить как площадь треугольной эпюры высотой h – h0 c максимальной ординатой σmaxа, точка приложения Еа соответствует центру тяжести данной эпюры.
Учет нагрузки на поверхности засыпки связного грунта проводят в соответствии с вышеизложенными решениями.
Учет наклона, шероховатости задней грани стенки и наклона поверхности засыпки является достаточно общим случаем. Рассмотрим предельное состояние призмы обрушения ОАВ согласно расчетной схеме, представленной на рис. 64 а. На призму обрушения будут действовать собственный вес грунта Pg, реактивный отпор массива грунта R ниже поверхности скольжения АВ и реактивный отпор стенки Еа. Реактивный отпор стенки Еа можно определить, зная значение Pg, углы направления
остальных усилий и построив треугольник сил относительно некоторого значения угла наклона поверхности скольжения Θ (рис. 64 б). Используя правило экстремума dEa/dΘ = 0, можно получить значение Еа, равное
Ea = |
γ × h2 |
|
|
× |
cos2 |
(φ - ε) |
||
|
|
|
|
|
|
|||
2 ×(1+ |
z )2 |
cos2 ε ×cos(ε + ω), |
||||||
|
|
|||||||
где: φ – угол внутреннего трения грунта; ε – угол наклона задней грани стенки к вертикали; α – угол наклона поверхности засыпки к горизонтали (+ соответствует восходящей, – соответствует нисходящей засыпке); ω – угол
отклонения равнодействующей Еа от нормали к стенке за счет трения грунта о стенку (для стенок с повышенной шероховатостью равен φ, для
мелкозернистых водонасыщенных песков и при вибрационных нагрузках ω = 0, в остальных случаях ω = 0,54·φ).
105
Рис. 64. Схема действия сил на стенку с шероховатой наклонной гранью (а) и треугольник равнодействующих сил (б)
Значение z принимают по формуле
= sin(φ + ω)× sin(φ - α) z cos(ε + ω)×cos(ε - α).
Данное решение неприменимо в случае крутого откоса (при α > φ), который сам по себе неустойчив, и для стенок с очень пологой задней гранью (при ε > 65-700). При более сложных случаях применяют другие методы, в частности графический метод Кульмана, позволяющий решать задачи при произвольном очертании поверхности засыпки и любых схемах загружения.
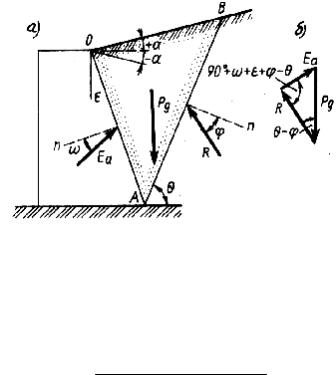
Определение активного давления при ломаной форме задней грани стенки и неоднородных грунтах засыпки производится путем разбиения стенки и грунтов засыпки на отдельные участки, в пределах которых угол наклона стенки и физико-механические характеристики грунтов постоянны. Также учитывают взвешивающее действие воды (рис. 65). Построение эпюры
активного давления начинают с верхнего участка стенки в соответствии с приведенными выше решениями. Влияние вышерасположенных грунтов
засыпки при определении активного давления в пределах нижерасположенного участка учитывается как равномерно распределенная нагрузка q.
106
Рис. 65. Построение эпюры активного давления при ломаной форме задней грани стенки и
неоднородных грунтах засыпки
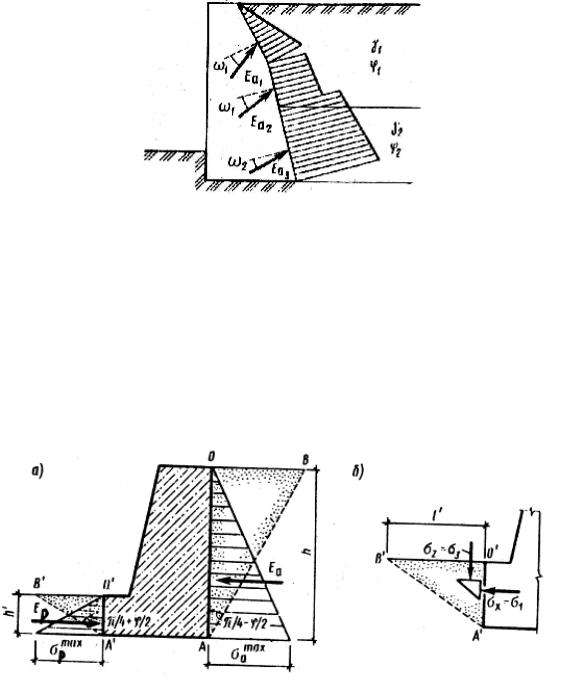
Пассивное давление возникает при перемещении стенки в сторону грунта засыпки (рис. 66). В данном случае главные напряжения меняются: σz = σ3 = γ·z при отсутствии пригрузки будет минимальным главным напряжением; а σx = σ1 = σp будет максимальным главным напряжением (рис. 66 б).
Рис. 66. Схема действия активного и пассивного давления на стенку
Следовательно, условие предельного равновесия для сыпучих и связных грунтов примет вид, соответственно
σ1 = σ3 ×tg |
2 |
æ |
+ |
φ ö |
и σ1 = σ3 ×tg |
2 |
æ |
+ |
φ ö |
æ |
+ |
φ ö |
|
|
ç45 |
2 |
÷ |
|
ç45 |
÷ |
+ 2 ×c ×tgç45 |
÷ . |
|||||
|
|
è |
|
ø |
|
|
è |
|
2 ø |
è |
|
2 ø |
|
Значения максимальных ординат пассивного давления для сыпучих и связных грунтов будут равны, соответственно
107
max |
|
2 |
æ |
|
φ ö |
max |
|
2 |
æ |
|
φ ö |
æ |
|
φ ö |
|||
σ p |
= γ × h'×tg |
|
ç45 |
+ |
|
÷ |
и σP |
= γ × h'×tg |
|
ç45 |
+ |
2 |
÷ |
+ 2 ×c ×tgç45 |
+ |
2 |
÷ . |
|
2 |
|
|||||||||||||||
|
|
|
è |
|
ø |
|
|
|
è |
|
ø |
è |
|
ø |
|||
Плоскость скольжения призмы выпирания будет выходить из т. А' под углом π/4 + φ/2 к вертикали, ширину призмы выпирания можно определить как
æ |
+ |
φ ö |
|
l' = h'×tgç45 |
2 |
÷ . |
|
è |
|
ø |
|
Далее, повторяя предыдущие решения, можно определить значение равнодействующей пассивного давления Ep и точку ее приложения к поверхности стенки.
Погрешность вышеизложенного расчета по определению пассивного давления возрастает с увеличением угла внутреннего трения грунта. При φ ≤ 100 погрешность удовлетворительна, при больших значениях φ следует использовать строгие решения теории предельного равновесия.
8.4. Определение активного и пассивного давления грунта строгими решениями теории предельного равновесия
Строгие решения теории предельного равновесия получены Соколовским для случая горизонтальной поверхности засыпки однородным сыпучим грунтом. Ординаты эпюр активного и пассивного давления можно
определить по формулам
|
|
|
|
|
σа = |
|
× (γ × z + q) и σ р = |
|
× (γ × z + q), |
|
|
|
|
|
q |
q' |
|||
где: |
|
q |
– интенсивность пригрузки на поверхность засыпки; |
||||||
|
|
и |
|
|
– безразмерные коэффициенты, принимаемые по приложению Л в |
||||
|
q |
q' |
|||||||
зависимости от угла внутреннего трения грунта φ, угла наклона грани стенки к вертикали ε и угла трения грунта о стенку ω (см. рис. 65).
Далее строят по полученным σа и σр эпюры активного и пассивного давления и определяют значения равнодействующих Еа и Ер как площади соответствующих эпюр.
108
9. ДЕФОРМАЦИИ ОСНОВАНИЙ И РАСЧЕТ ОСАДОК СООРУЖЕНИЙ
9.1. Значение вопроса. Основные положения. Виды деформаций оснований и сооружений
В ходе строительства сооружения, даже при условии обеспечения прочности грунта, возникают деформации основания. Как правило, они
имеют неравномерный характер и вызывают перераспределение усилий в конструкциях сооружения, что, в свою очередь может затруднить нормальную эксплуатацию здания и даже привести к аварии. Прогнозирование деформаций системы "сооружение-основание" представляет одну из наиболее сложных задач механики грунтов.
Под абсолютными перемещениями понимают осадку основания отдельного фундамента s и горизонтальное перемещение фундамента или сооружения u. К относительным перемещениям относят средние осадки основания сооружения, относительную разность осадок двух фундаментов, крен фундамента и т.д. Относительные деформации можно найти, зная абсолютные значения перемещений.
Расчет оснований по деформациям производят по условию s ≤ su, где: s – деформация, определенная расчетом; su – предельное значение, устанавливаемое нормативным документом или проектом.
Важнейшей предпосылкой многих методов расчета деформаций оснований является ограничение среднего давления под подошвой фундамента условием p ≤ R, что позволяет использовать математический аппарат теории линейного деформирования. Процесс строительства
рассматривается как одноразовое нагружение грунтов основания нагрузкой p, вызывающей их общее деформирование без разделения на упругую и пластическую составляющие. В ряде случаев может возникнуть
109
необходимость оценки деформаций оснований при p > R. Подобные задачи решаются при помощи нелинейной механики грунтов.
Другой важной предпосылкой является введение понятий стабилизированных и нестабилизированных деформаций. В основном
практический интерес представляют только наибольшие конечные стабилизированные перемещения, однако в ряде случаев возникает
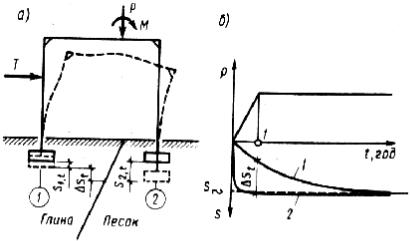
необходимость прогноза развития этих перемещений во времени (нестабилизированные), который выполняют в соответствии с теорией фильтрационной консолидации грунтов. Например, на рис. 67 показан случай, когда основание сооружения сложено различными грунтами.
Существенное различие времени развития деформаций в различных грунтах основания, даже при их равных стабилизированных деформациях, может привести на каком-либо этапе строительства или эксплуатации сооружения к превышению разности осадок фундаментов si предельных значений su и, как следствие, аварии сооружения.
Рис. 67 . Схема сооружения (а) и график развития осадок фундаментов (б) во времени: 1 – глина; 2 – песок
9.2. Теоретические основы расчета стабилизированных осадок
Постановка задачи расчета осадок фундаментов аналогична рассмотренной выше в п. 5.1. В случае центрально-нагруженного
