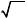Окороков Фракталы в фундаменталной физике.Фракталные свойства множественного образования частиц и топология выборки 2009

ляющаяся ядром интегрального преобразования [347].

Ядро может иметь в области интегрирования сингулярные точки, и тогда интеграл (П7.1) понимается в каком-либо специальном смысле (например, в смысле главного значения). Явные выра-

жения обратного преобразования U 1 z , позволяющие вос-

станавливать по функции распределение (функцию распределения F или плотность p ), называются формулами обращения. Примерами интегральных преобразований являются многомерные

лярное произведение n мерных векторов переменных:

1)преобразование Фурье – Стилтьеса (характеристический функционал) z,u exp i z,u ;

2)преобразование Лапласа – Стилтьеса на Rn (производящий функционал) z,u exp z,u ;

иследующие одномерные n 1 преобразования:

3)преобразование Меллина – Стилтьеса

0, u 0,

z,u us , u 0;

4) преобразование Ганкеля

где J – функция Бесселя;

5) косинус / синус преобразование

0, u 0,

z,u

cos/sin su , u 0.

Ниже более подробно рассмотрены интегральные преобразования играющие важную роль для физических приложений, рассмотренных в данной книге.

428

П7.1. Преобразование Фурье

В 1807 г. Ж. Фурье сформулировал круг идей, вошедших в современную математику под названием «ряды Фурье». Возникновение фурье-анализа стимулировало исследования в области основ математического анализа. В данном разделе основное внимание сфокусировано на основных идеях и теоремах данного раздела математики, которые имеют непосредственное отношение к созданию алгоритма моделирования фрактального броуновского движения.

Пусть функция X t , t , абсолютно интегрируема на

смысле Лебега. Важно отметить, что класс рассматриваемых функций включает кусочно-непрерывные функции, удовлетворяющие следующему условию роста:

К данному классу, в частности, относится и фрактальное броуновское движение, имеющее компактный носитель, то есть заданное на конечном отрезке и равное нулю вне него.

Определение П7.1. Преобразованием Фурье введенной выше

При определенных условиях имеет место формула обращения – формула обратного преобразования Фурье

которая в физических приложениях описывает синтез некоторого сигнала X t из отдельных частотных составляющих (гармоник).

429

В литературе для прямого и обратного преобразования Фурье, могут использоваться следующие соответствующие обозначения:

FT X t ; X и FT 1 X ;t X t .

Из определения (П7.3) и формулы обращения (П7.4) можно получить:

d n Xn t i n FT 1 n X ;t . dt

Пусть функция X t – периодическая с периодом, равным еди-

нице. Тогда частоты будут кратны целым величинам n и операция «преобразование Фурье» в данном случае имеет следующий вид:

Величины X n называются коэффициентами Фурье, а формула

обращения в данном случае есть не что иное как ряд Фурье:

X t X n exp i2 nt .

n

Если период функции X t отличен от T 1, то всегда можно из-

менить масштаб независимой переменной t таким образом, чтобы рассматриваемая функция имела период равный единице.

шем рассмотрении предполагается конечной. По теореме Планшереля справедливо следующее равенство:

то есть полная энергия может быть вычислена как по временной, так и по частотной области.

430

Необходимо отметить, что если X t – вещественно значная

функция, то справедлива следующая цепочка равенств: X

П7.2. Преобразование Лапласа

Из общих определений интегральных преобразований, рассмотренных выше следует, что преобразования Фурье и Лапласа могут быть введены единым образом: заменяя в преобразовании Фурье частоту не некоторый комплексный параметр так, что i , можно автоматически получить преобразование Лапласа.

Определение П7.2. Преобразованием Лапласа введенной выше

При определенных условиях (непрерывность X t ) имеет место формула обращения – формула обратного преобразования Лапласа

Re c 0 и понимается в смысле главного значения, то есть как предел интеграла вдоль отрезка c iA,c iA при A . .

В литературе для прямого и обратного преобразования Лапласа, могут использоваться следующие соответствующие обозначения:

Из определения (П7.6) и формулы обращения (П7.7) можно получить:

431

Необходимо отметить важное отличие от фурье-преобразова- ния: зависимость от начальных условий в первой формуле (П7.8) возникает вследствие того, что преобразование Лапласа, в отличие от преобразования Фурье, начинается при начальном значении переменной (времени) t 0. Поэтому преобразование Лапласа является полезным при решении проблемы начальных условий.

Ниже в данном разделе более подробно рассматривается преобразование Лапласа в рамках теории вероятности.

Пусть – неотрицательная случайная величина с функцией

распределения вероятностей F x P x .

Определение 7.3. Преобразованием Лапласа функции

распределения вероятностей F x P x (или случайной ве-

личины ) называется функция [16]

определенная при Re 0 и аналитическая для Re 0. Предполагается, что точка нуль включена в область интегриро-

вания.

Теорема 7.1 (обращения). Функция распределения случайной величины F x P x однозначно определяется своим преоб-

разованием Лапласа : в каждой точке непрерывности функ-

ции распределения справедливо

432

Преобразование Лапласа можно представить в виде ряда

в любом интервале 0 0 , в котором указанный ряд сходится. Если такой интервал сходимости ряда существует, то последова-

тельность моментов mk k 0 однозначно определяет функцию рас-

пределения F x P x .

Важно отметить, что преобразование Лапласа при веще-

ственных 0 имеет вероятностный смысл:

F P , 0, (П7.11)

где – случайная величина, не зависящая от и характеризуемая функцией распределения: F t P t exp t с преобразо-

ванием Лапласа exp s s .

Соотношение (П7.11) в приложениях интерпретируется следующим образом: exp при 0 представляет со-

бой вероятность того, что момент успеха (восстановления, вызова, отказа и тому подобное) наступит до момента прекращения на-

блюдений , имеющего, в свою очередь, показательное распределение.

Если для случайной величины определена плотность распре-

деления вероятностей p x P x dF x dx, то преобразо-

вание Лапласа (П7.9) может быть записано в виде

exp exp x p x dx.

0

Формула обращения (П7.10) в данном случае имеет вид

и для почти всех x 0 справедливо

433

где c 0 и интеграл берется вдоль любой прямой Re c 0 и понимается в смысле главного значения, то есть как предел интеграла вдоль отрезка c iA,c iA при A .

Если плотность распределения p x непрерывна, то

и обозначается F F F [343].

П7.3. Обобщенные интегральные преобразования

Рассмотренные выше преобразования Фурье и Лапласа могут быть обобщены на случай дробных порядков [208].

Пусть функция X t удовлетворяет указанным выше условиям.

Учитывая обобщенную формулу Лейбница (2.33) и соотношение

можно получить:

Применяя преобразование Фурье для производной целого порядка, данное соотношение может быть переписано в виде

434

Функция

Полученное соотношение имеет важное значение. С одной стороны, оно позволяет вычислять производную дробного порядка с помощью некоторого интегрального преобразования без использования рядов. С другой стороны, данное соотношение, являясь аналогом (П7.5), позволяет определить, соответственно, прямое и обратное обобщенное преобразование Фурье следующим образом:

Действуя аналогично, а также используя формулу (П7.8) и формальное соответствие i , можно получить

и формально определить соответственно прямое и обратное обобщенное преобразование Лапласа следующим образом:

435

Однако в данном случае имеется фундаментальное отличие от обобщенного преобразования Фурье. В последнем случае сходимость определяется только формой функции, участвующей в преобразовании. С другой стороны, сходимость (стандартного / обобщенного) преобразования Лапласа дополнительно к форме преобразовываемой функции определяется сходимостью при t (стандартной / обобщенной) экспоненциальной функции. В отличие от стандартного случая, обобщенная экспонента E t спа-

дает не по экспоненциальному, а по обратному степенному закону в асимптотике t . Поэтому сходимость обобщенного преобразования Лапласа является не очевидным фактом и данный вопрос требует аккуратности и дополнительных исследований для конкретных функций X t [208].

436

УПРАЖНЕНИЯ

Упражнение 1.

Проверить, что требование справедливости равенства (4.1) равносильно требованию выполнения любого из следующих двух равенств:

а) t T, B F t почти наверное справедливо следующее соотношение P B F t P B F t ;

б) t T, B F t почти наверное справедливо следующее соот-

тоже является булевой полуалгеброй подмножеств множества . Показать, что булева алгебра ( -алгебра), порожденная опреде-

ленным выше классом B, совпадает с булевой алгеброй ( -

алгеброй), порожденной A1 A2.

Упражнение 3.

Вычислить инфинитезимальный оператор винеровского процес-

са.

Упражнение 4.

Для процесса, плотность вероятности которого удовлетворяет следующему уравнению

найти инвариантную меру при условии b a.

Упражнение 5.

Пусть 0,1,2,3,4,5,6 . Описать все борелевские поля (буле-

вы -алгебры, см. определение 3.12), содержащие следующие множества: A1 2,3,4 и A2 4,6 .

Упражнение 6.

Доказать, что каждое конечное борелевское поле A подмножеств порождается некоторым конечным разбиением . Дру-

437