
Климанов Дозиметрическое планирование лучевой ч2 2008
.pdf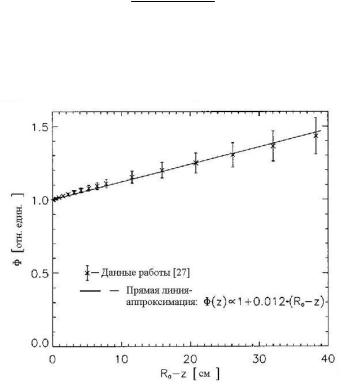
E(z) = |
1 |
(R0 − z)1/ p . |
(2.28) |
|
α1/ p |
||||
|
|
|
Линейная тормозная |
способность с учетом (2.28) теперь |
|||||
определяется из формулы |
dE |
|
1 |
|
|
|
S(z) = − |
= |
(R0 − z)(1/ p)−1 . |
(2.29) |
|||
dz |
pα1/ p |
|||||
|
|
|
|
|||
При энергии протонов выше ~ 20 МэВ имеется ненулевая вероятность выбывания протона из пучка вследствие неупругого ядерного взаимодействия. Вероятность такого события на остаточном
пробеге R0 − z , табулированную в работе [27], можно считать согласно работе [28] пропорциональной
Φ(z) |
1 |
|
1− p(R0 − z) . |
(2.30) |
Таким образом, уменьшение флюенса на интервале z = 0 ÷ R0
приближенно аппроксимируется прямой линией [28]: |
|
Φ(z) 1+β(R0 − z), |
(2.31) |
которая вместе с данными работы [27] показана на рис. 2.14.
Рис. 2.14. Ослабление флюенса протонов в соответствии данными работы [27], используя уравнение (2.30), и аппроксимация ослабления линейной зависимостью [23]
121
Несколько лучшая аппроксимация получается при использовании степенного закона в виде:
Φ(z) 1 + 0,018(R0 − z)0,87 , |
(2.32) |
однако далее для простоты используется линейная аппроксимация со значением β = 0,012 см-1 и нормализованная на величину первичного флюенса:
Φ(z) = Φ0 |
1+β(R0 − z) |
. |
(2.33) |
||||||
|
1 |
+βR0 |
|||||||
|
|
|
|
|
|||||
Из (2.33) следует, что изменение флюенса на глубине z равно |
|
||||||||
− |
dΦ |
|
= Φ |
|
β |
. |
(2.34) |
||
dz |
|
|
|||||||
|
|
|
0 1+βR0 |
|
|
|
|||
Теперь глубинное дозовое распределение без учета флуктуаций в потерях энергии можно найти, подставляя (2.28), (2.29), (2.33) и (2.34) в уравнение (2.25). В результате получаем
)
D(
|
|
|
(R0 − z)(1/ p)−1 + (β + γβp)(R0 − z)1/ p |
для z < R0 |
|
||
z) = |
Φ0 |
|
|
|
. |
||
ρpα1/ p (1+βR |
0 |
) |
|||||
|
|
|
|
|
|
|
|
|
|
для z > R0 |
|
|
|
|
|
|
0 |
|
|
|
|
||
(2.35)
Выражение (2.35) удобно разделить на два слагаемых:
D(z) = D1 (z) + D2 (z) = a1 (R0 − z)(1/ p)−1 + a2 (R0 − z)1/ p . (2.36)
Первый член в (2.36) является вкладом в дозу от протонов, не испытавших ядерных взаимодействий. Он пропорционален тормозной способности (без ядерных взаимодействий) и в некоторой степени повторяет форму кривой Брэгга: монотонно растет в интервале от 0 до R0 и имеет пик при R0. Однако из-за неучета флуктуаций он имеет
особенность при z = R0. Второй член D2 (z) представляет собой дозу,
создаваемую относительно небольшой фракцией протонов, которые испытывают ядерные взаимодействия. Он уменьшается монотонно с
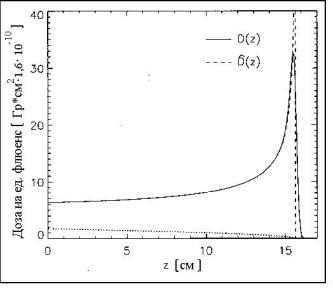
ростом z до нуля при z = R0 (рис. 2.15). Отметим, что D2 (z) включает
дозу, создаваемую не только ядерными взаимодействиями, но также и неядерными взаимодействиями, которые имеют место перед ядерным взаимодействием. Формула (2.35) дает значение дозы в МэВ/г, если ρ выражено в г/см3.
122
)
Рис. 2.15. Кривые Брэгга с учетом D(z) и без учета D(z) флуктуаций для 150 МэВ протонов в
воде. Точечные линии внизу графика – дозовый вклад от протонов, испытавших ядерные взаимодействия [23]
7.2. Дозовое распределение с учетом флуктуаций
Рассмотрим сначала только протоны, которые не испытали ядерных взаимодействий, т.е. член D1 (z) . Вследствие статистической природы
взаимодействия можно предположить, что распределение пробегов протонов, которые потеряли всю свою энергию E0, является гауссовским [29]. Аналогично, распределение глубины, на которой протоны теряют часть их энергии ∆E = E0 _ E , тоже описывается
гауссовским распределением около средней глубины z(E, E0 ) со стандартным отклонением σ(z). Таким образом, имеется
неопределенность в глубине, на которой протоны имеют остаточную энергию E, что можно рассматривать как флуктуацию глубины. С другой стороны, остаточная энергия E точно определяет тормозную
способность, а, следовательно, иD1 . Поэтому доза, создаваемая после того, как протоны потеряют энергию ∆E = E0 _ E , может быть записана в виде D1 (z(E, E0 )). Отсюда доза D1 (z) на конкретной глубине z получается через свертку:
123

|
) |
R |
) |
(z) e |
−( z−z )2 / 2σ2z ( z ) |
|
D1 (z) = |
D1 |
(z) = ∫0 0 |
D1 |
dz . |
(2.37) |
|
|
|
|
|
|
2πσz (z) |
|
Расчет D2(z) с учетом флуктуаций представляет более сложную проблему. Однако необходимость в ее строгом решении является менее актуальной, так как вклад в дозу этих протонов существенно меньше и представляет гладкую функцию глубины. Поэтому учет флуктуаций
для D2(z) допустимо провести таким же способом, как и для D1(z) , т.е.
заменить в уравнении (2.37) D1 на D2 .
Дисперсия σz (z) в уравнении (2.37) меняется от нуля при z = 0 до
максимального значения σ при z = R0. Тем не менее при интегрировании (2.37) можно без заметной погрешности считать ее
постоянной и равной σz (z) ≡ σ, |
так |
как |
в той области, где |
σz (z) существенно меньше, чем |
σ, D1 |
и |
D2 являются гладкими |
функциями. В результате после подстановки в (2.37) D(z) = D1(z)+D2(z) и интегрирования получается [23] следующая формула:
D(z) = Φ0 |
e−ς2 / 4 |
σ1/ p Γ(1/ p) |
× |
|
|||
2πρpα1/ p (1+βR0 ) |
|
||||||
|
|
|
|
(2.38) |
|||
|
1 |
|
|
β + γβ)Υ−1/ p−1 |
|
||
Υ−1/ p (−ς) + ( |
, |
||||||
× |
(−ς) |
||||||
|
σ |
|
|
p |
|
|
|
где ς = (R0 − z) / σ; Γ(x) – гамма функция; |
Υy (x) – параболлическая |
||||||
цилиндрическая функция [30].
Величина σ = σmono для первоначально моноэнергетического пучка
зависит от R0 (или E0) и аппроксимируется в работе [23] следующим уравнением:
σ2 ≈ α′ |
p3α2 / p |
R03−2 / p , |
(2.39) |
|
3p − 2 |
||||
|
|
|
где α′имеет тот же смысл, что и α. Для воды в работе [23] получено, что α′ = 0,087 МэВ2/см и, соответственно,
σ ≈ 0,012R00,935 , (2.40)
где R0 и σ выражены в сантиметрах [31]. Это означает, что σ приблизительно пропорциональна R0 и составляет около 1 % от R0.
124
Пример расчета по формуле (2.38) дозового распределения в воде для 150 МэВ протонов приводится на рис. 2.15.
7.3. Учет энергетического спектра пучка
Реальные клинические пучки протонов не являются моноэнергетическими и определяются особенностями конкретного ускорителя. Безусловно, имеется возможность представить дозовое распределение для конкретного спектра в виде суперпозиции распределений для моноэнергетических источников. Однако в этом варианте нельзя получить аналитическое решение для общего случая, поэтому в работе [23] были приняты упрощающие допущения.
Типичный энергетический спектр состоит из двух частей: (а) пик, который возможно аппроксимировать гауссовским распределением
около E = E0 ; (б) относительно небольшой “хвост”, простирающийся к низким энергиям. Так как дисперсия распределения Гаусса в общем случае невелика ( σE ,0 <<E), то соотношение пробег-энергия (2.26)
можно линеаризировать вокруг E = E0 . Тогда распределение Гаусса
по энергии трансформируется в распределение Гаусса по пробегам с дисперсией:
|
2 |
2 |
2 |
|
|
2 |
2 |
|
2 |
|
2 |
2 p−2 |
|
|
|
dR0 |
|
2 |
|
|
|
||||||||
σ |
|
= σmono + σE,0 |
|
|
|
= σmono + σE ,0 |
α |
|
p |
|
E0 |
. (2.41) |
||
|
|
|
|
|||||||||||
|
|
|
|
dE0 |
|
|
|
|
|
|
|
|
|
|
Следовательно, если энергетический спектр имеет Гауссовское распределение, то это можно учесть простым увеличением σ в уравнении (2.38).
Рассмотрение хвоста энергетического спектра является более сложной задачей, так как его форма зависит от многих факторов. Однако и здесь допустимы существенные упрощения, если принять во внимание, что вклад в дозу от хвоста протонов невелик. Автор [23]
принял, что ΦE(E) E |
|
для 0 ≤ E ≤ E0 . |
Нормализация интеграла от |
|||
ΦE(E) к εΦ0 дает: |
|
|
|
|
|
|
Φ |
E |
(E) = εΦ |
0 |
2E |
. |
(2.42) |
|
||||||
|
|
E02 |
|
|||
Для вычисления глубинного дозового распределения следует преобразовать спектр протонов по энергии ΦE(E) в спектр по длинам
125

пробега ΦR (R) , |
используя ΦR (R) = ΦE (E(R))dE / dR . |
Учитывая |
|||||||||
(2.26), а также, что (2/p __1)<<1, т.е. p ≈ 2 , получаем: |
|
||||||||||
Φ |
R |
(R) = εΦ |
|
2R2 / p−1 |
≈ εΦ |
0 |
1 |
= const. |
(2.43) |
||
0 E02 pα2 / p |
R0 |
||||||||||
|
|
|
|
|
|
||||||
Теперь спектр по пробегам хвоста (англ. tail) протонов необходимо свернуть с глубинным дозовым распределением для моноэнергетических протонов. Проводя эту операцию для Dtail, ввиду малости ε пренебрежем ядерными взаимодействиями протонов, считая,
что D(z) = D1 (z). В результате приходим к выражению |
|
× |
||||||||||
D (z) ≈ |
1 |
|
0 |
Φ (R)D (z, R)dR ≈ |
|
εΦ0 |
|
|
||||
) |
|
|
|
R |
|
) |
|
|
|
|
|
|
tail |
|
|
|
∫z |
R |
|
1 |
|
|
|
|
|
|
Φ0 |
|
R0ρpα1/ p (1+βR0 ) |
|
||||||||
|
|
|
|
|
|
|||||||
R0 |
|
|
1/ p−1 |
|
|
εΦ0 |
|
|
1/ p |
|
|
|
×∫z |
(R − z) |
|
|
dR = |
|
|
(R0 − z) |
|
. |
(2.44) |
||
|
|
R |
ρpα1/ p (1+βR ) |
|
||||||||
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
Заметим, что формула (2.44) имеет вид аналогичный виду второго члена в уравнении (2.35). Это дает основание учесть флуктуации для
Dtail так же, как это сделано в разделе 7.2. Добавление результата в уравнение (2.38) дает следующую формулу:
D(z) = Φ |
0 |
|
e−ς2 / 4σ1/ p Γ(1/ p) |
[ |
1 |
Υ |
−1/ p |
(−ς) + |
||
|
2πρpα1/ p |
|
σ |
|||||||
|
|
(1+βR0 ) |
|
(2.45) |
||||||
|
β |
|
ε |
|
|
|
|
|
||
|
|
|
|
|
|
|||||
|
|
+ γβ+ |
|
|
(−ς)] |
|
|
|||
+ |
p |
R0 |
Υ−1/ p−1 |
|
|
|||||
|
|
|
|
|
|
|
|
|||
С первого взгляда формула (2.45) выглядит достаточно громоздкой. Константы, входящие в ее состав, приводятся в табл. 2.3. Однако для ζ
> 10 (т.е. z < R0 −10σ) D(z) совпадает с D(z) с погрешностью 0,5 %
(см рис. 2.15). В то же время для ζ < -5 (т.е. z > R0 +5σ) D(z) пренебрежимо мала. Поэтому можно D(z) аппроксимировать
следующим выражением: |
|
|
|
) |
для z < R0 −5σ |
|
|
D(z) |
|
|
|
|
для R0 −10σ ≤ z ≤ R0 |
|
(2.46) |
D(z) = D(z) |
+ 5σ . |
||
|
|
|
|
0 в остальных случаях |
|
|
|
126
Таблица 2.3
Значения констант и параметров, используемые в теоретической модели (2.45). Все значения приводятся для протонов в воде. Последние два параметра зависят
от ускорителя и линии пучка. Величина σ рассчитывается из σmono и σE,0 по формуле (2.41)
Константа |
Описание |
Значение |
Единица |
|
|
|
измерения |
p |
Показатель в соотношении энергия-пробег |
1,77 |
1 |
α |
Коэффициент пропорциональности |
0,0022 |
см·МэВp |
R0 |
Пробег |
p |
см |
|
|
αE0 |
|
β |
Параметр наклона уменьшения флюенса |
0,012 |
см-1 |
|
Доля локальной поглощенной энергии, |
|
1 |
γ |
освобожденной при неупругих ядерных |
0,6 |
|
|
взаимодействиях |
|
|
σmono |
Ширина распределения пробегов, обусловленная |
0,12R00,935 |
см |
|
флуктуациями |
|
|
σE,0 |
Ширина распределения протонов по энергии |
≈0,01E0 |
МэВ |
ε |
Первичного флюенса, переходящего в хвост |
≈ 0 – 0,2 |
1 |
|
энергетического спектра |
|
|
Для распространения протонов в воде окончательные формулы, полученные с использованием табл. 2.3, и учитывая, что для воды Γ(1/ p) = 1,575, имеют следующий вид:
) |
|
Φ0 |
|
|
|
− z)−0,435 + |
|
|
|
|
|
Dw (z) = |
[17,93(R0 |
|
|
|
|
||||||
1+ 0,012R0 |
|
|
|
(2.47) |
|||||||
|
|
|
|
|
|
|
|
|
|
||
и |
+ (0,444 + 31,7ε/ R0 (R0 |
− z)0,565 |
|
|
|
|
|||||
e−(R0 −z)2 / 4σ2 σ0,565 |
|
|
|
|
|
|
|||||
|
|
|
R |
|
− z |
|
|||||
Dw (z) = Φ0 |
|
|
|
×[11,26σ−1Υ−0,565 (− |
|
0 |
|
) + |
|||
1 |
+ 0,012R0 |
|
|
|
σ |
||||||
|
|
|
R0 − z |
|
|
|
(2.48) |
||||
+ (0,157 +11,26ε/ R0 )Υ−1,565 (− |
)]. |
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
σ |
|
|
|
|
|
Корректность разработанного метода была опробована автором [23] путем сравнения с экспериментальными данными и численными расчетами. Так как спектр пучков протонов, вообще говоря, точно не известен, то параметры σ, ε и R0 варьировались для получения
127
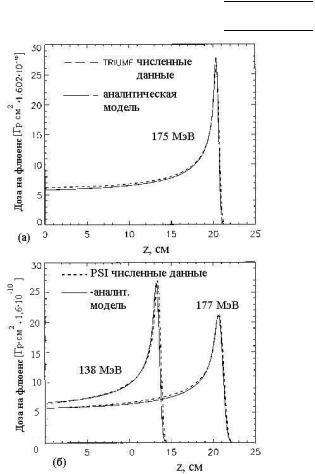
наилучшего согласия. Обычно оказывалось достаточно нескольких итераций. Сравнение результатов расчетов по данной методике с экспериментом и численными данными иллюстрируется в табл. 2.4 и на рис. 2.16.
Таблица 2.4
Параметры для уравнения (2.48), дающие наилучшее совпадение с опубликованными экспериментальными данными [20,32], и максимальные расхождения между экспериментом и расчетом
Источник |
R0, cм |
σ, см |
ε, % |
Максимальные отклонения |
|
|
|
|
|
% |
см |
Б. Ларрсон [32] |
23,4 |
0,29 |
2 |
-2,3 |
+0,14 |
А. Коелер и др. [20] |
15,8 |
0,27 |
5 |
-2,5 |
-0,10 |
Рис. 2.16. Сравнение результатов расчета по аналитической модели с численными данными, полученными по численным алгоритмам TRIUMF [33] и PSI [34]
128
Расхождение с экспериментальными данными, представленные в табл. 2.4, даются в процентах для района плато и в сантиметрах для пика Брэгга. Автор аналитической модели [23] провел сравнение своих результатов также с экспериментальными данными HCI и работы [33]. Совпадение между результатами оказалось еще лучше, чем показано в табл. 2.4. Аналогичные результаты получены и при сравнении аналитической модели с данными численных расчетов (рис. 2.16).
8. Метод тонкого луча
Метод тонкого луча в своей классической постановке (см. Часть 1 настоящего пособия) оказался весьма подходящим для дозиметрических расчетов и в протонной терапии. В настоящее время во многих центрах используются системы планирования, основанные на использовании этого алгоритма. Одной из первых публикаций, посвященных применению метода тонкого луча (ТЛ) для расчета дозовых распределений от протонов, была работа П. Петти [35]. Однако в этой работе не учитывалась модификация пучка протонов в материалах и устройствах, находящихся в пучке до падения протонов
на облучаемый объект. В более поздней работе Л. Хонг с коллегами
[36] усовершенствовали алгоритм ТЛ для учета устройств, расположенных на линии пучка и модифицирующих пучок (см. рис. 2.10) после его расширения в системе фольг. Рассмотрим метод ТЛ
вварианте, разработанном в этой работе [36], начав с линии пучка.
8.1.Расчет модифицирующих устройств линии пучка
8.1.1. Геометрия линии пучка и входные данные
Геометрия линии пучка, принятая в работе [36] (рис. 2.17) достаточно традиционна и моделирует систему Циклотронной Лаборатории Гарварда. Устройства, модифицирующие пучок, делятся на два вида: устройства, ограничивающие поперечные размеры пучка и устройства не ограничивающие пучок. К первым относятся коллиматоры, апертуры (диафрагмы), блоки. Они считаются “идеальными”, т.е. они не влияют на открытую часть пучка и полностью поглощают частицы, падающие на них. Вторые поглощают
129

часть энергии и рассеивают протоны. Рассеяние увеличивает поперечные размеры и полутень пучка (англ. penumbra) и может влиять на дозовое распределение внутри пациента и на конце пробега.
Рис.2.17. Геометрия линии пучка, принятая в работе [36]
Термин “открытый пучок” относится к пучку протонов, свободному от всех модифицирующих устройств за исключением тех, которые постоянно находятся в пучке. Это включает систему расширения пучка, мониторные ионизационные камеры и систему крепления коллиматоров. Открытый пучок не включает также модулятор пробегов и, следовательно, имеет так называемый “чистый”(близкий к моноэнергетическому) пик Брэгга, а не ППД.
В алгоритме работы [36] открытый пучок моделируется виртуальным эффективным источником с конечным поперечным сечением, локализованным в некоторой эффективной точке пространства. Расстояние от эффективного источника до изоцентра принимается как расстоянием источник-ось (РИО). Размеры эффективного источника параметризуются двумерным распределением Гаусса, стандартное отклонение которого является эффективным радиусом источника. РИО определяется из экспериментальных измерений распределения дозы в воздухе, предполагая, что оно подчиняется закону обратных квадратов. Эффективный размер источника определяется с помощью измерения полутени открытого пучка в воздухе с блоком, размещенным на оси пучка. Алгоритм требует также знания из эксперимента или расчета (см. предыдущий
130
