11.2.Упругость

11.2.1.Закон Гука для случая одноосной деформации

Начальный участок кривой растяжения, характеризующийся прямой пропорциональностью между нагрузкой и удлинением, соответствует области упругого поведения материала. Закономерности упругого поведения металлов были впервые установлены Робертом Гуком. В простейшем виде, применительно к случаю растяжения образца до степени деформации, не превышающей 1%, закон Гука выглядит следующим образом:

Поскольку закон Гука справедлив лишь при малых деформациях, когда σ = S и ε = e, допустимы обе его записи, приведенные выше.

Коэффициент пропорциональности Е, связывающий напряжение и деформацию, называется модулем упругости при одноосном растяжении, или модулем нормальной упругости, или модулем Юнга и является константой материала, характеризующей его жесткость. При одноосном растяжении величина Е характеризует интенсивность увеличения нагрузки с ростом удлинения, т.е. определяет наклон начального участка диаграммы растяжения. Модуль нормальной упругости не зависит от знака деформации,

– его величины при растяжении и при сжатии одинаковы.

11.2.2. Закон Гука как результат взаимодействия соседних атомов

Закон Гука может быть выведен из рассмотрения энергии упругого взаимодействия атомов в кристаллической решетке металлического материала. Между двумя соседними атомами в решетке металлического образца, не подвергнутого действию внешних сил и свободного от внутренних напряжений (рис. 11.7), действуют взаимно уравновешенные силы притяжения и отталкивания. На

29

ду двумя атомами описывается аналогичными кривыми (рис. 11.8). На бесконечно большом расстоянии энергия связи равна нулю. При сближении атомов совершается работа, величину которой вычитаем из исходной нулевой энергии. В результате получаем кривые энергии притяжения 1, энергии отталкивания 2 и результирующую энергетическую кривую 3, минимум которой соответствует положению равновесия а0.

Если к телу приложена сила, вызывающая упругую деформацию, то расстояние между атомами изменяется и устанавливается новое положение равновесия, в котором изменившиеся силы межатомного взаимодействия компенсируют приложенную внешнюю силу. Смещение атомов из исходного положения равновесия характеризуется разностью между но-

вым и старым значениями межатомного расстояния:

где а – новое расстояние между атомами. Если приложенная сила f – растягивающая, то a > a0 и u положительно. При сжатии a < a0 и u < 0. Условие равновесия можно записать как

30

где Φ(u) – энергия связи при смещении u. Если под действием приложенной силы f происходит малое смещение du, то при этом совершается работа fdu. Эта работа компенсируется изменением энергии связи dΦ(u) = Φ(u + du) – Φ(u). При снятии внешней нагрузки атомы возвращаются в исходные положения на расстоянии a0 друг от друга, а образец приобретает первоначальные размеры, которые он имел до нагружения.

Закон Гука может быть выведен при соблюдении трех условий:

1)непрерывность функции Φ(u);

2)минимум dΦ/du = 0 при u = 0;

3)смещение u << a0 .

Первое условие позволяет разложить функцию энергии взаимодействия в ряд Тейлора:

Φ(u) = Φ0 + u (dΦ/du)0 + 12 u2 (d 2Φ/du2)0 + члены,

В этом уравнении Φ0 – энергия взаимодействия при u = 0 и все производные взяты в точке u = 0. Поскольку dΦ/du равно нулю при u = 0, а членами, содержащими u в третьей и более высоких степенях, можно пренебречь в силу малости u, получаем

Вторая производная (d2Φ/du2)0 – это кривизна функции Φ(u) в точке u = 0; следовательно, она не зависит от u и является константой. Таким образом, получаем:

т.е. закон Гука: сила пропорциональна смещению.

При достаточном увеличении смещения u уже нельзя пренебрегать членами, содержащими u в более высоких степенях, так что зависимость f(u) должна отклониться от линейной. На практике с этим явлением не приходится сталкиваться, потому что при еще более низких напряжениях в металлах начинается необратимая пластическая деформация. Закон прямой пропорциональности при

31

этом нарушается, но совсем по иным причинам, связанным с наличием в металле дислокаций. Исключение составляют совершенные нитевидные бездислокационные металлические кристаллы, в которых пластическое течение затруднено и в которых при упругой деформации на несколько процентов наблюдается отклонение от закона Гука.

По аналогии с выражением для закона Гука σ = Еε, устанавливающим связь между растягивающим (или сжимающим) напряжением и деформацией в том же направлении, может написано выражение, устанавливающее связь между касательным напряжением t и вызываемым им сдвигом γ:

где G – модуль сдвига (или модуль упругости при сдвиге).

При гидростатическом сжатии (или растяжении) закон Гука выражает прямую пропорциональность между гидростатическим дав-

11.2.3. Закон Гука в обобщенном виде

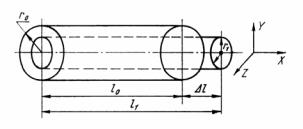
При одноосном растяжении стержня происходит не только увеличение его длины, т.е. изменение размера вдоль оси х, но и уменьшение диаметра, т.е. сжатие вдоль двух других осей y и z (рис. 11.9). Таким образом, одноосное напряженное состояние приводит к возникновению трехосной деформации.

Рис. 11.9. Изменение размеров при одноосном растяжении стержня

Отношение ν изменения размеров в поперечном направлении к их изменению в продольном направлении называется коэффициентом Пуассона:

32

Закон Гука в своей обобщенной форме устанавливает линейную зависимость между напряжениями и деформациями в любых направлениях, т.е. между каждым компонентом тензора напряжений и каждым компонентом тензора деформаций:

γxy = txy /G ; γxz = txz /G ; γyz = tyz /G .

Между четырьмя константами упругости изотропного тела сущест-

которые позволяют определить все константы, если известны любые две из них.

Приведенная выше форма записи закона Гука справедлива лишь для изотропных тел, в которых любые произвольно выбранные направления эквивалентны. Достаточно массивный металлический поликристалл, состоящий из множества хаотически ориентированных кристаллитов, каждый из которых обладает определенной анизотропией свойств, можно считать квазиизотропным. При нагружении взятого отдельно кристаллита (монокристалла) уже недостаточно знания двух констант упругости, чтобы установить связь между напряженным и деформированным состояниями. Картина значительно усложняется вследствие анизотропии монокристалла.

В общем случае анизотропного тела закон Гука устанавливает прямую пропорциональность между каждым компонентом тензора деформаций и всеми шестью компонентами тензора напряжений:

Sx = c11ex + c12ey + c13ez + c14γxy + c15γyz + c16γxz;

Sy = c21ex + c22ey + c23ez + c24γxy + c25γyz + c26γxz ;

Sz = c31ex + c32ey + c33ez + c34γxy + c35γyz + c36γxz ;

txy = c41ex + c42ey + c43ez + c44γxy + c45γyz + c46γxz; (11.21)

tyz = c51ex + c52ey + c53ez + c54γxy + c55γyz + c56γxz; tzx = c61ex + c62ey + c63ez + c64γxy + c65γyz + c66γxz.

33