
Елтаренко Исследование операцыи 2007
.pdf
|
|
|
|
S0 |
S1 |
S2 |
|
Sn |
|
|
|
|
S0 |
q0 |
q1 |
q2 |
|
qn |
|
|
|
|
S1 |
q0 |
q1 |
q2 |
|
qn |
|
|
Pmn |
|
S2 |
0 |
q0 |
q1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
... ... ... |
qn m 1 |
... |
||
|
|
|
Sm ... ... ... ... |
... |
|||||
|
|
|
|
|
|||||
|
|
|
|
... ... ... ... |
|
|
... |
||
Отметим, что |
qn 1. |
|
|
|
|
|
|
||
|
n 0 |
|
|
|
|
|
|
|
|
Строка S0 матрицы совпадает со строкой |
S1 , потому что рас- |
||||||||
сматривается интервал между моментами регенерации (моментами выхода заявки из СМО). Эти интервалы не отличаются, была ли в СМО одна заявка в предыдущий момент регенерации (она находилась на обслуживании) или заявок в СМО вообще не было.
Составим систему уравнений для нахождения предельных вероятностей.
P |
P q |
Pq |
|
|
|
|||
0 |
0 |
0 |
1 |
0 |
|
|
|
|
P |
P q |
Pq |
|
P q |
|
|||
1 |
0 |
1 |
1 |
1 |
2 |
0 |
|
|
|
|
|
n 1 |
|
|
|
|
|
P |
P q |
|
|
Pq |
1 i |
, (n 0,1, 2,...) |
||
n |
0 |
n |
|
|
i |
n |
|
|
|
|
|
i |
0 |
|
|
|
|
Используем Z–преобразование для определения характеристик СМО (основные положения Z–преобразования приведены в приложении 3):
P(z) |
P zn ; |
|
n |
|
n 0 |
70

|
|
|
|
|
zn P q |
|
zn |
n 1 |
|
|
|
|
|
|
||||||
|
|
P(z) |
|
|
|
Pq |
n 1 i |
. |
|
|
|
(1.43) |
||||||||
|
|
|
|
|
|
|
|
0 |
n |
|
|
|
i |
|
|
|
|
|
||
|
|
|
|
n |
0 |
|
|
|
|
|
n 0 |
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
P0Q( z) |
|
|
|
|
|
|
|
|
|
|
|
||||
Преобразуем второе слагаемое: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
n 1 |
|
|
|
|
|
|
1 |
|
n 1 |
|
|
|
|
|
||
|
|
|
zn |
Pq |
|
|
|
|
zn 1 |
Pq |
|
|
|
. |
|
|||||
|
|
|
n |
1 i |
|
|
n |
1 i |
|
|
||||||||||
|
|
|
|
|
i |
|
|
|
z n |
|
|
i |
|
|
|
|||||
|
|
n 0 |
|
i |
0 |
|
|
|
|
|
|
0 |
i |
0 |
|
|
|
|
|
|
Сделаем замену n |
1 |
k : |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
k |
|
|
|
|
|
|
1 |
|
|
k |
|
|
|
|
|
|
|
|
zk |
Pq |
|
|
|
|
zk |
Pq |
|
P q |
|
. |
|||||||
|
|
|
k |
|
i |
|
|
k |
||||||||||||
|
|
z k 1 |
|
|
i |
|
|
z k 0 |
|
i |
k i |
|
0 |
|
|
|||||
|
|
|
i |
0 |
|
|
|
|
|
i |
0 |
|
|
|
|
|
|
|||
1 |
zk |
k |
|
|
1 P |
|
zk q |
|
1 P(z)Q(z) |
|
1 P Q(z) . (1.44) |
|||||||||
Pq |
|
|
|
|
||||||||||||||||
z k 0 |
|
i 0 |
i |
k i |
z |
0 k 0 |
|
k |
z |
|
|
|
z |
0 |
|
|||||
Выражение (1.44) можно также получить, используя свойство Z– |
||||||||||||||||||||
преобразования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
z |
n |
P |
|
1 (P(z) P ) . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
n 1 |
|
z |
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя (1.44) в (1.43), получим:
P(z) P Q(z) |
|
1 P(z)Q(z) |
1 P Q(z) . |
|
||||||||||||||
0 |
|
|
|
|
|
z |
|
|
|
|
|
z |
0 |
|
|
|||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P Q(z)(1 |
|
1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
P0Q(z)(z |
1) |
|
|
|
||||||||||||
0 |
|
|
|
|
z |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(1.45) |
|
1 |
|
|
|
|
|
|
|
|
z |
|
Q(z) |
|
|
||||
1 |
Q(z) |
|
|
|
|
|
|
|
||||||||||
z |
|
|
|
|
|
|
|
|
|
|
||||||||
Рассмотрим подробнее Q z : |
|
|
|
|
|
|
|
|
|
|
||||||||
Q(z) |
z |
k |
q |
|
|
|
|
z |
k ( |
t)k |
e |
t |
(t)dt ; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
k 0 |
|
|
|
|
|
k 0 |
|
|
0 |
|
|
|
|
|
|
||
|
Q(z) |
|
|
|
( |
tz)k |
e t |
(t)dt ; |
|
|||||||||
|
|
|
|
|
|
|
|
k! |
|
|||||||||
|
|
|
|
0 |
k 0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
71 |
|
|
|
|
|
|
|
|
|
|
|||

|
Q(z) |
e t ( z 1) (t)dt ; |
|
||||
|
|
0 |
|
|
|
|
|
|
Q (z) |
te t ( z 1) (t)dt ; |
|
||||
|
z |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Qz (1) |
t (t)dt |
M (t) ; |
(1.46) |
|||
|
0 |
|
|
|
|
|
|
|
Q (z) |
2t 2e t ( z 1) (t)dt ; |
|
||||
|
z |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Q (1) |
2 M(t 2 ) |
2 |
D(t) |
M 2 (t) . |
(1.47) |
||
z |
|
|
|
|
|
|
|
Чтобы определить |
P0 в (1.45), |
надо использовать свойство Z– |
|||||
преобразования: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
P z |
|
z |
1 1. |
|
|
|
|
|
|
|
||||
При подстановке в (1.45) z 1 получим неопределенность. При-
меним правило Лапиталя для нахождения предела lim P(z).
z 1
Берем производную числителя и знаменателя:
lim P(z) |
lim |
P0Qz (z |
1) |
|
P0Q(z) |
|
P0Q(1) |
1. |
||
1 |
Qz (z) |
1 Qz (1) |
||||||||
z 1 |
z 1 |
|
||||||||
|
|
|
|
|
|
|
|
|||
Учитывая (4) и тот факт, что Q(1) |
|
1, получим: |
|
|||||||
|
|
|
|
P0 |
|
1. |
|
|
|
|
|
|
1 |
M(t) |
|
|
|
||||
|
|
|
|
|
|
|||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
P0 1 |
M(t) . |
|
|
(1.48) |
||||
Для существования установившегося режима в СМО (чтобы очередь не росла до бесконечности) необходимо, чтобы M t 1.
Получим выражение для определения Ls . Для этого возьмем производную от P z :
72

Ls Pz (z) P0 |
Qz (z |
1) Q(z) z |
Q(z) (1 Q (z))Q(z)(z 1)) |
. |
|||
|
|
|
z Q(z) 2 |
|
|
||
|
|
|
|
|
|
|
|
После преобразования получим: |
|
|
|
|
|||
Pz (z) |
P0 |
z(z 1)Qz |
Q(z)(Q(z) 1) |
. |
|
|
|
(z |
Q(z))2 |
|
|
||||
|
|
|
|
|
|
||
Среднее число заявок в СМО равно:
Ls |
Pz (1) P0 lim |
z(z 1)Qz |
Q(z)(Q(z) 1) |
. |
|
(z |
Q(z)) |
2 |
|||
|
z 1 |
|
|
||
|
|
|
|
|
|
Чтобы разрешить неопределенность, воспользуемся правилом Лапиталя:
|
|
|
Q (z2 |
z) 2zQ 2Q Q(z) |
|
|
L |
P lim |
|
z |
z |
; |
|
|
|
|
||||
s |
0 |
z 1 |
|
2(z Q(z))(1 Qz ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P0 |
|
L |
lim[Q |
Q (z)(z2 |
z) |
] . |
|
|
|
||||
s |
z 1 |
z |
2(z Q(z)) |
|
|
|
|
|
|||
|
|
|
|
|
|
Чтобы вновь снять неопределенность, еще раз воспользуемся правилом Лапиталя:
|
|
|
Q (3) (z2 |
z) |
|
|
Q (2z |
1) |
|
|||
Ls lim Qz |
lim |
|
z |
|
|
|
z |
|
; |
|||
|
|
|
2(1 |
Qz ) |
|
|||||||
z 1 |
z |
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
Ls |
Qz |
(1) |
|
|
Qz |
(1) |
|
|
. |
|
|
(1.49) |
|
|
2(1 Qz (1)) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
После подстановки в (1.49) выражения (1.46) и (1.47), получим: |
||||||||||||
Ls |
M(t) |
|
|
2(D(t) M 2(t)) |
, |
|
(1.50) |
|||||
|
|
|
|
|||||||||
|
|
|
2(1 |
M(t)) |
|
|
||||||
которая носит имя формулы Хинчина –Поллачека.
эфф |
; Ws |
Ls ; |
Wq |
Ws M t ; |
|||
|
|
2 |
[D(t) M 2 (t)] |
|
|||
L |
W |
L |
|
|
|
|
. |
|
|
|
|
||||
q |
q |
q |
2(1 |
M(t)) |
|
||
|
|
|
|
|
|||
|
|
73 |
|
|
|
|
|

Примеры анализа СМО методом вложенных цепей Маркова Пример 1. Пусть t

 M t
M t 1 и D t
1 и D t 1 2 .
1 2 .
При подстановке математического ожидания и дисперсии в формулу Хинчина–Поллачека получаем ту же формулу Ls , которая была получена в п. 1.4.1 для пуассоновских систем:
|
|
|
2 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
Ls |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
2(1 |
) |
|
|
|
1 |
1 |
|||||||||
|
|
|
|
|
|
|
||||||||||
Пример 2. Пусть T – время обслуживания – постоянная величина, |
||||||||||||||||
т.е. M t T, |
D t |
0. После подстановки в формулу Хинчина– |
||||||||||||||
Поллачека получим выражение для Ls : |
|
|
|
|
|
|
||||||||||
|
|
|
|
Ls |
|
T |
|
|
|
2T 2 |
. |
|
|
|
||
|
|
|
|
|
|
2(1 |
T) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
СМО с произвольным входным потоком |
|
|
|
|
||||||||||||
Класс СМО |
f t , |
e t , m |
1, n |
|
|
. |
|
|
|
|
|
|||||
В этом случае моменты регенерации системы – моменты поступ-
ления заявок в СМО. |
|
|
|
|
|
|
|
|||
Матрица переходов из одного состояния в другое |
|
имеет вид: |
||||||||
dkn |
||||||||||
|
|
|
|
S0 |
S1 |
S2 |
S3 |
Sn |
||
|
|
|
S0 |
h0 |
d0 |
0 |
0 |
0 |
||
|
|
|
S1 |
h1 |
d1 |
d0 |
0 |
0 |
||
|
dkn |
|
S2 |
h2 |
d2 |
d1 |
d0 |
0 |
||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn 1 |
hn 1 |
dn 1 |
dn 2 |
dn 3 |
d0 |
||
|
|
|
|
|
|
|
. |
. |
||
74

где d0 – вероятность того, что между моментами регенерации СМО будет обслужено 0 заявок; dn – вероятность того, что между момен-
тами регенерации СМО будет обслужено ровно n заявок, которая определяется по формуле:
|
d |
|
|
( t)n |
e |
|
n f (t)dt . |
||||||||||
|
n |
|
|
n! |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятности hk |
вычисляются из условия, что сумма вероятностей |
||||||||||||||||
по каждой строке равна единице: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
hk 1 |
|
|
|
|
dn . |
|||||||||
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Предельные вероятности найдем из уравнения P P |
dkn |
: |
|||||||||||||||
|
|
|
P |
|
|
|
P d |
k |
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
k |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P2 |
|
|
|
Pk 1dk |
||||||||||
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn |
|
|
|
Pk n 1dk |
||||||||||
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
Будем находить решение системы уравнений в виде: |
|||||||||||||||||
P Bxn , где 0 |
x |
1, а B – постоянный коэффициент. |
|||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bxn |
|
Bxk n 1dk ( n 1, 2, ) |
||||||||||||||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
xk d |
k |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
75

При x (0;1) |
это уравнение имеет единственное решение x0 , по- |
|||||||||||
кажем это (рис. 1.29). Введем обозначение D(x) |
|
|
xk d |
k |
: |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
D 0 d |
0 |
0 ; |
D |
kxk 1d |
k |
0 ; |
|
|
|||
|
|
|
|
x |
|
|
|
|
|
|
||
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
D |
|
k(k 1)xk 2 d |
k |
0 . |
|
|
|
||||
D(x) |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) x |
|
|
|
|
|
||
|
|
|
|
|
|
|
D(x) |
|
|
|
||
d0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x0 |
|
|
|
|
|
|
|
|
1 |
|
x |
|
Рис. 1.29. График функции D x |
|
|
|
|
|||||||
Так как Dx |
0 и |
Dx |
0 , то функция D x |
– выпуклая и моно- |
||||||||
тонно – возрастающая. Чтобы x0 |
было единственным решением, не- |
|||||||||||
обходимо, чтобы D (1) |
1. |
|
|
|
|
|
|
|
|
|
||
D(x) xk dk
k 0
|
|
xk ( t)k |
e |
t |
f (t)dt; |
0 |
k 0 |
k! |
|
||
|
|
|
|||
|
|
||||
e t ( x 1)
D(x) e t(x 1) f (t)dt ;
0
Dx (1) t f (t)dt  M(t) .
M(t) .
0
76

Значит, x0 существует, если |
M t |
|
1. |
|
|
|
|
|
|
|
|
|
|||||||||||
Решая уравнение x |
D x , находим |
x0 . Для определения коэф- |
|||||||||||||||||||||
фициента В воспользуемся соотношением |
|
|
|
Pn |
|
|
1: |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
x n |
|
1; |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
B |
|
1 |
|
1; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
B 1 x0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким образом, P |
1 |
x xn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим характеристики СМО: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Ls |
|
|
|
|
nPn |
; |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
n(1 x )x n |
|
(1 x )x |
|
|
|
nx n 1 |
; |
|
||||||||||||||
s |
|
0 |
|
0 |
|
|
|
|
|
|
|
0 |
0 |
|
|
|
0 |
|
|
||||
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
||
F (x ) |
( |
|
x n ) |
|
|
|
|
|
|
|
1 |
|
|
|
|
; |
|
|
|||||
|
|
|
|
|
|
|
|
x )2 |
|
|
|
||||||||||||
|
0 |
|
|
|
0 |
x0 |
|
|
|
(1 |
|
|
|
|
|
||||||||
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
Ls |
|
|
|
x0 |
|
; |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
x0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Ws |
|
|
Ls M(t) ; |
|
|
|
|
|
|
|
|
|
||||||||
|
|
Wq |
|
Ws |
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
||||||
|
Lq |
|
Wq |
|
|
|
Ls |
|
|
|
1 |
|
|
. |
|
|
|
|
|
||||
|
|
M(t) |
|
|
|
|
|
M(t) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Примеры анализа СМО методом вложенных цепей Маркова |
|||||||||||||||||||||||
Пример 1.Пусть входной поток – пуассоновский, т.е. f |
t |
e t . |
|||||||||||||||||||||
Составим уравнение для определения x0 : |
D x |
|
x ; |
|
|
||||||||||||||||||
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

D x |
x |
k |
d |
|
|
x |
k ( |
t)k e t |
e |
t |
dt ; |
|
|
|
|
|
||||||||
|
|
k |
|
|
k! |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k |
0 |
|
|
|
|
0 k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D(x) |
et( x |
|
) dt |
|
|
|
|
et ( x |
|
) |
|
|
|
|
|
|
|
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x |
|
|
|
|
|
0 |
|
x |
|
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решаем уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x |
x2 |
( |
|
|
|
|
)x |
0. |
|
|
|
|
|||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решением данного уравнения будет |
x0 |
|
|
|
; |
Ls |
|
|
|
, т.е. |
||||||||||||||
|
|
|
1 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получаем ту же формулу Ls , которая была получена в п. 1.4.1 для
пуассоновских систем.
Пример 2. Пусть входной поток в СМО – регулярный, т.е. интер-
вал между поступлениями заявок T const. |
|
|
|
|
|
|
|
|||||||||
Составляем уравнение для x0 : |
D x |
|
x |
|
|
|
|
|
|
|
||||||
|
|
D(x) |
x |
k ( T)k |
e |
T |
|
e |
T (x 1) |
; |
|
|
||||
|
|
|
k! |
|
|
|
|
|
|
|||||||
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e T ( x 1) |
x . |
|
|
|
|
|
|
|
||||
Находим x0 |
из полученного уравнения. |
|
|
|
|
|
|
|
||||||||
Ls |
x0 |
|
; Ws |
LsT ; Wq |
Ws |
|
|
1 |
|
; |
Lq Ls |
1 |
. |
|||
|
|
|
|
|
|
T |
||||||||||
|
1 x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.7. СМО с приоритетами
В данном классе СМО на вход поступают несколько потоков зая-
вок |
разного приоритета. Обозначим эти потоки через |
|
i (i |
1, 2, ...,n) , где i – приоритет. |
Будем считать, что поток 1 |
имеет самый высокий приоритет, а n |
– самый низкий. |
|
78
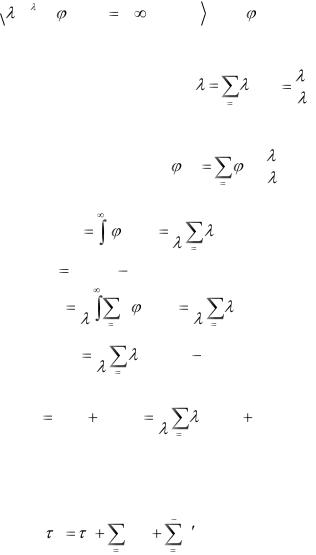
1.7.1. Одноканальные СМО с приоритетами
Класс СМО  ie
ie i t , i (t), m 1, , PRIOR , где i (t) – плотность
i t , i (t), m 1, , PRIOR , где i (t) – плотность
функции распределения времени обслуживания заявок i-го приоритета (произвольный закон).
|
n |
|
|
|
Суммарный поток заявок в СМО равен: |
|
, P |
i |
– веро- |
i |
|
|||
|
i |
|
|
|
|
i 1 |
|
|
|
ятность того, что на входе СМО поступает заявка i-го приоритета. Получим плотность функции распределения времени обслуживания
|
n |
|
|
|
произвольной заявки входного потока: (t) |
|
(t) |
i |
. |
i |
|
|||
|
|
|
|
|
i |
1 |
|
|
|
Математическое ожидание времени обслуживания:
|
|
1 |
n |
Mi (t) t |
i (t)dt |
|
i Mi (t) ; |
|
|||
0 |
|
|
i 1 |
для дисперсии: Di (t) Mi (t2 ) Mi2 (t) ,
M(t |
2 |
) |
1 |
|
|
n |
t |
2 |
|
(t)dt |
|
|
1 n |
|
|
M(t |
2 |
) , |
||
|
|
|
|
|
|
i |
|
|
|
|
|
i |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 i 1 |
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|||
|
D(t) |
1 |
n |
|
[M |
(t |
2 |
) M |
2 |
(t)] . |
|
|
||||||||
|
|
|
|
|
|
i |
|
i |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно также записать:
2 |
2 |
|
1 n |
|
2 |
|
|
M(t |
) D(t) M |
(t) |
|
i |
[D (t) M |
(t)]. |
|
|
|||||||
|
|
|
|
i |
i |
|
|
|
|
|
|
i 1 |
|
|
|
Рассмотрим задачу определения характеристик обслуживания заявок k-го приоритета.
Время ожидания в очереди заявки k-го приоритета будет определяться выражением (рис 1.30):
k |
|
k 1 |
|
k |
niqi |
niqi , |
(1.51) |
ож 0 |
|||
i |
1 |
i 1 |
|
79
