Елтаренко Исследование операцыи 2007

F2

на q2.

Случай 3. Пороговый размер заказа – r r

Целевая функция в этом случае имеет вид (рис.3.10):

Получим уравнение для определения величины r.

После упрощения получим уравнение для определения r:

Многопродуктовая статическая модель с ограничением на емкость склада

Число видов продукции – n, индексы продукции – i=1, 2, .., n. Цены на все виды продукции неизменны. Для каждого вида продукции заданы:

i – спрос в единицу времени,

Ki – затраты на размещение заказа,

hi – затраты на хранение 1 ед. продукции в единицу времени.

141

Кроме этого заданы объемные характеристики одной единицы продукции каждого вида – ai (i = 1, ... ,n), а также общая вместимость склада A (объем в м3 или площадь в м2).

Требуется определить оптимальные размеры заказов по каждому виду продукции yi* .

Целевая функция имеет вид:

Для минимизации целевой функции воспользуемся методом Лагранжа. Составим функцию Лагранжа:

где – множитель Лагранжа (меньше нуля).

Для определения yi* составим систему уравнений:

Из (3.2) получим

При = 0 получаем задачу без ограничения:

Если при этом выполняется ограничение

142

n

i i

i 1

то задача решена.

В случае невыполнения ограничения (3.4) систему уравнений решаем численными методами.

Для этого, на каждом шаге t уменьшая , рассчитываем по формуле (3.3) yi*(t) и проверяем ограничение. Итерационную процедуру

заканчиваем, когда будет выполнено ограничение (см. таблицу ниже).

Детерминированная динамическая однопродуктовая модель управления запасами

В данной модели спрос и другие стоимостные характеристики изменяются во времени. Разобьем весь период управления T на m интервалов (месяц, неделя), j=1, 2,…,m. Для каждого интервала должны быть заданы (или спрогнозированы):

j – спрос на продукцию в интервал j времени, Kj – затраты на размещение заказа,

hi – затраты на хранение одной единицы продукции в единицу времени,

qi – цена продукции в интервал j времени.

Кроме этого, необходимо задать уровень запасов на начало планового срока – P0 (j=1).

В модели не допускается дефицита, а время выполнения заказа (L) считается неизменным.

143

Ставится задача определения оптимального размера заказа в каждый из интервалов – y*j (j=1, 2,..., m), причем в некоторые интерва-

Целевая функция на отдельном интервале времени представляет собой затраты Fj ( j , Kj ,hj ,qj , Pj , yj ) , в зависимости от количества

запасов на начало периода Pj решается вопрос о размере заказа yj. Затраты в этот интервал времени определяются по формуле:

модель).

Интегральная целевая функция имеет вид:

где Fj – затраты на функционирование системы управления запаса-

ми в интервал j.

Поставленная задача является сложной комбинаторной, но так как интегральная целевая функция представляет собой сумму, то для ее минимизации можно использовать динамическое программирование

[2].

3.3. Вероятностные модели управления запасами

M( ). Далее рассматриваются однопродуктовые вероятностные модели.

Упрощенная вероятностная модель

Будем считать, что время выполнения заказа (L) – постоянная величина. Обозначим через z суммарный спрос за время L, тогда f(z)

144

– плотность функции распределения вероятностей суммарного спроса, а F(z) – функция распределения вероятностей суммарного спроса.

На рис. 3.11 представлено изменение уровня запасов в вероятностных системах, РЗ – уровень резервного запаса.

P

Точки заказа

Рис. 3.11. График уровня запасов в вероятностных системах

Требуется определить РЗ при условии, что вероятность дефицита не больше, чем , т.е. P(z РЗ M(z)) .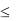

Используя заданную функцию распределения вероятностей, определяем квантиль z , соответствующий вероятности 1- .

Искомый уровень запасов определяется в соответствии со следующим выражением: РЗ z M(z) .

Пример.

Дано: L = 4 недели – время выполнения заказа, плотность

уровень резервного запаса, при условии, что вероятность возможного дефицита 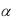не более 0,2.

Решение.

145

Математическое ожидание суммарного спроса за время выполне-

Находим квантиль z , соответствующий вероятности 1- =0,8. По таблице нормального распределения F(Х )=0,8, Х =0,9.

Так как Х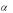соответствует нормированной случайной величине, то

Чтобы определить y* (уровень оптимального заказа), воспользуемся формулой Уилсона (3.1), подставив в нее M( ) (в этом заключа-

ется упрощенность модели):

y* 2KM( ) .

h

Отметим, что если L – случайная величина, и задана (L) – плотность функции распределения времени выполнения заказа, и, кроме того, если задана g(z/L) (условная функция плотности распределения спроса за время L), то безусловная функция плотности распределения f(z) определяется в соответствии с выражением:

f (z) g(z / L) (L)dL.

0

Имея f(z), можно определить необходимый резервный уровень запаса.

Вероятностная модель с контролем уровня запаса

В данной модели точка заказа определяется оптимальным уровнем резервного запаса R, который надо определить. Кроме этого, необходимо определить и оптимальный размер заказа y*.

Допущения, принятые в модели:

146

а) L – случайная величина;

б) плотность функции распределения вероятностей спроса f( ) за время выполнения заказа L не зависит от момента заказа;

в) неудовлетворенный спрос накапливается; г) в любой момент времени имеется не более одного невыполнен-

ного заказа.

В качестве исходных данных дано:

пределения спроса за время выполнения заказа; D – ожидаемый годовой спрос;

h – затраты на хранение в единицу времени на одну единицу продукции;

K – затраты на размещение заказа;

P – потери от дефицита одной единицы продукции.

Составим целевую функцию системы управления запасами, Dy –

количество заказов, которые будут сделаны в течение года. Целевая функция для оптимизации включает три составляющие:

147

Чтобы найти оптимальные значения y и R, возьмем частные про-

где g(x) – произвольная функция. Тогда, с учетом (3.5),

148

f (z)dz .

R

Таким образом, для определения оптимальных y и R необходимо решить следующую систему уравнений: