1.5. Метод Рунге-Кутта
Наиболее популярными среди классических явных одношаговых методов являются методы Рунге – Кутты. Метод Эйлера и его модификации можно рассматривать как простейших представителей этого класса методов.
Рассмотрим задачу Коши
(1.5) в общем случае на неравномерной
сетке
.
Для получения формулы нахождения
последующего значения
разложим решение
при
относительно точки
по формуле Тейлора на промежутке
:
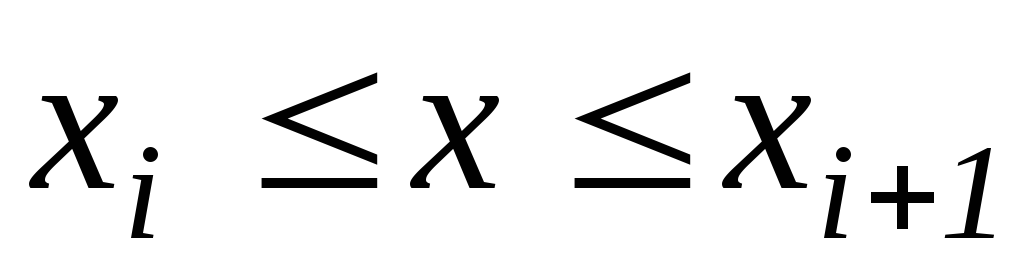(1.26)
Здесь последнее слагаемое
– это остаточный член разложения,
включающий элементы разложения выше
порядка
.
Входящие в правую часть производные
можно определить, дифференцируя уравнение
(1.25) требуемое число раз. Чем больше
членов разложения используется для
вычисления, тем точнее будет приближение
и тем выше порядок схемы. Однако
рассчитывать производные путем
дифференцирования правой части уравнения
(1.25) на практике крайне невыгодно. Поэтому
Рунге и Кутта независимо друг от друга
предложили более удобную и рациональную
форму представления численного решения,
при использовании которой дифференцировать
функцию
не требуется.
Наибольшее распространение в вычислительной практике нашел метод Рунге-Кутта четвертого порядка, для которого приближенное решение описывается выражением:
(1.27)
где
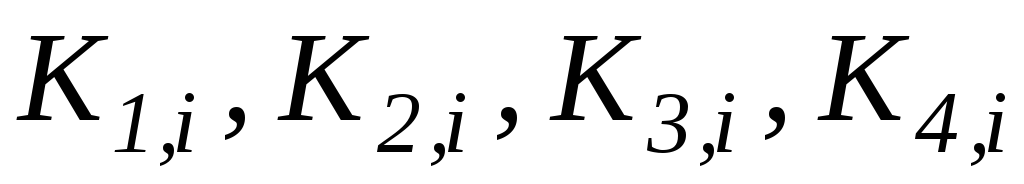- коэффициенты схемы Рунге-Кутта. Они
подбираются таким образом, чтобы
выражение для
согласовывалось с формулой Тейлора
вплоть до членов степени, которая
определяет порядок схемы.
Для схемы четвертого порядка данные коэффициенты определяют с помощью выражений:
(1.28)
Метод Рунге-Кутта позволяет
контролировать ошибку вычисления на
шаге. Существует грубая и точная оценки
ошибок. При точной оценке проверяется
разность по модулю значений
на каждом из четырех этапов его уточнения
с полученным общим решением. Это значение
сравнивается с заданной величиной
.
Данный способ контроля точности является
весьма затратным.
При грубой оценке, если выполняется соотношение
,
(1.29)
то шаг следует уменьшить. Если же соотношение не выполняется, то шаг можно оставить неизменным и даже попытаться его увеличить.
Метод Рунге-Кутта легко обобщается и на системы дифференциальных уравнений.