1. СТРУКТУРНЫЕ СХЕМЫ И ХАРАКТЕРИСТИКИ ИХ ЭЛЕМЕНТОВ

1.1. Основные положения

Основой для получения дифференциальных уравнений служит знание физических закономерностей протекания процессов в различ­ных элементах системы. Однако таких элементов может быть много и связи между ними могут быть различными. Поэтому часто прибегают к структурному изображению системы, на котором схематиче­ски показывают различные ее элементы (звенья) и связь между ними. Такое изображение системы, где в отличие от схемы замещения вни­мание обращено на взаимную связь элементов, а не на их содержа­ние, называется структурной схемой системы.

Структурные схемы позволяют более наглядно изучить влияние взаимодействия элементов системы на ее устойчивость и переходные процессы. Одновременно они выявляют ряд общих черт в задачах, которые при непосредственном описании в виде дифференциальных уравнений были бы незаметны, а также позволяют установить некоторые общие закономерности.

Структурная схема называется разомкнутой, если цепь прохо­ждения сигналов разомкнута, т.е. выходная величина не связана с входной, или, как говорят, нет обратной связи. Для регулируемых систем они всегда замкнуты и, как правило, являются сложными. Эти схемы могут быть составлены либо на основании записанной системы дифференциальных уравнений, либо на основании сведений о функциях отдельных элементов системы и взаимной связи между ними. Данные схемы широко применяются для изучения процессов в системах автоматического регулирования.

Основной частью структурной схемы является некоторый объект, который имеет некоторые свои особенности (рисунок 1.1)

Рисунок 1.1 – Основная часть структурной схемы

Здесь - входной сигнал объекта, а - выходной сигнал или реакция объекта. Объект представляет собой совокупность звеньев, которые соединяются между собой с помощью связей таким образом, чтобы реальный объект представить в виде определенной совокупности типовых звеньев. Соотношение выходного и входного сигналов объекта, выраженное в операторной форме, называется передаточной функцией объекта

(1.1)

Аналогично определяются передаточные функции и отдельных типовых звеньев, входящих в структурную схему. Зная передаточные функции отдельных звеньев, можно определить расчетным путем и передаточную функцию сложной системы в целом.

1.2. Элементарные звенья и их передаточные функции

Наиболее характерными звеньями регулируемой электрической системы, как и большинства регулируемых систем, являются: усилительное (безынерционное), инерционное (апериодическое), дифференцирующее, интегрирующее, запаздывающее, колебательное, суммирующее. Каждое звено харак­теризуется своей передаточной функцией, связывающей изображения входной и выходной величин, которая полностью опре­деляет динамические свойства звена. Рассмотрим передаточ­ные функции элементарных звеньев.

1. Усилительное (безынерционное или пропорциональное) звено (риунок 1.2 а) является самым простым звеном, выходная величина которого прямо пропорциональна входной.

а б

Рисунок 1.2 – Пропорциональное звено

Уравнение такого звена

, (1.2)

где - коэффициент усиления, может быть как размерным, так и безразмерным.

Передаточная функция звена

. (1.3)

Примером такого звена является делитель на­пряжения (рисунок 1.2 б).

Инерционное (апериодическое) звено (рис. 1.3 а) одно из са­мых распространенных в автоматически регулируемых системах, описывается дифференциальным уравнением

, (1.4)

где - постоянная времени;

- коэффициент усиления.

а б в

Рисунок 1.3 – Инерционное (апериодическое) звено

Передаточная функция этого звена имеет вид

. (1.5)

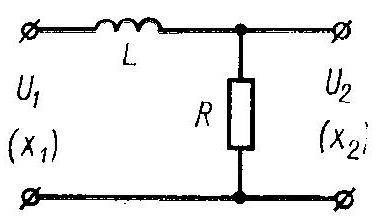
В установившемся режиме инерционное звено имеет те же пара­метры, что и усилительное. Примерами такого звена (рисунок 1.3 б, в) являются четырехполюсники, содержащие индуктивность или емкость.

Дифференцирующее звено (рисунок 1.4 а), называемое иногда реальным, определяется дифференциальным уравнением

, (1.6)

а б в

Рисунок 1.4 – Дифференцирующее звено

Передаточная функция такого звена

. (1.7)

Установившееся значение выходной величины равно нулю. Дифференцирующее звено с (при ) имеет передаточную функцию

. (1.8)

и называется идеальным дифференцирующим звеном.

Примерами такого звена (рисунок 1.4 б, в) являются четырехполюсники, содержащие соответствующим образом включенные активные и реактивные сопротивления.

Интегрирующее звено (рисунок 1.5 а) определяется уравнением

, (1.9)

т.е. входная величина пропорциональна интегралу от входной

а б в

Рисунок 1.5 – Интегрирующее звено

Передаточная функция этого звена равна

. (1.10)

Примерами такого звена являются электрическая индуктивность и емкость (рисунок 1.5 б, в).

Запаздывающее звено определяется уравнением

. (1.11)

Передаточная функция такого звена имеет вид

. (1.12)

Примерами такого звена являются различные схемные решения линий задержки.

Колебательное звено (рисунок 1.6 а) описывается дифференциальным уравнением второго порядка

, (1.13)

где - коэффициент демпфирования;

- коэффициенты усиления;

- входной и выходной сигналы.

Разделим уравнение (1.13) на , получим

, (1.14)

где - коэффициент затухания,

; (1.15)

- собственная частота колебаний звена (без демпфирования)

. (1.16)

а б

Рисунок 1.6 – Колебательное звено

В операторной форме уравнение (1.14) запишется в виде

, (1.17)

откуда

, (1.18)

Колебательное звено является важнейшим элементом структурных схем при изучении электромеханических переходных процессов в электрических системах. Примером такого звена может служить электрический колебательный контур, приведенный на рисунке 1.6 б. Здесь

; ; .

Суммирующее звено с выходной величиной и входными величинами , где

. (1.19)

На схемах суммирующее звено изображают либо в виде кружка (рисунок 1.7 а), либо в виде вертикальной черты (рисунок 1.7 б), к которым, с одной стороны, подходят входные величины , а с другой стороны, отходит выходная величина .

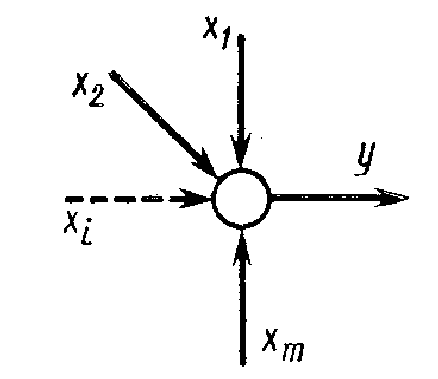
а б

Рисунок 1.7 – Суммирующее звено

1.3. Передаточная функция системы элементарных звеньев

Передаточная функция разомкнутой цепи зави­сит от вида соединений звеньев.

Последовательным соединением звеньев называется такое, при ко­тором выходная величина предшествующего звена является входной величиной последующего звена (рисунок 1.8)

Рисунок 1.8 – Последовательное соединение элементарных звеньев

Эту схему можно описать следующей системой уравнений

. (1.20)

Подставим в последнее уравнение значение из предпоследнего уравнения. В полученное уравнение подставим значений из следующего уравнения, и т.д. В результате получим

, (1.21)

откуда

. (1.22)

Следовательно, передаточная функция последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев.

Параллельным соединением звеньев называется такое, при котором входной величиной всех звеньев является одна и та же величина, а выходные величины суммируются (рисунок 1.9)

Рисунок 1.9 – Параллельное соединение элементарных звеньев

Эту схему можно описать следующей системой уравнений

. (1.23)

По определению данной схемы . С учетом этого и на основании системы уравнений (1.23) получим

. (1.24)

Следовательно, передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев.

На практике структурные схемы представляют собой совокупность последовательного и параллельного соединения звеньев, т.е. представляют собой схемы смешанного вида. Для них составляют сложное выражение передаточной функции системы, используя соотношения (1.22) и (1.24). Затем выражение приводится к общему знаменателю и производится приведение подобных членов. В результате передаточная функция разомкнутой системы, представляющей собой совокупность последовательно и параллельно соединенных звеньев, будет представлять собой соотношение двух многочленов

. (1.25)

В большинстве случаев степень многочлена числителя меньше степени многочлена знаменателя. Уравнение является характеристическим уравнением разомкнутой системы.

1.4. Структурные схемы с обратной связью

Для изменения статических и динами­ческих характеристик системы вводятся обратные связи. Эти изменения зависят от способа соединения и типа звеньев, включенных в цепь обратной связи.

Пусть некоторое звено с передаточной функцией охвачено обратной связью, т.е. к выходу этого звена присоединяется второе звено с передаточной функцией , выход которого подается на вход первого звена с положительным знаком (положительная обратная связь) или с отрицательным знаком (отрицательная обратная связь) (рисунок 1.10)

Рисунок 1.10 – Структурная схема с обратной связью

Найдем передаточную функцию эквивалентного звена, полученного из первого звена, охваченного обратной связью с помощью второго звена. Вход эквивалентного звена обозначим через , выход – . Чтобы полу­чить функцию , в которой

, (1.26)

запишем соотношения между переменными на входе и выходе отдель­ных звеньев:

. (1.27)

где знак «+» соответствует положительной обратной связи, а знак «–» - отрицательной.

Учитывая эти соотношения, последовательно получим:

;

;

, (1.28)

откуда

, (1.29)

где знак «–» соответствует положительной обратной связи, а знак «+» - отрицательной.

Часто в системах автоматического регулирования охватывают обратной связью инерционное зве­но, чтобы получить новое эквивалент­ное инерционное звено с измененными параметрами. В качестве об­ратной связи применяют либо безынерционное звено – такая обратная связь называется жесткой, либо дифференцирующее звено – такая обратная связь называется гибкой.

Рассмотрим инерционное звено, охваченное жесткой обратной связью. Передаточная функция звена с отрицательной обратной связью имеет вид

. (1.30)

Найдем передаточную функцию эквивалентного звена с помощью выражения (1.29)

, (1.31)

где - коэффициент усиления эквивалентного инерционного звена, равный

; (1.32)

- постоянная времени эквивалентного инерционного звена

. (1.33)

Таким образом, при охвате инерционного звена жесткой обратной связью получа­ется новое инерционное звено с уменьшенными коэффициентом уси­ления и постоянной времени. Отношение коэффициента усиления к постоянной времени остается неизменным. В системах автоматиче­ского регулирования возбуждения (АРВ сильного действия) синхрон­ных машин часто возбудитель охватывают такой связью для уменьшения его постоянной времени.

В некоторых случаях инерционное звено охватывают жесткой обратной связью с коэффициентом усиления . Тогда согласно (1.32)

, (1.34)

т.е. коэффициент усиления системы определяется обратной величи­ной коэффициента усиления элемента обратной связи.

Теперь рассмотрим инерционное звено, охваченное гибкой отрица­тельной обратной связью. Передаточная функция звена об­ратной связи в этом случае имеет вид

, (1.35)

Часто параметры звена обратной связи выбирают такими, чтобы , т.е. применяют идеальное дифференцирующее звено с передаточной функцией . Для такой обратной связи найдем передаточную функцию эквивалентного звена с помощью выражения (1.29)

, (1.36)

где

. (1.37)

Таким образом, при охвате инерционного звена гибкой обратной связью получа­ется новое инерционное звено с неизменным коэффициентом усиле­ния и увеличенной постоянной времени. Гибкая отрицательная обратная связь не меняет статические характеристики инерционного звена, меняя его динамические характеристики.