Матмодели. Лекции, литература, задание 1 лаба / Тема 2 матмоделей

1. ОБЩИЕ СВЕДЕНИЯ

1.1. Основные положения теории графов

Конфигурацию схемы замещения электрической системы можно отобразить в виде графа. Граф представляет собой множество вершин (узлов) и ребер (ветвей), соединяющих некоторые (а может быть и все) пары вершин. Любая часть графа называется подграфом. Совокупность ребер, соединяющих две произвольные вершины, образует подграф, определяемый как путь графа. Если начальная и конечная вершины пути графа совпадают, то этот путь графа является замкну­тым и образует контур.

Если в графе можно выбрать путь, который соединяет его любые две вершины, то этот граф является связанным; если нельзя – то несвязанным. Если ребра графа имеют фиксированные направления, то этот граф называется направленным. Каждое ребро направленного графа имеет начальную и конечную вершины; его направление при­нимается от первой вершины ко второй.

Схема замещения электрической системы обычно является связан­ным графом. Она состоит из ветвей (ребер), соединенных в узлы (вершины). Ветви образуют цепочки (пути графа), которые могут быть замкнутыми. Все величины, характеризующие состояние ветвей (токи, ЭДС, падения напряжения), должны иметь определенное направление, так как без этого не может быть рассчитан режим данной схемы. В связи с этим целесообразно каждой ветви схемы придать определенное, произвольно выбранное направление. Таким образом, схема заме­щения системы обычно является связанным направленным графом, ребрами которого служат ветви, а вершинами — узлы.

На рис. 1.1 приведен пример связанного направленного графа, у которого выбраны направления ветвей, а также указаны номера ветвей и узлов. На рис. 1.2 изображена часть этого графа – подграф, являющийся несвязанным, так как, например, нет пути графа, связывающего вершины и .

Рисунок 1.1 – Пример направленного связанного графа

Рисунок 1.2 – Пример несвязанного подграфа

При изображении схем в виде графов нет надобности в специаль­ных обозначениях сопротивлений и ЭДС. Ветви графически изобра­жаются прямой с указанием их направлений. Таким образом, направление ветви от начального узла к конечному узлу одновременно является положительным направлением и для всех участвующих величин – ЭДС , тока и падения напряже­ния . Любая из этих величин может получиться положительной или отрицательной по отношению к принятому направлению.

Для направленного графа могут быть определены:

1) матрица соединений ветвей в узлах (первая матрица инциденций);

2) матрица соединений ветвей в независимые кон­туры (вторая матрица инциденций),

Обе эти матрицы служат для обобщенного аналитического представления графа. Матрица соединений ветвей в узлах – это прямоугольная матрица, число строк которой равно числу вершин графа , а число столбцов – числу ребер . Она обозначается следующим образом:

; ; . (1.1)

При этом номера строк соответствуют номерам вершин, а но­мера столбцов – номерам ребер. Элементы матрицы могут при­нимать одно из трех значений:

, если узел является начальной вершиной ветви ;

, если узел является конечной вершиной ветви ;

, если узел не является вершиной ветви ;

Каждая строка матрицы показывает, какими вершинами соответ­ствующие ветви присоединяются к данному узлу схемы; каждый стол­бец – какие узлы являются начальной и конечной вершинами данной ветви. Следовательно, в каждом столбце матрицы может быть только одна положительная и одна отрицательная единицы, осталь­ными элементами являются нули. Следовательно, сумма всех строк этой матрицы по столбцам должна давать нулевую строчную матрицу:

, (1.2)

где – единичная строка.

Если выделить строку, соответствующую некоторому узлу, при­нятому за балансирующий, причем номер ее принять последним, то это условие запишется в следующем виде:

, (1.3)

откуда

. (1.4)

Здесь – матрица соединений для схемы без балансирующего узла; – матрица соединений для балансирующего узла.

Полученный результат означает, что одна из строк матрицы может быть образована суммированием прочих строк по столбцам и изменением знаков всех элементов суммарной матрицы на обрат­ные. Поэтому для практических расчетов достаточно пользоваться матрицей , по которой может быть восстановлена вся схема. В случае необходимости матрица может быть определена по выражению

. (1.5)

Для направленного графа, показанного на рисунке 1.1, матрица имеет вид:

Выбрав узел в качестве балансирующего, получим матрицу из путем исключения последней строки.

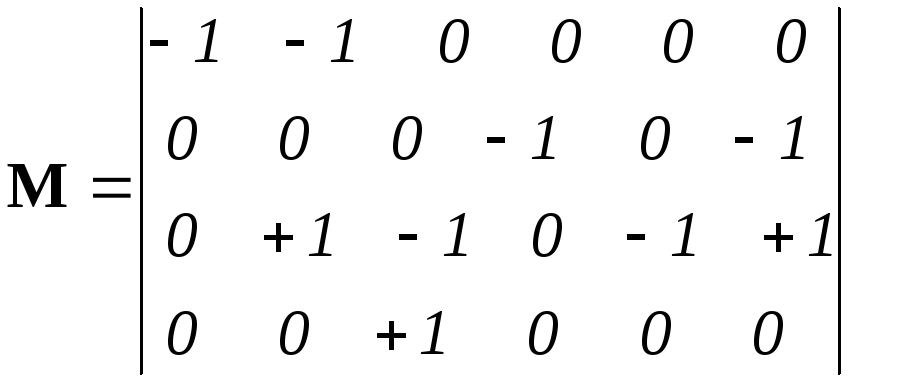
По этой матрице можно восстановить исключенную строку, которая является матрицей :

Матрица соединений ветвей в независимые контуры – это прямоугольная матрица, число строк которой равно числу независимых контуров графа , а число столбцов – числу ветвей . Она обозна­чается следующим образом:

; ; . (1.6)

При этом номера строк соответствуют номерам независимых контуров, а номера столбцов – номерам ветвей.

Элементы матрицы определяются следующим образом:

, если ветвь входит в контур и их направления совпадают;

, если ветвь входит в контур и их направления противоположны;

, если ветвь не входит в контур .

Каждая строка матрицы показывает, какие ветви входят в состав соответствующего независимого контура и какое направле­ние имеют относительно направления контура. Каждый столбец той же матрицы показывает, в состав каких независимых контуров вхо­дит данная ветвь и совпадает ли ее направление с направлениями этих контуров.

Для направленного графа, показанного на рисунке 1.1, матрица имеет вид:

Матрицы и дают возможность записать уравнения состоя­ния электрической цепи в матричной форме. Система взаимно неза­висимых уравнений первого закона Кирхгофа может быть представ­лена в виде:

, (1.7)

где , ; , – столбцы токов в ветвях и задающих токов в узлах соответственно.

Анало­гично, система взаимно независимых уравнений второго закона Кирх­гофа может быть записана в виде

, (1.8)

где , – столбец падений напряжений на вет­вях схемы.

Чтобы ввести в уравнения второго закона Кирхгофа токи в вет­вях схемы замещения, воспользуемся законом Ома. Для сети про­извольной конфигурации, содержащей ветвей, между которыми отсутствует взаимоиндуктивная связь, этот закон выражается мат­ричным уравнением:

, (1.9)

где , – диагональная матрица сопротив­лений ветвей; , – столбец ЭДС в ветвях.

Подставляя (1.9) в (1.8), получим матричное уравнение второго закона Кирхгофа:

,

или

, (1.10)

где – столбец контурных ЭДС, представляющих собой алгебраические суммы ЭДС ветвей, входящих в каждый независимый контур.

Объединяя матричные уравнения (1.7) и (1.10) в общую си­стему, получим обобщенное уравнение состояния электрической цепи, вид которого не зависит от ее конфигурации и числа элементов:

. (1.11)

Эти уравнения можно объединить в одно, если матрицы и рассматривать как блоки одной объединенной матрицы пара­метров схемы замещения системы:

, (1.12)

а матрицы и рассматривать как блоки одной объединенной матрицы исходных параметров режима:

. (1.13)

При этом обобщенное уравнение состояния принимает вид

. (1.14)

Здесь матрица является квадратной и в обычных условиях неособенной, поэтому полученное уравнение состояния можно ре­шить относительно матрицы токов ветвей.

Для формирования обобщенного уравнения состояния (1.14) необходимо предварительно определить матрицы соединений и , которые в аналитической форме отображают конфигурацию схемы замещения электрической системы.

Составление матрицы для схемы любой сложности не представляет труда. Для этого достаточно пронумеровать все узлы и ветви схемы замещения и в каждом столбце матрицы записать «+1» «-1» в тех строках, которые соответствуют соединяемым дан­ной ветвью узлам, а в остальных элементах этого столбца записать «0». Вычеркивая из полученной матрицы строку, соответствующую выбранному балансному узлу, получим матрицу .

Составить матрицу для сложных электрических систем в отли­чие от матрицы затруднительно, поскольку предварительно тре­буется выделить независимые контуры, количество которых может быть значительным. Кроме того, матрица в общем случае не содержит полной информации о конфигурации рассматриваемой системы, так как разомкнутые части схемы в ней не отражаются. Например, ветвь 3 на рисунке 1.1 представлена в матри­це нулевыми элементами и присоединение ее к любому дру­гому узлу не изменяет матрицу . Целесообразно формализовать процесс составления матрицы . Возможность этой формализации обусловлена тем, что матрица содержит исчерпывающую информацию о конфигурации схемы, в том числе и необходимую для составления матрицы . Установим аналитическую зависимость, связывающую эти матрицы.

Пусть необходимо определить падения напряжений на ветвях некоторой схемы. Обозначим вектор-столбец напряжений всех узлов схемы , . В этот вектор-столбец входят напряжения всех узлов, включая и балансирующий, которые определяются относительно любого узла, даже не входящего в схему (например, нейтрали, с которой узлы схемы могут не иметь связи). Часто узловые напряжения целесообразно определять как падения напряжения относительно балансирующего узла

, (1.15)

где - единичный столбец, при этом балансирующий узел в предполагается последним по номеру; , - вектор-столбец падений напряжений в узлах относительно балансирующего.

Тогда падения напряжения в ветвях определяются выражением:

. (1.16)

Подставляя в матричное уравнение второго закона Кирхгофа (1.8) выражение (1.16), получим

(1.17)

Поскольку данное условие справедливо при любой матрице , то, следовательно

(1.18)

Выражение (1.18) отображает общее топологическое свойство графа. В этом можно убедиться на вышеприведенном примере. Однако данное условие не позволяет непосредственно определить матрицу по известной матрице . Это объясняется тем, что для одной и той же электрической цепи существует несколько систем независимых контуров, т.е. одной матрице можно поставить в соответствие несколько матриц .

Однозначность в выделении системы независимых контуров, позволяющая получить матрицу по матрице , может быть дости­гнута при использовании таких понятий теории графов, как дере­во и хорды.

Деревом называется наимень­ший связанный подграф, содержа­щий все вершины графа. Такой подграф не содержит контуров. Иными словами, дерево – это ра­зомкнутая часть замкнутой схе­мы, которая соединяет все ее уз­лы. Число ветвей, входящих в со­став дерева схемы, на единицу меньше числа узлов всей схемы (). Меньшим числом ветвей нельзя соединить те же узлы.

Разомкнутая схема получает­ся путем исключения некоторых ветвей, входящих в независимые контуры исходной схемы. Оставшиеся ветви образуют дерево графа.

Ветви, не вошедшие в дерево схемы, называются хордами. Чис­ло хорд равно числу независимых контуров схемы (). Подграф, со­стоящий из хорд, может содер­жать контуры; он может полу­читься и несвязанным.

Одна и та же схема может быть разделена на дерево и хорды по-разному. Обычно число вариантов такого разделения получается достаточно большим. На рисунке 1.3 показаны некоторые возможные случаи разделения графа, изображенного на рисунке 1.1, на дерево и хорды.

Рисунок 1.3 – Возможные варианты разбиения графа на дерево и хорды

При этом некоторые из подграфов, состоящие из хорд, могут получиться несвязанными, могут содержать контура. В данном примере контуров нет, так как число хорд всего две. Для простых схем задача разбиения графа на дерево и хорды может быть выполнена вручную без особого труда. Для сложных схем эта задача выполняется с помощью ЭВМ, для этого разработаны эффективные алгоритмы.

После перестановки строк и столбцов, матрица преобразуется к виду

, (1.19)

где - подматрица дерева графа; - подматрица хорд графа.

Аналогично можно разделить на блоки и матрицу

, (1.20)

Подставляя (1.19) и (1.20) в (1.18), получим

. (1.21)

Матрица , а следовательно и , является квадратной порядка () и неособенной. Поэтому, умножая обе части выражения (1.21) на , найдем

. (1.22)

Матрицу можно задать равной единичной матрице (), для этого необходимо задаться такой системой контуров, которые бы характеризовались следующими свойствами:

а) каждый из контуров замыкается одной хордой, т.е. каждая хорда входит только в один контур;

б) последовательности нумерации хорд и контуров одинаковы;

в) направления обхода контуров и замыкающих их хорд одинаковы.

Такие контуры называются базисными. Они являются взаимно независимыми, так как в каждый из них одна хорда, не входящая ни в какой другой контур. Тогда для базисных контуров выражение (1.22) примет вид

. (1.23)

Итак, разделение матрицы на блоки, соответствующие дереву и хордам графа, позволяет однозначно определить матрицу для системы базисных контуров, отвечающих данному дереву. Тем са­мым задача формирования уравнений состояния электрической цепи произвольной конфигурации вида (1.12) сводится к составлению матрицы , разделению ее на блоки , и выполнению над ними стандартных операций.

1.2. Метод узловых уравнений

Задачей расчета установившегося режима электрической системы является определение токов в ветвях схемы замещения, напряжений в ее узловых точках и соответствующих им мощностей. В общем случае для замкнутой схемы замещения эта задача решается следующим образом. Составляется обобщенное уравнение состояния (1.14), которое решается относительно токов в ветвях. По найденной матрице определяются падения напряжения на вет­вях схемы согласно уравнению закона Ома (1.9). Далее нахо­дятся напряжения узлов относительно балансирующего .

Изложенная последовательность расчета параметров установив­шегося режима электрической системы характеризуется тем, что на этапе определения токов в ветвях решается система урав­нений порядка , где – число ветвей. Если же использовать другую последовательность, т. е. начинать расчет с определения напряжений в узлах схемы относительно балансирующего (матрицы ), то порядок решаемой системы уравнений будет равен . Поскольку число ветвей превышает на число независимых контуров (), то для сложных замкнутых схем можно получить существенное понижение порядка решаемой системы урав­нений.

Система, состоящая из () уравнений, связывающих напря­жения узлов относительно балансирующего с задающими токами в узлах и ЭДС в ветвях, называется системой узловых уравнений. Она широко применяется в практике расчетов установившихся ре­жимов сложных электрических систем. Система узловых уравнений может быть получена следующим образом:

а) подставляя в уравнение (1.16), связывающее матрицы и , выражение из (1.9), получим

; (1.24)

б) разрешив полученное уравнение относительно (что возможно, поскольку – квадратная и неособенная матрица), будем иметь

; (1.25)