Матмодели. Лекции, литература, задание 1 лаба / Тема 6 матмоделей

1. МЕТОДЫ ОПТИМИЗАЦИИ

1.1. Основные положения

Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т.п. В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу. При решении инженерных задач их принято называть проектными параметрами. В качестве проектных параметров могут быть, в частности, значения линейных размеров объекта, массы, температуры и т. п. Число проектных параметров характеризует размерность (и степень сложности) задачи оптимизации.

Выбор оптимального решения или сравнение двух альтернативных решений проводится с помощью некоторой зависимой величины (функции), определяемой проектными параметрами. Эта величина называется целевой функцией (или критерием качества). В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет минимум (или максимум). Таким образом, целевая функция – это глобальный критерий оптимальности в математических моделях, с помощью которых описываются инженерные или экономические задачи.

Целевую функцию можно записать в виде

. (1.1)

Примерами целевой функции, встречающимися в инженерных и экономических расчетах, являются прочность или масса конструкции, мощность установки, объем выпуска продукции, стоимость перевозок грузов, прибыль и т.п.

В случае одного проектного параметра ( = 1) целевая функция (1.1) является функцией одной переменной, и ее график – некоторая кривая на плоскости. При = 2 целевая функция является функцией двух переменных, и ее график – поверхность в трехмерном пространстве. Следует отметить, что целевая функция не всегда может быть представлена в виде формулы. Иногда она может принимать только некоторые дискретные значения, задаваться в виде таблицы и т.п. Во всех случаях она должна быть однозначной функцией проектных параметров. Целевых функций может быть несколько. Например, при проектировании изделий машиностроения одновременно требуется обеспечить максимальную надежность, минимальную материалоемкость, максимальный полезный объем (или грузоподъемность). Некоторые целевые функции могут оказаться несовместимыми. В таких случаях необходимо вводить приоритет той или иной целевой функции.

Можно выделить два типа задач оптимизации – безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (1.1) от действительных переменных и определении соответствующих значений аргументов на некотором множестве -мерного пространства. Обычно рассматриваются задачи минимизации; к ним легко сводятся и задачи на поиск максимума путем замены знака целевой функции на противоположный.

Условные задачи оптимизации, или задачи с ограничениями – это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве . Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.

Ограничения-равенства выражают зависимость между проектными параметрами, которая должна учитываться при нахождении решения. Эти ограничения отражают законы природы, наличие ресурсов, финансовые требования и т. п.

В результате ограничений область проектирования , определяемая всеми проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи. Число ограничений-равенств может быть произвольным. Их можно записать в виде

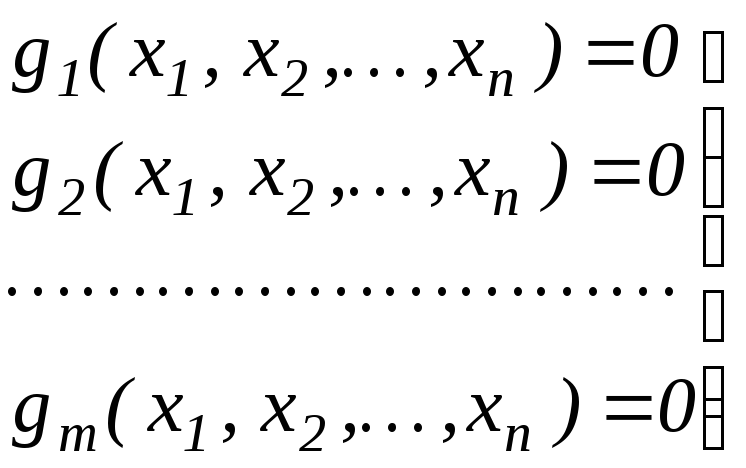(1.2)

В ряде случаев из этих соотношений можно выразить одни проектные параметры через другие. Это позволяет исключить некоторые параметры из процесса оптимизации, что приводит к уменьшению размерности задачи и облегчает ее решение. Аналогично могут вводиться также ограничения-неравенства, имеющие вид

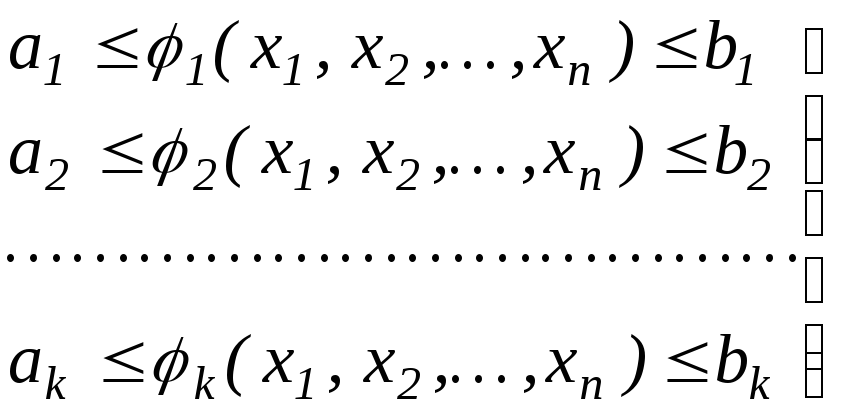. (1.3)

Следует отметить особенность в отыскании решения при наличии ограничений. Оптимальное решение здесь может соответствовать либо локальному экстремуму (максимуму или минимуму) внутри области проектирования, либо значению целевой функции на границе области. Если же ограничения отсутствуют, то ищется оптимальное решение на всей области проектирования, т.е. глобальный экстремум.

Теория и методы решения задач оптимизации при наличии ограничений составляют предмет исследования одного из важных разделов прикладной математики – математического программирования.

Рассмотрим пример постановки задачи. Пусть требуется спроектировать контейнер в форме прямоугольного параллелепипеда объемом , причем желательно израсходовать на его изготовление как можно меньше материала.

При постоянной толщине стенок последнее условие означает, что площадь полной поверхности контейнера должна быть минимальной. Если обозначить через длины ребер контейнера, то задача сведется к минимизации функции

.

Эта функция в данном случае является целевой, а условие - ограничением-равенством, которое позволяет исключить один параметр:

;

,

откуда

. (1.4)

Задача свелась к минимизации функции двух переменных. В результате решения задачи будут найдены значения проектных параметров , а затем и . В приведенном примере фактически получилась задача безусловной оптимизации для целевой функции (1.4) в положительной области параметров, поскольку ограничение-равенство было использовано для исключения параметра .

Вместе с тем можно усложнить рассматриваемую задачу и поставить дополнительные условия. Например, потребуем, чтобы данный контейнер имел длину не менее 2 м. Это условие запишется в виде ограничения-неравенства на один из параметров, например

. (1.5)

Таким образом, мы получили следующую условную задачу оптимизации: минимизируя функцию (1.4) и, учитывая ограничение-неравенство (1.5), найти оптимальные значения параметров плана .

1.2. Задачи с ограничениями. Линейное программирование

Решение задач математического программирования значительно более трудоемко по сравнению с задачами безусловной оптимизации. Ограничения типа равенств или неравенств требуют их учета на каждом шаге оптимизации. Одним из направлений в методах решения задач математического программирования является сведение их к последовательности задач безусловной минимизации. К этому направлению относится, в частности линейное программирование, изучающее задачи оптимизации, в которых, целевая функция является линейной функцией проектных параметров, а ограничения задаются в виде линейных уравнений и неравенств.

Стандартная (каноническая) постановка задачи линейного программирования формулируется следующим образом: найти значения переменных , которые:

1) удовлетворяют системе линейных уравнений

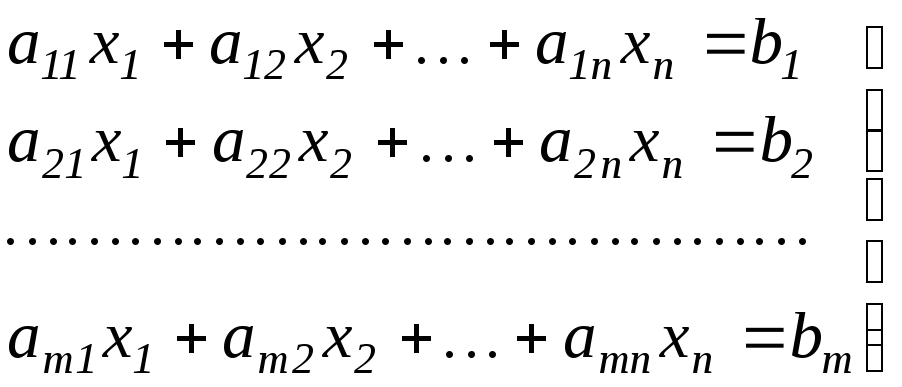(1.6)

2) являются неотрицательными, т. е.

(1.7)

3) обеспечивают наименьшее значение линейной целевой функции

. (1.8)

Всякое решение системы уравнений (1.6), удовлетворяющее системе неравенств (1.7), называется допустимым решением. Допустимое решение, которое минимизирует целевую функцию (1.8), называется оптимальным решением.

Рассмотрим пример задачи линейного программирования (транспортную задачу).

Пример. Автобаза обслуживает три овощных магазина, причем товар доставляется в магазины из двух плодоовощных баз. Нужно спланировать перевозки так, чтобы их общая стоимость была минимальной.

Зададим исходные данные. Ежедневно вывозится с первой базы 12 т товара, со второй 15 т. При этом завозится в первый магазин 8 т, во второй 9 т, в третий 10 т. Стоимость перевозки 1 т товара (в рублях) с баз в магазины дается следующей таблицей 1.1

Таблица 1.1 – Стоимость перевозки 1 т товара, руб.

База	Магазин
	Первый	Второй	Третий
Первая	800	1100	900
Вторая	1000	700	1200

Решение. Обозначим через количество товара, который нужно доставить с первой базы соответственно в первый, второй и третий магазины, а через количество товара, который нужно доставить со второй базы в те же магазины. Эти значения в соответствии с исходными данными должны удовлетворять следующим условиям:

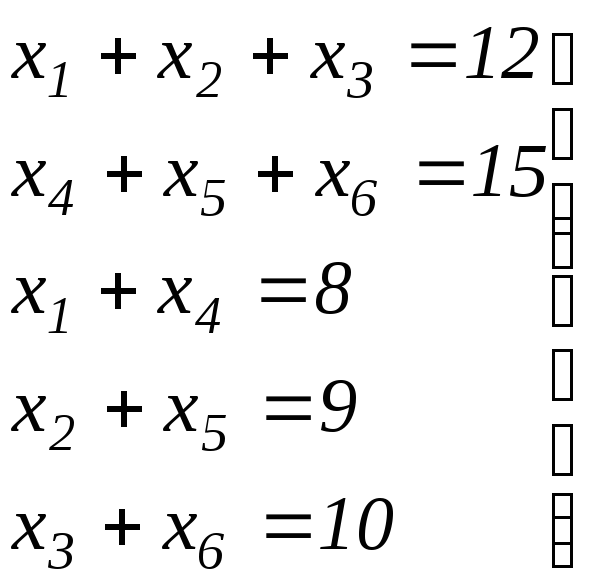. (1.9)

Первые два уравнения этой системы описывают количество товара, которое необходимо вывезти с первой и второй баз, а три последних – сколько нужно завезти товара в каждый магазин. К данной системе уравнений нужно добавить систему неравенств

, (1.10)

которая означает, что товар обратно с магазинов на базы не вывозится. Общая стоимость перевозок с учетом приведенных в таблице расценок выразится формулой

. (1.11)

Таким образом, мы пришли к типичной задаче линейного программирования: найти оптимальные значения проектных параметров , удовлетворяющих условиям (1.9), (1.10) и минимизирующих общую стоимость перевозок (1.11).

Из анализа системы уравнений (1.9) следует, что только первые четыре уравнения являются независимыми, а последнее можно получить из них (путем сложения первого и второго уравнений и вычитания из этой суммы третьего и четвертого уравнений). Поэтому фактически имеем систему:

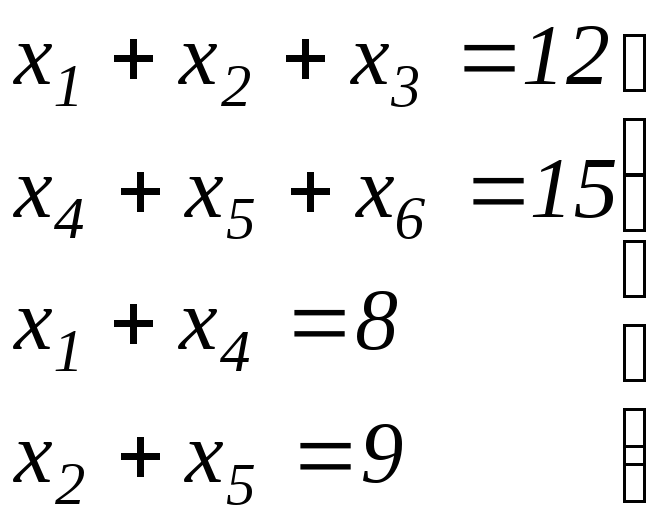. (1.12)

Число неизвестных на два больше числа уравнений, поэтому выразим через и все остальные неизвестные. Получим

. (1.13)

Поскольку в соответствии с (1.10) все проектные параметры должны быть неотрицательны, то с учетом (1.13) получим следующую систему неравенств:

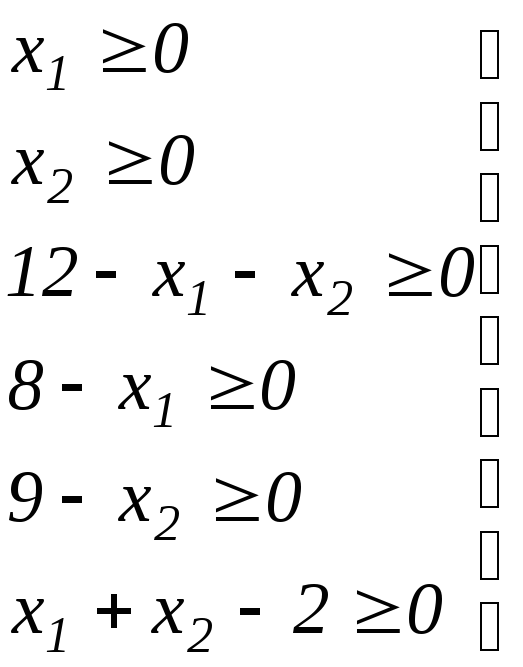. (1.14)

Эти неравенства можно записать в более компактном виде:

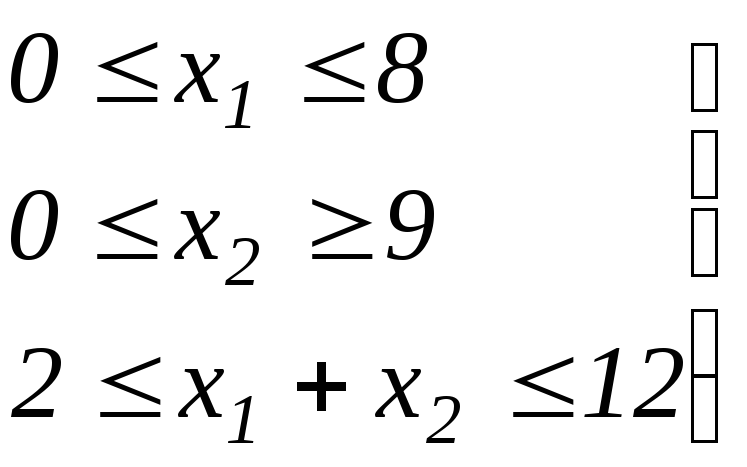. (1.15)

Данная система неравенств описывает все допустимые решения рассматриваемой задачи. Среди всех допустимых значений свободных параметров нужно найти оптимальные, минимизирующие целевую функцию . Формула (1.11) для нее с учетом соотношений (1.13) принимает вид

. (1.16)

Отсюда следует, что стоимость перевозок растет с увеличением значений и поэтому нужно взять их наименьшие допустимые значения. В соответствии с (1.15) . При минимальных значениях этих параметров . Исключая один из параметров, например, , получим . Тогда

. (1.17)

Очевидно, что стоимость перевозок будет минимальной, если величина примет наибольшее значение в рамках сделанного выше ограничения . Таким оптимальным, когда оба слагаемых неотрицательные, будет значение . Тогда , а оптимальные значения остальных проектных параметров можно найти по формулам (1.13): ; ; ; . В этом случае минимальная общая стоимость перевозок равна 22900 рублей. На рисунке 1.1 показана схема доставки товаров, соответствующая полученному решению. Числа указывают количество товара (в тоннах).

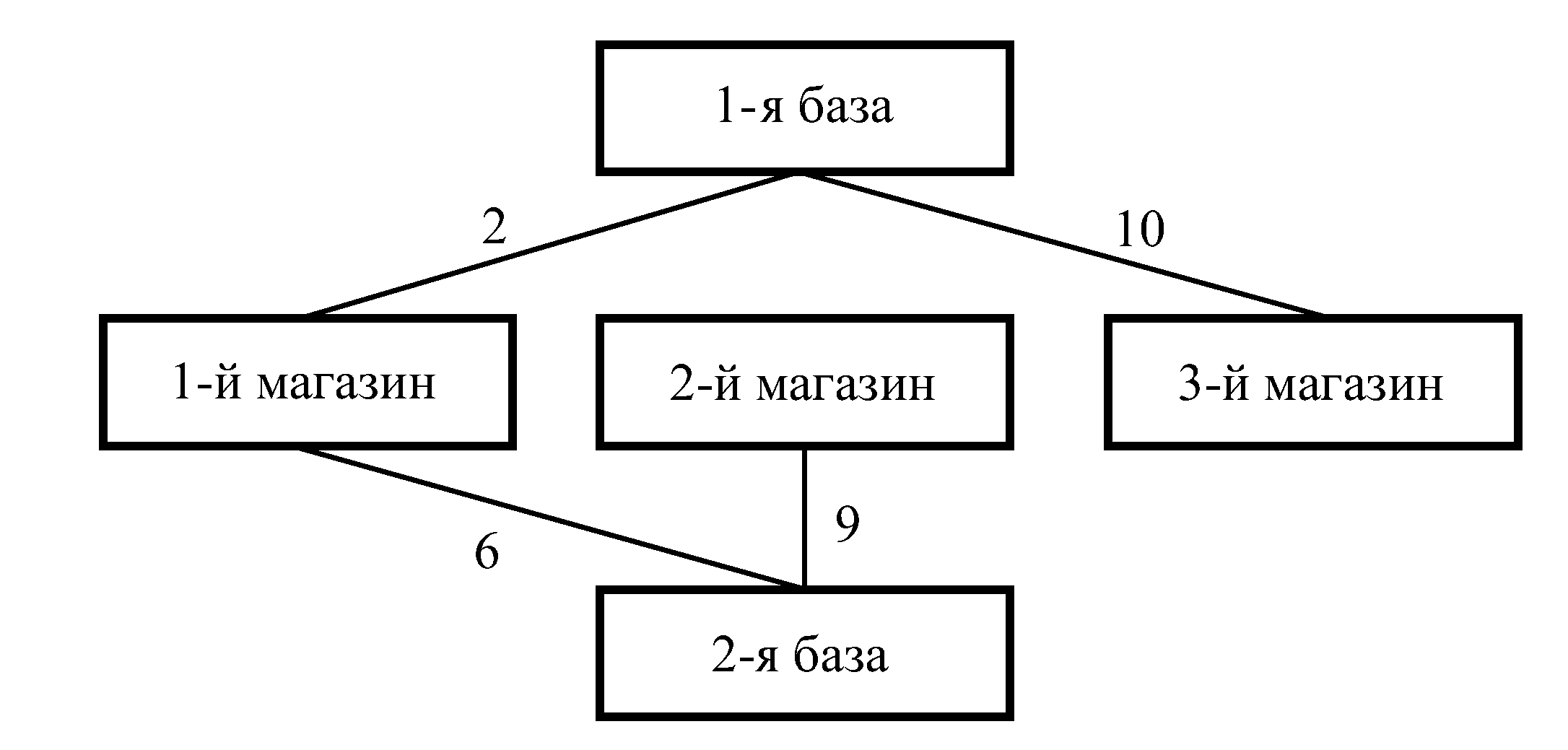
Рисунок 1.1 – Схема перевозок