
Матмодели. Лекции, литература, задание 1 лаба / Тема 1 матмоделей
.docОБЩИЕ СВЕДЕНИЯ
1.1. Методы решения нелинейных уравнений
Пусть дано нелинейное уравнение вида:
![]() ,
(1)
,
(1)
где
![]() - функция, определенная и непрерывная
на некотором промежутке. Требуется
найти корни уравнения, т.е. числа
- функция, определенная и непрерывная
на некотором промежутке. Требуется
найти корни уравнения, т.е. числа
![]() ,
,
![]() ,
которые при подстановке в данное
уравнение превращают его в числовое
равенство. При этом рассматриваются
только вещественные корни.
,
которые при подстановке в данное
уравнение превращают его в числовое
равенство. При этом рассматриваются
только вещественные корни.
В зависимости от вида уравнения число
корней может быть различным. Например,
уравнение
![]() имеет 4 корня, уравнение
имеет 4 корня, уравнение
![]() имеет бесконечное число корней, уравнение
имеет бесконечное число корней, уравнение
![]() имеет некоторое конечное число корней.
имеет некоторое конечное число корней.
Для решения данных уравнений применяют численные методы, которые являются приближенными с заданной степенью точности и состоят из двух этапов:
1. Находятся отрезки
![]() ,
внутри которых содержится один корень
,
внутри которых содержится один корень
![]() .
Этот этап называется отделением корней
или локализацией корней. По сути, на
данном этапе осуществляется грубое
нахождение корней
.
Этот этап называется отделением корней
или локализацией корней. По сути, на
данном этапе осуществляется грубое
нахождение корней
![]() .
.
2. Грубое значение каждого корня
![]() уточняется до заданной точности одним
из численных методов, в которых реализуется
последовательные приближения.
уточняется до заданной точности одним
из численных методов, в которых реализуется
последовательные приближения.
На первом этапе для локализации корней
используется теорема: «Если функция
![]() ,
определяющая уравнение
,
определяющая уравнение
![]() ,
непрерывна и на концах отрезка
,
непрерывна и на концах отрезка
![]() принимает значения разных знаков, т.е.
принимает значения разных знаков, т.е.
![]() ,
то на этом отрезке содержится хотя бы
один корень этого уравнения». Основной
задачей на данном этапе является
максимальное уменьшение интервала
локализации, чтобы уменьшить число
корней на этом интервале. В вычислительной
практике обычно используют следующие
способы локализации корней:
,
то на этом отрезке содержится хотя бы
один корень этого уравнения». Основной
задачей на данном этапе является
максимальное уменьшение интервала
локализации, чтобы уменьшить число
корней на этом интервале. В вычислительной
практике обычно используют следующие
способы локализации корней:
а) средствами машинной графики функция
![]() представляется на дисплее, и приближенно
определяются отрезки, которым принадлежат
точки
представляется на дисплее, и приближенно
определяются отрезки, которым принадлежат
точки
![]() ;
;
б) средствами математического анализа
исследуется функция
![]() и строится ее график. Пример такого
графика приведен ниже на рисунке 1.
и строится ее график. Пример такого
графика приведен ниже на рисунке 1.
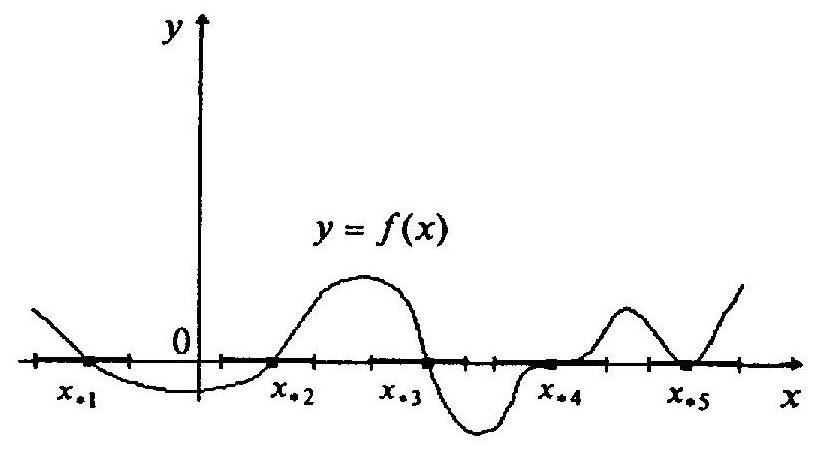
Рисунок 1 – График функции
![]()
На втором этапе для вычисления корней
уравнения используются различные методы
приближенных вычислений с заданной
точностью. В основном используются
различные итерационные методы, позволяющие
построить последовательность значения
аргумента
![]() ,
,
![]() по условию:
по условию:
![]() ,
(2)
,
(2)
где
![]() - точное значение корня;
- точное значение корня;
![]() - заданная точность вычислений
- заданная точность вычислений
Ниже рассмотрим основные эти методы вычислений.
1.2. Метод половинного деления (метод бисекции)
Пусть дано уравнение
![]() и отделен простой корень
и отделен простой корень
![]() ,
т.е. найден такой отрезок
,
т.е. найден такой отрезок
![]() ,
что
,
что
![]() принадлежит этому отрезку и на концах
этого отрезка функция принимает значения,
противоположные по знаку (
принадлежит этому отрезку и на концах
этого отрезка функция принимает значения,
противоположные по знаку (![]() ).
Отрезок
).
Отрезок
![]() называется начальным интервалом
неопределенности, потому что известно,
что корень ему принадлежит, но его
местоположение с требуемой точностью
не определено.
называется начальным интервалом
неопределенности, потому что известно,
что корень ему принадлежит, но его
местоположение с требуемой точностью
не определено.
Процедура уточнения положения корня
заключается в построении последовательности
вложенных друг в друга отрезков, каждый
из которых содержит корень уравнения.
Для этого находится середина текущего
интервала неопределенности
![]()
![]() ,
и в качестве следующего интервала
неопределенности из двух возможных
выбирается тот, на концах которого
функция
,
и в качестве следующего интервала
неопределенности из двух возможных
выбирается тот, на концах которого
функция
![]() имеет разные знаки. Иллюстрация данного
метода приведена на рисунке 2.
имеет разные знаки. Иллюстрация данного
метода приведена на рисунке 2.
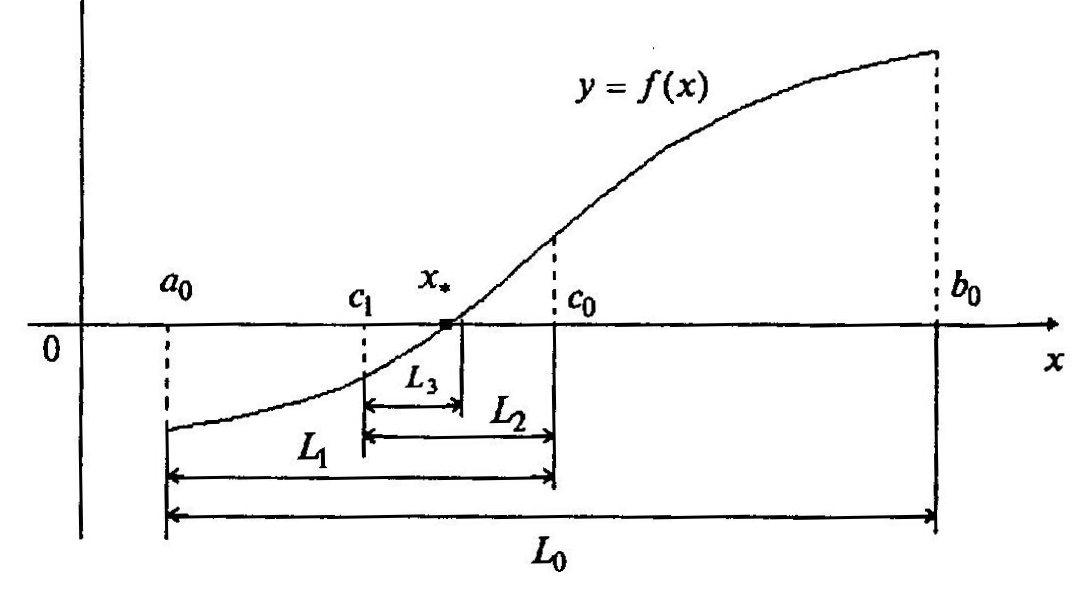
Рисунок 2 – Графическая интерпретация нахождения корней
функции
![]() методом бисекции
методом бисекции
Процесс вычислений завершается, когда
длина текущего интервала неопределенности
становится меньше заданной величины
![]() ,
задающей точность нахождения корня. В
качестве приближенного значения корня
берется середина последнего интервала
неопределенности.
,
задающей точность нахождения корня. В
качестве приближенного значения корня
берется середина последнего интервала
неопределенности.
Достоинство данного метода – он позволяет
найти простой корень уравнения для
любых непрерывных функций
![]() при любых значениях
при любых значениях
![]() ,
таких, что
,
таких, что
![]() .
.
Недостатки данного метода – 1) схождение к точному решению происходит медленно; 2) данный метод не обобщается на системы нелинейных уравнений и не может быть использоваться для нахождения корней четной кратности.
1.3. Метод хорд
Данный метод при одних и тех же начальных
условиях обеспечивает более быстрое
нахождение корня, чем метод бисекции.
При использовании метода хорд отрезок
![]() делится не пополам, а в отношении
делится не пополам, а в отношении
![]() .
.
Геометрически метод хорд эквивалентен
замене кривой
![]() хордой, проходящей через точки
хордой, проходящей через точки
![]() и
и
![]() ,
что иллюстрирует рисунок 3.
,
что иллюстрирует рисунок 3.
Уравнение хорды AB имеет следующий вид:
![]() .
(3)
.
(3)
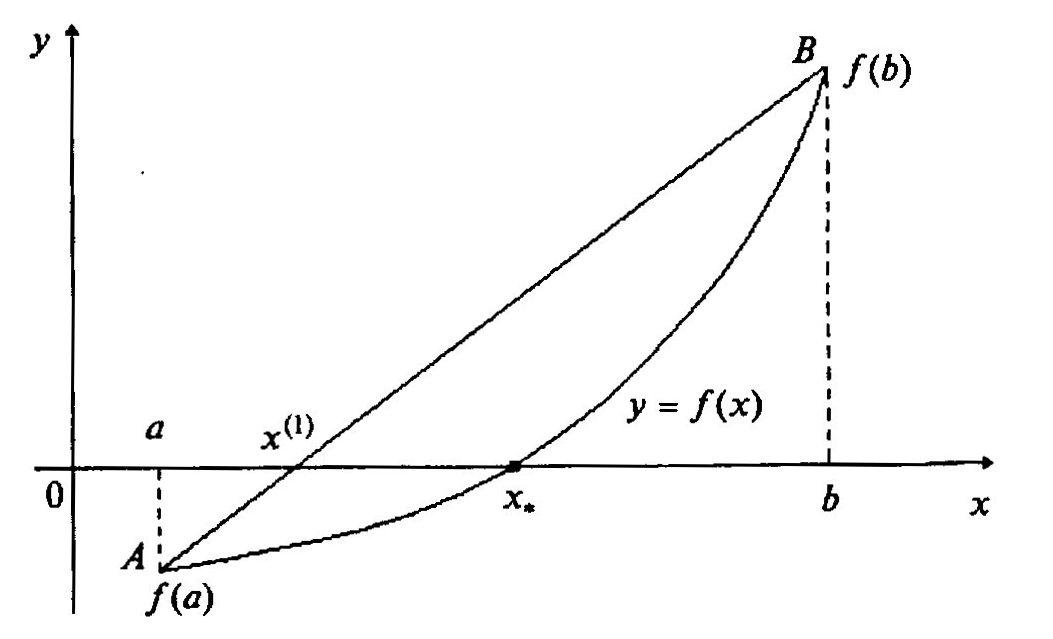
Рисунок 3 – Графическая интерпретация нахождения корней
функции
![]() методом хорд
методом хорд
Для точки пересечения хорды с осью
абсцисс имеем
![]() и
и
![]() ,
тогда из уравнения (3) получим
,
тогда из уравнения (3) получим
![]() (4)
(4)
Затем находится значение функции
![]() .
Если
.
Если
![]() ,
то в точку
,
то в точку
![]() переносим правую границу интервала, а
конец хорды в точке
переносим правую границу интервала, а
конец хорды в точке
![]() остается неподвижным. Этому случаю
соответствуют формулы
остается неподвижным. Этому случаю
соответствуют формулы
![]() ;
(5)
;
(5)
![]()
![]() .
(6)
.
(6)
Данный случай иллюстрирует рисунок
4,а. Если же
![]() ,
то в точку
,
то в точку
![]() переносим левую границу интервала, а
конец хорды в точке
переносим левую границу интервала, а
конец хорды в точке
![]() остается неподвижным. Этому случаю
соответствуют формулы
остается неподвижным. Этому случаю
соответствуют формулы
![]() ;
(7)
;
(7)
![]()
![]() .
(8)
.
(8)
Данный случай иллюстрирует рисунок 4,б.
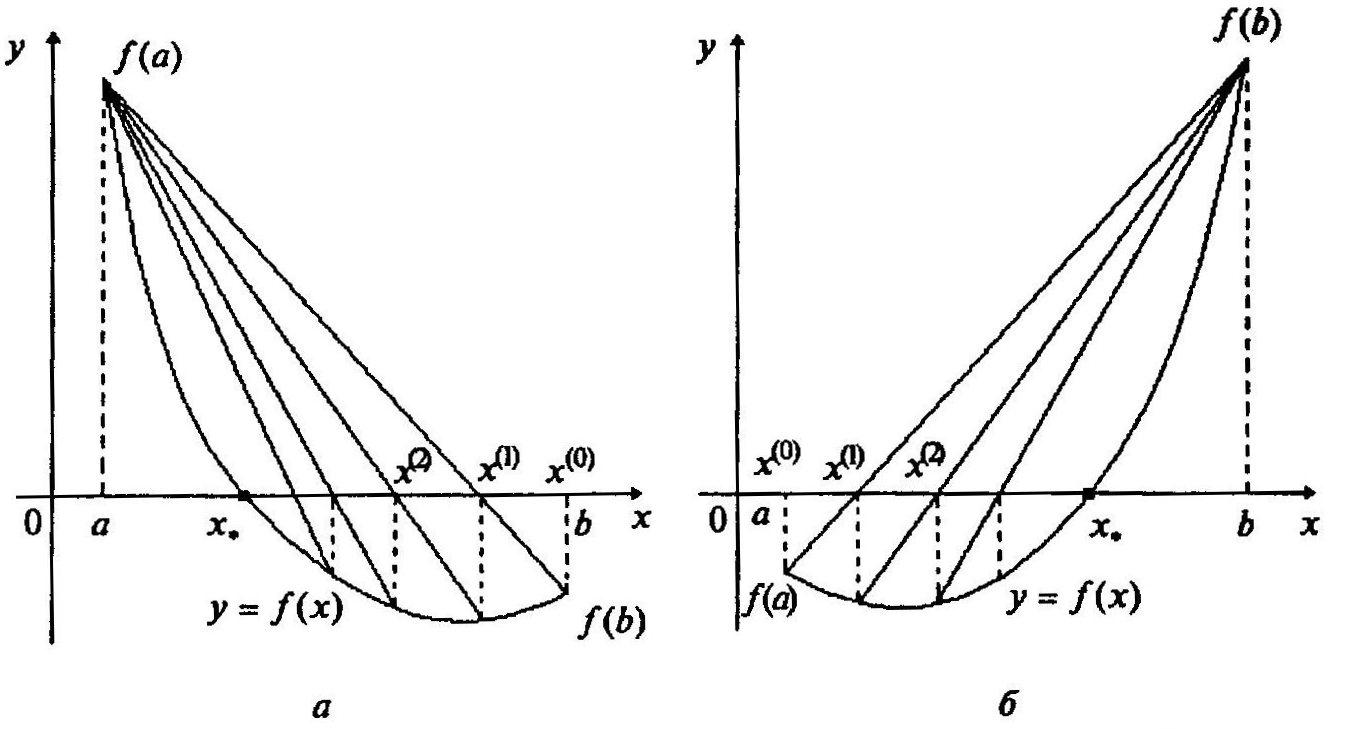
Рисунок 4 – Выбор неподвижного конца
хорды функции
![]()
Расчеты прекращаются, когда выполняется
условие
![]() .
В качестве решения принимается значение
.
В качестве решения принимается значение
![]() .
.
Достоинство метода – сходимость метода хорд линейная, но более быстрая, чем сходимость метода бисекции.
Недостаток метода – необходимо определять неподвижный конец хорды.
1.4. Метод Ньютона (метод касательных)
Метод Ньютона является одним из наиболее
популярных численных методов. Он быстро
сходится, так как имеет квадратичную
сходимость, и имеет различные модификации.
Однако этот метод эффективен при весьма
жестких ограничениях на функцию
![]() :
:
а) существование второй производной
функции
![]() на интервале
на интервале
![]() ;
;
б) удовлетворение первой производной
условию
![]() для всех значений
для всех значений
![]() на данном интервале;
на данном интервале;
в) знакопостоянство
![]() и
и
![]() для всех значений
для всех значений
![]() на данном интервале.
на данном интервале.
Поэтому данный метод целесообразно использовать совместно с другими методами, например, с методом бисекции.
Геометрическая интерпретация метода Ньютона приведена на рисунке 5 и состоит в следующем.
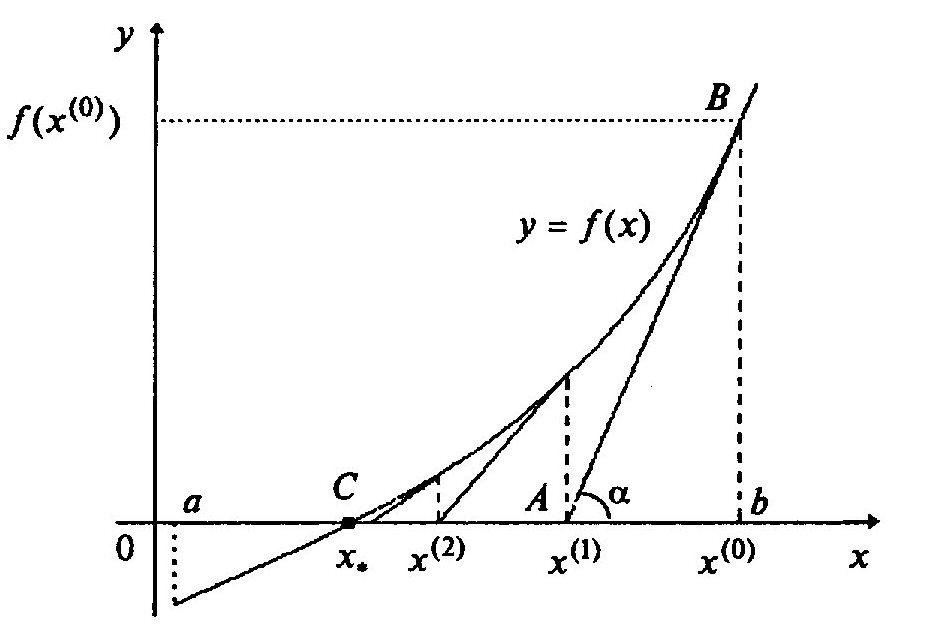
Рисунок 5 – Графическая интерпретация нахождения корней
функции
![]() методом Ньютона
методом Ньютона
Задается начальное приближение
![]() .
Для сходимости решения необходимо
выполнение в данной точке условия
.
Для сходимости решения необходимо
выполнение в данной точке условия
![]() (9)
(9)
Далее строится касательная к кривой
![]() в точке
в точке
![]() ,
т.е. кривая заменяется прямой линией. В
качестве следующего приближения
выбирается точка пересечения этой
касательной с осью абсцисс. Процесс
построения касательных и нахождения
точек пересечения с осью абсцисс
повторяется до тех пор, пока приращение
аргумента не станет меньше заданной
величины
,
т.е. кривая заменяется прямой линией. В
качестве следующего приближения
выбирается точка пересечения этой
касательной с осью абсцисс. Процесс
построения касательных и нахождения
точек пересечения с осью абсцисс
повторяется до тех пор, пока приращение
аргумента не станет меньше заданной
величины
![]() .
.
Выведем расчетную формулу метода
Ньютона. Вместо участка кривой ВС (точка
С соответствует
![]() )
возьмем участок АВ – касательную,
проведенную в точке (
)
возьмем участок АВ – касательную,
проведенную в точке (![]() ,
,
![]() ).
Для этого отрезка справедливо конечное
соотношение
).
Для этого отрезка справедливо конечное
соотношение
![]() ,
(10)
,
(10)
где
![]() - угол наклона касательной в точке (
- угол наклона касательной в точке (![]() ,
,
![]() ).
Решая соотношение (10) относительно
).
Решая соотношение (10) относительно
![]() ,
получим
,
получим
![]() .
(11)
.
(11)
В общем виде выражение (11) будет иметь вид
![]() .
(12)
.
(12)
Достоинства метода – это один из самых быстро сходящихся методов. Там, где при использовании метода бисекции выполняется 20 итерации, методом Ньютона достаточно выполнить 2 – 3 итерации.
Недостатки метода – жесткие требования к функции, перечисленные выше. Кроме того, необходимо вычисление не только функции, но и ее производной, что увеличивает трудоемкость расчетов.
1.5. Модификации метода Ньютона
1.5.1. Упрощенный метод Ньютона
При использовании данного метода вместо формулы (12) используется следующая формула
![]() .
(13)
.
(13)
При использовании данного метода производная подсчитывается только в точке начального приближения, а на последующих итерациях не учитывается. Первая итерация совпадает с первой итерацией метода Ньютона. На последующих итерациях соответствующие отрезки параллельны касательной, проведенной в начальной точке. Для данной модификации снимаются некоторые ограничения метода касательных, например, условие знакопостоянства производных. Сходимость упрощенного метода Ньютона линейная.
1.5.2. Метод секущих.
В этой модификации метода Ньютона
производная
![]() заменяется отношением конечных приращений
заменяется отношением конечных приращений
![]() .
(14)
.
(14)
Тогда формула (12) примет вид
![]() .
(15)
.
(15)
Достоинства данных модификаций – снижение трудоемкости расчетов. Снижение некоторых ограничений на функцию.
Недостаток – снижение скорости сходимости почти в два раза.
1.6. Метод простой итерации
При использовании данного метода
уравнение вида
![]() путем преобразований следует привести
к виду
путем преобразований следует привести
к виду
![]() .
Для обеспечения сходимости необходимо
найти значение производной функции
.
Для обеспечения сходимости необходимо
найти значение производной функции
![]() в области искомого корня. Если
в области искомого корня. Если
![]() ,
то сходимость решения будет обеспечена,
если же
,
то сходимость решения будет обеспечена,
если же
![]() ,
то процесс вычислений будет расходящийся.
Если функция
,
то процесс вычислений будет расходящийся.
Если функция
![]() может быть найдена несколькими способами,
то обычно для одного из них метод
сходится.
может быть найдена несколькими способами,
то обычно для одного из них метод
сходится.
Сначала задается начальное значение
![]() и вычисляется функция
и вычисляется функция
![]()
![]() (16)
(16)
В общем случае
![]() (17)
(17)
Геометрически данная задача сводится
к нахождению абсциссы точки пересечения
прямой
![]() и кривой
и кривой
![]()
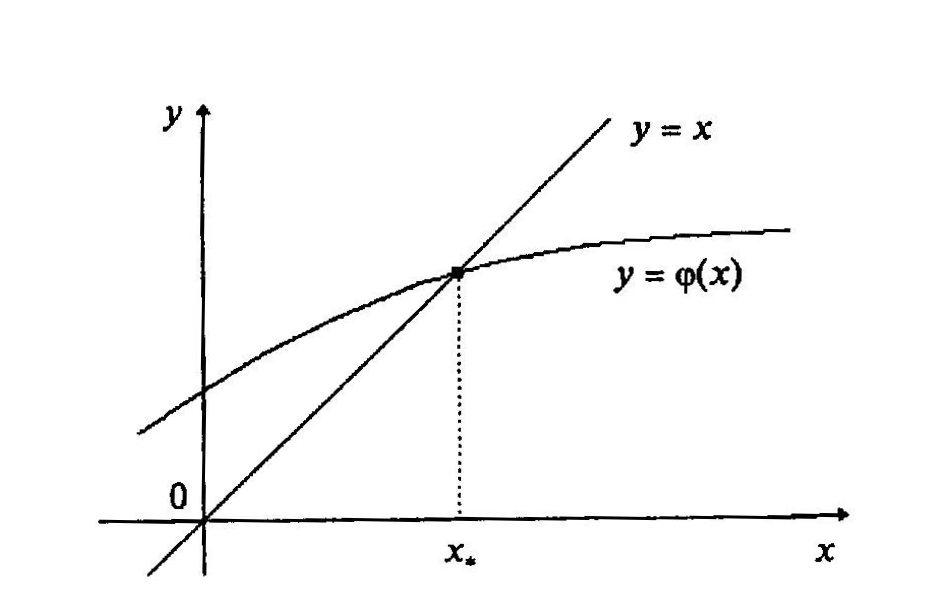
Рисунок 6 – Графическая интерпретация нахождения корней
функции
![]() методом простой итерации
методом простой итерации
Расчеты прекращаются, если выполняется условие
![]() .
(18)
.
(18)
В качестве решения принимается значение
![]() .
.
