Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

leading to a splitting into two electronic states of A and B symmetry (in C2v). For a given geometry, one of the states, say the A state, is the ground state and the other, an excited state. However, for a different geometry, their relative energy must switch, as we have seen for the H3 and H4 systems. We shall find that this is the case for other Jahn–Teller systems. In particular, if the minima transform as an A-type representation, the TS transform as B-type.

There is an odd number of equivalent spin-paired structures around the degeneracy: for a D3h case, three, for D5h case, five, and so on. These structures occupy separate minima around the conical intersection, or are located around an isoenergetic moat in the Mexican hat. The transition between them requires a change in the spin pairing, which, by the Longuet-Higgins rule, must be phase inverting. This means that the symmetry of electronic wave function at the transition state is in general different than that of the minima. Thus, the electronic wave function of different nuclear geometries on the ground-state surface may transform according to different symmetry species.

A.An Example: The Cyclopentadienyl Radical

and Cation Systems

The cyclopentadienyl radical and the cyclopentadienyl cation are two wellknown Jahn–Teller problems: The traditional Jahn–Teller treatment starts at the D5h symmetry, and looks for the normal modes that reduce the symmetry by firstor second-order vibronic coupling. A Longuet-Higgins treatment will search for anchors that may be used to form the proper loop. The coordinates relevant to this approach are reaction coordinates.

1.Cyclopentadienyl Radical (CPDR)

This system was analyzed using ab initio (MO–CI) methods [72,73]. In the cyclopentadienyl radical, three electrons occupy a pair of e001 p MOs that are degenerate in D5h symmetry. This gives rise to a degenerate 2E100 state, which by the Jahn–Teller theorem should distort away from D5h symmetry along a degenerate e02-type vibration. The resulting states are of A2 and B1 symmetry. Five equivalent minima of C2v symmetry are obtained, which may be connected by a motion that does not pass through the central D5h-symmetric structure. It turns out [73,74] that the barriers between the five equivalent structures are small, so that the system can pseudorotate among them—a typical Mexican hat case.

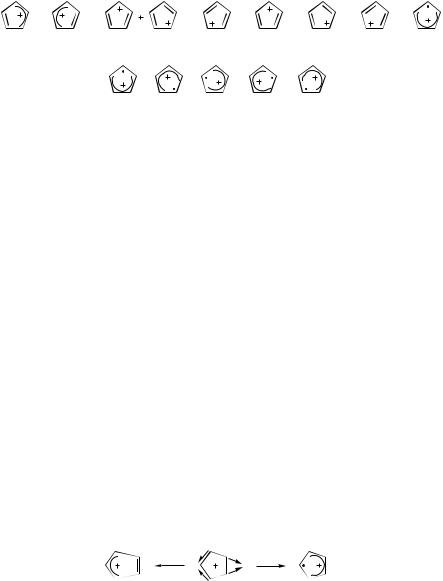
A simple VB approach was used in [75] to describe the five structures. Only the lowest energy spin-pairing structures I (B1 symmetry) of the type {12,34,5} were used (Fig. 21). We consider them as reactant–product pairs and note that the transformation of one structure (e.g., Ia) to another (e.g., Ib) is a threeelectron phase-inverting reaction, with a type-II transition state. As shown in Figure 22, a type-II structure is constructed by an out-of-phase combination of

Figure 21. The five equivalent spin-paired structures of CPDR.

the two type-I structures. The degenerate 2E100 state is the lowest state of D5h symmetry: It lies on the ground-state surface and is constructed from a combination of the five. Type-II are A2 symmetry structures, and they turn out to be isoenergetic with type-I. Their relatively strong stabilization is due to the allyl-type resonance. Their description as transition states is thus a matter of choice—type-I structures could be considered as transition states between two type-II structures.

The electronic spectrum of the radical has been recorded long before a satisfactory theoretical explanation could be provided. It was realized early on that the system should be Jahn–Teller distorted from the perfect pentagon symmetry (D5h point group). Recently, an extensive experimental study of the high-resolution UV spectrum was reported [76], and analyzed using Jahn–Teller formalism [73].

It was shown by several workers that in this case the first-order Jahn–Teller distortion is due to an e02 vibration, and that the second-order distortion vanishes. Therefore, in terms of simple Jahn–Teller theory, the ‘‘moat’’ around the symmetric point should be a Mexican hat type, without secondary minima. This expectation was borne out by high-level quantum chemical calculations, which showed that the energy difference between the two expected C2v structures (2A2 and 2B1) were indeed very small [73].

The system provides an opportunity to test our method for finding the conical intersection and the stabilized ground-state structures that are formed by the distortion. Recall that we focus on the distinction between spin-paired structures, rather than true minima. A natural choice for anchors are the two C2v structures having A2 and B1 symmetry shown in Figures 21 and 22: In principle, each set can serve as the anchors. The reaction converting one type-I structure to another is phase inverting, since it transforms one allyl structure to another (Fig. 12).

{12,34,5} {12,3,45}

55

Type-II structures are formally the out-of-phase transition states between two type-I structures, even if there is no measurable barrier.

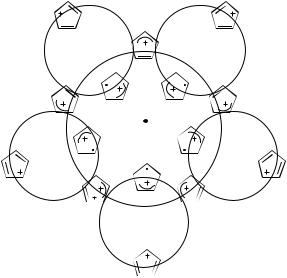
The complete loop is shown in Figure 23: It has five phase-inverting reactions, and therefore is a phase-inverting loop. The degeneracy that lies within the loop is the symmetric D5h structure—at this symmetry all five type-I structures are degenerate. Alternatively, the five B1 structures could serve as anchors, the transitions between any pair are also phase inverting, with the A2 structures functioning as transition states. This example emphasizes the cardinal importance of spin pairing as the basis for choosing anchors—the conventional choice is a nuclear structure that lies in an energy minimum, but this is not an essential requirement.

This example may be used to address another issue concerning LonguetHiggins loops: What is the minimum number of anchors needed to form a loop. Formally, one might choose three anchors (e.g., Ia, Ic, and Id), and use them as a loop. Inspection of Figure 23 shows that the conical intersection is formally encircled by a loop connecting these structures. It is also easily verified that the loop is an ip2 phase inverting one: The Ic ! Id reaction is phase inverting, and the Ia ! Ic and the Ia ! Id reactions are phase preserving. However, one of the conditions for a proper loop was that all reactions must be elementary, that is, there must not be an intermediate between any two anchors. This condition is not satisfied for the transformation Ia ! Ic (or Ia ! Id): motion along this trajectory leads up-hill (on the slope of the cone leading to the E100 degeneracy). Somewhere on the way, the minimum energy path will lead the system to Ib, which is therefore an intermediate. Thus, the smallest loop must pass through all five type-I structures.

Other spin-pairing forms that may in principle be used to construct a loop are shown in Figure 24.

Structures III and IV that have different spin-pairing schemes are expected to be higher in energy than type-I because of the strain introduced by the cyclopropyl rings. They may be anchors for secondary conical intersections around the most symmetric one.

2.Cyclopentadienyl Cation (CPDC)

In the case of the cyclopentadienyl cation, there are only two electrons in the e001 p molecular orbitals that are degenerate in D5h symmetry. The MO treatments [72,77] predict three low-lying electronic states: 3A02 (which is the ground state), 1A01, and a degenerate 1E20 state. As in the case of the radical, an e0-type vibrational mode is expected to lower the symmetry of the system and produce a lower energy singlet state. In this case, the E state splits to states of A1 and B2 symmetry. This system is thus analogous to the cyclopentadienyl radical one— five equivalent C2v structures are expected to be formed upon distortion of the D5h one. These structures are situated around the degeneracy in a Mexican hat arrangement. The MO calculations found two very close lying 1A1 structures [72,77]. The B1 state, expected from the Jahn–Teller treatment, was not discussed by [72].

Figure 25 shows the results of the C2v distortion induced by a degenerate e02 vibration that removes the D5h degeneracy (compare Fig. 23). By symmetry, five

Figure 28. Top: Construction of type-VII structure of B2 symmetry. Bottom: the five type-VII structures.

type-VII. It may be conceived as a three-electron combination spread over four carbon atoms. A single electron resides on the fifth carbon atom.

Types-VI and -VII structures can be formed from the symmetric D5h structure by the e02 vibration as shown in Figure 29, in accord with the Jahn– Teller theorem.

The B2 form of the cyclopentadienyl cation was not studied extensively. In [77], it was referred to as an electronically excited state. According to the Jahn–Teller theorem, at a certain geometry it should be part of the ground state, formed by the distortion of the degenerate structure. This requirement is fulfilled, of course, if it is indeed a TS between two ground-state species. We computationally verified this proposition as follows. The exact structure of the system at the degeneracy point was searched for under D5h symmetry constraint. The C–C bond distance rC C for the symmetric D5h cation at the conical

intersection was found by calculating the energy of the two states point by point

¼ ˚ with different rC C values. A minimum energy was obtained at rC C 1:437 A.

At this point, the D5h symmetry was removed, and a search for an electronic state of B2 symmetry was conducted. A structure with the geometry shown in Figure 30 was found. At this geometry, the B2 state is lower in energy than any other, and therefore lies on the ground-state surface. Going either way to the type-VI structure, still on the ground-state surface, the energy decreased—the

Figure 29. The effect of the phase-preserving component of the degenerate e02 distorting mode. It may be regarded as a major component of the reaction coordinate that leads to the A1 structure (going left, one phase of the mode). Going right, the other phase of the same vibration, the B2 state is formed. (A type-V structure is also obtained along the same coordinate).

Va

main conical intersection

S secondary conical intersection

Figure 32. The main symmetric conical intersection of cyclopentadienyl cation, and five secondary conical intersections around it.

the geometry of the B2 transition state, the A1 state is of higher energy, and thus an excited states, even if by a small margin.

The case of CPDC can be used to address the issue of the loop’s size and the number of conical intersections near a Jahn–Teller degeneracy. If we carry the system around a loop encircling all six degeneracies, the total electronic wave function will not change sign, and the phase-change theorem will appear to be violated. This point, relating to the ‘‘radius’’ of the loop, was raised by several authors [11,78]. Zwanziger and Grant [78] showed that in the case of the 22E0 state of Na3, three degeneracies are found nearby the main Jahn–Teller one. They analyzed the system using linear and quadratic coupling terms. Our discussion of the cyclopentadienyl radical shows how a problem of this nature is treated by the spin-pairing model. The extra five satellite conical intersections of CPDR arise from the fact that there are more spin-paired functions surrounding the main degeneracy point. In the case of the first degeneracies of the H3 and Na3 systems, the lowest 2E0 state (12E0) displays a single degeneracy. The Zwanziger–Grant effect arises in the second 2E0 state, since other spin

pairing structure with similar energies are possible on the excited-state surface, for example, such that involve 3p electrons. Due to symmetry, only three such structures are possible, giving rise to three secondary loops, in analogy with the five loops shown in Figure 32.

VI. EXAMPLES

In this section, we apply the phase-change rule and the loop method to some representative photochemical systems. The discussion is illustrative, no comprehensive coverage is intended. It is hoped that the examples are sufficient to help others in applying the method to other systems. This section is divided into two parts: in the first, loops are constructed and a qualitative discussion of the photochemical consequences is presented. In the second, the method is used for an in-depth, quantitative analysis of one system—photolysis of 1,4- cyclohexadiene.

A.Loops in Molecular Photochemistry: Qualitative Discussion

Some prototype systems were presented in Sections I–IV; here, we offer a more extended discussion and application to realistic photochemical systems.

1.Four-Electron Problems

The prototype system for all four electron problem is the H4 system, discussed in Section II.

Ethylene. A possible loop for ethylene photolysis was presented in Figure 14. Experimentally, irradiation into the first absorption band [populating the B(11B1u) state] leads to cis–trans isomerization as well as to a H atom shift. The covalent A state lies at a very high energy in the planar form [79,80], but is the lowest excited singlet in the perpendicular one. This system was studied as early as 1985 by Ohmine [6], who reported a conical intersection that involves pyramidalization, and may lead to hydrogen-atom transfer. He calculated the conical intersection to be found along two coordinates—a phase inverting one (rotation around the double bond) and a phase preserving one, forming a methyl carbene (hydrogen-atom transfer) or a charge separated intermediate. Similar results were obtained more recently by the extensive studies of Ben-Nun and Martinez ([10] and references cited therein). Figure 33 shows a phase-inverting loop for the cis–trans isomerization, that leads also to a hydrogen-atom shift. The third anchor in this loop may appear as a carbene (CH3CH:) or as a zwitterion (CH2 CHþ2 ), see Figure 1(4). The conical intersection encircled by the loop is termed CIH, for hydrogen-atom transfer.