2.8. Цепь переменного тока с катушкой индуктивности

Под действием напряжения u по катушке протекает ток i = I_msinωt (рис. 2.12). Приложенное напряжение u является суммой двух составляющих – активной u _R и реактивной (индуктивной) u_L :

u = u _R + u _L = U_msinωt + U_msin (ωt + 90º).

Рис. 2.12. Цепь переменного тока с активно-индуктивной нагрузкой

Активная составляющая u_R = i·R совпадает по фазе с током, а индуктивная u _L = i·X_L опережает по фазе ток на четверть периода.

Векторную диаграмму для этой цепи обычно начинают строить с вектора тока Ī так как при последовательном соединении элементов ток на всех участках цепи одинаков (рис. 2.13, а). Далее откладываем вектор Ū_R который совпадает по фазе с вектором тока Ī. Под углом 90° к вектору Ī откладываем вектор напряжения Ū_L. Результирующий вектор Ū = Ū_R + Ū_L. Из треугольника напряжений определяем действующее значение приложенного напряжения:

.

Треугольнику напряжений подобен треугольник сопротивлений (рис.2.13, б), где – полное сопротивление цепи. Из треугольника сопротивлений получаем следующие расчетные формулы:

; ;.

Ток в цепи определяется по закону Ома: .

Рис. 2.13. Векторная диаграмма цепи с последовательным соединением R, L (а);

треугольник сопротивлений (б)

2.9. Цепь переменного тока с конденсатором

Если по цепи (рис. 2.14) протекает ток i = I_msinωt, то подводимое напряжение u равно сумме напряжений на активном сопротивлении и конденсаторе:

u = u_R + u_C = U_msinωt + U_msin(ωt – 90º).

Рис. 2.14. Цепь переменного тока с активно-емкостной нагрузкой

Активная составляющая напряжения совпадает по фазе с током, а емкостная составляющая отстает на четверть периода. Действующее значение подводимого к цепи напряжения

.

Векторная диаграмма строится аналогично предыдущему случаю (рис. 2.15). За исходный вектор принимаем вектор тока Ī. Вектор Ū_R совпадает по фазе с вектором Ī. Под углом 90° откладываем вектор Ū_C. Вектор приложенного напряжения к цепи Ū = Ū_R + Ū_с.

а б

Рис. 2.15. Векторная диаграмма цепи с последовательным

соединением R, C (а); треугольник сопротивлений (б)

2.10. Комплексный метод расчета цепей переменного тока

Тригонометрическая форма расчета электрических цепей практически применима только для простейших цепей, не содержащих большого числа контуров и источников, поэтому широкое применение получил алгебраический метод, позволяющий рассчитывать цепи переменного тока аналогично цепям постоянного тока – комплексный метод (метод комплексных амплитуд, или символический метод).

Комплексное число, соответствующее точке, в которой лежит конец вектора (рис. 2.16), может быть записано в следующих формах: алгебраической = a₁ + ja₂; тригонометрической = a(cosα + jsinα); показательной = a·e^jα и полярной (угловой) = a·∟α_,

где: a₁ = a·cosα = Re[] – действительная (вещественная) часть комплексного числа ;

a₂ = a·sinα = Im[] – мнимая часть комплексного числа ;

–мнимая единица, или оператор поворота на угол

Рис. 2.16. Изображение вектора на комплексной плоскости

π/2 = 90° (умножение на j сводится к повороту вектора против часовой стрелки на угол π/2, а умножение на к повороту вектора на прямой угол по часовой стрелке);

–модуль комплексного числа (всегда положителен);

–угол или аргумент комплексного числа.

Показательная форма записи комплексного числа получается из формулы Эйлера:

cosα ± j·sinα = e^±jα

Комплексное число =a₁ – ja₂ = ae^-jα называется комплексно-сопряженным числу =a₁ + ja₂ = ae^jα . Произведение компексно-сопряженных чисел – число действительное, равное квадрату их модуля:

.

Умножение комплексного числа ae^jα на число е^jφ сводится к повороту вектора а в комплексной плоскости на угол α + φ:

ae^jα · e^jφ = ae^j(α+φ).

Сложение и вычитание комплексных чисел производится в алгебраической форме:

+ = (a₁ + ja₂) ± (b₁+ jb₂) = (a₁±b₁) + j(a₂±b₂).

Умножение и деление комплексных чисел может производиться в алгебраической и показательной формах:

· = (a₁ + ja₂)· (b₁+ jb₂) = (a₁b₁ – a₂b₂) + j (a₂b₁ + a₁b₂) = ae^jα · be^jβ = abe^j(α+β) .

.

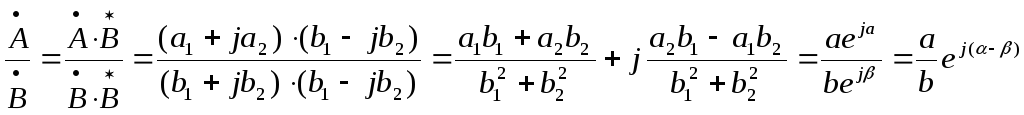Возведение в степень производится следующим образом:

(ae^jα)ⁿ = aⁿe^jαn = aⁿ (cosαn + jsinαn).

Рассмотрим проекции вращающегося против часовой стрелки с постоянной угловой скоростью ω вектора (рис. 2.17). Проекция на действительную ось – I_m cosα. Проекция на мнимую ось – jI_m sinα.

Рис. 2.17. Проекции вращающегося вектора на комплексную плоскость

Тогда согласно формуле Эйлера

I_m e^jα = I_m cosα + jI_m sinα.

Угол α может быть любым. Если α = ωt + ψ, где ψ – начальная фаза, то

I_m e^j(ωt+ψ) = I_m cos (ωt + ψ) + jI_m sin (ωt + ψ),

где: I_m cos (ωt + ψ) – действительная часть комплексного числа;

jI_m sin (ωt + ψ) – мнимая часть комплексного числа.

Для единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для момента времени ωt _{= 0}. Для этого момента времени вектор I_m e^j(ωt+ψ) будет равен I_m e^jψ = , где – комплексная амплитуда тока, модуль ее равен 1_т, а угол α на комплексной плоскости равен начальной фазе ψ _. Аналогично можно записать для э.д.с. и напряжения:

Например, если ток, протекающий по цепи, равен i = 12sin (ωt + 30°)А, то в данном случае I_m = 12 А, ψ = 30º , следовательно, комплексная амплитуда тока = 12e^j30º , а комплекс тока (комплексный ток)