Мальханов - Общая Физика

tg α = (a1Sinα1 + Sinα2)/(a1 Cosα1 + a2Cosα2)

§ 7 Сложение взаимно перпендикулярных колебаний

Одна и та же точка совершает периодические колебания в двух взаимно перпендикулярных направлениях. Это происходит одновременно. Имеем параметрический вид (через t) записи уравнений

Y

OX

Здесь дан параметрический вид (через переменный параметр t) уравнения траектории точки. Точка в плоскости x

- y совершает какое-то движение. Найдем форму траектории y(x) исключив t. Имеем

100

x = a Cos (ω0t), y = b Cos (ω0t + ϕ)

Cos (ω0t) = x/a 1 - Sin2(ω0t) = (x/a)2

y/b = Cos (ω0t + ϕ) = Cos(ω0t)Cosϕ - Sin(ω0t)Sinϕ = [(x/a) Cosϕ] - [1 - (x/a)2]1/2Sinϕ

[1 - (x/a)2]Sin2ϕ = (x/a)2Cos2ϕ - 2xyCosϕ/ab - (y/b)2

Sin2ϕ = (x/a)2 + (y/b)2 – (2xy/ab) Cosϕ (**)

Проанализируем полученное выражение (**)

1.ϕ = 0 (x/a - y/b)2 = 0 x/a = y/b y = bx/a - прямая

2.ϕ = ±π (x/a + y/b)2 = 0 y = - bx/a - прямая

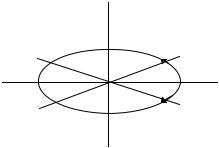
3.ϕ = ±π/2 (x/a)2 + (y/b)2 = 1 – эллипс

экспериментально осциллографически можно находить отношение частот колебаний. Направление колебаний определяется по возрастанию или убыванию косинуса.

x = a Cos (ω0t + α), y = b Cos (ω0t + β)

§ 8 Биения

Пусть имеем два колебания одного направления с одинаковыми амплитудами, но незначительно отличающимися частотами (например, на 10%), тогда

ω1 = ω, ω2 = ω + ∆ω, x1 = a Cos(ωt), x2 = a Cos(ω + ∆ω)t

x = x1 + x2 = = a[Cos(ωt) + Cos(ω + ∆ω)t] =

=a 2 Cos{[ωt + (ω + ∆ω)t]/2} Cos{[ωt - (ω + ∆ω)t]/2} =

=2aCos(ωt + ∆ωt/2) Cos(∆ωt/2)= (∆ω << ω, ω/∆ω≈ 10раз) =

=2a Сos(ωt)Cos(∆ωt/2).

Если построить график такой функции, то роль меняющейся амплитуды может быть приписана А = |2а Cos(∆ωt/2)| . Заметим, что плавно меняющаяся функция будет искажена в меру отличия частот. Периодами двух периодических функций

являются соответственно: высокочастотной - Т = 2π/ω, низкочастотной -

ТА = 2π /∆ω

График представлен для ω = 100 Гц, ∆ω = 10 Гц, А = 1, при этом Т 62,8 мс, ТА

0,63 с.

102

§9 Ангармонический осциллятор Пусть

U (x) = (kx2/2) - skx3/3

Здесь оставлены члены ряда по четвертый включительно

U (x) = U (0) + U′(0)x + U′′(0)x2/2! + U ′′′(0)x3/3! + ...

U (0) = 0 (выбором начала отсчета), U′ (0) = F (0) = 0,

U ′′(0) = k, U′′′(0) = -2sk U (x) ≈ (kx2/2) - skx3/3

103

F (x) = - dU(x)/dx = - kx + skx2 md2x/dt2 = -kx + skx2 d2x/dt2 + ω02x - sω02 x2 =0. (*) (d2x/dt2 + ω02x = sω02 x2)

Наличие члена х2 делает это уравнение нелинейным. Его решение будем искать в виде

x = a (Cosωt + qCos2ωt) + x1 = a Cosωt + aqCos2ωt + x1 . (1)

Здесь q и х1 - два неизвестных параметра (для уравнения второго порядка). Для их определения подставим решение (1) в исходное уравнение (*) d2x/dt2 + ω02x - sω02 x2 =0. Вычислим вторую производную и квадрат неизвестного.

x2 = (a Cos(ωt) + a q Cos(2ωt) + x1)2 = a2Cos2 (ωt) + a2q2Cos2 (2ωt) + x12 +

+ (по парные удвоенные произведения).

Считаем q1 и x1 малыми и пренебрежем всеми членами, сомножителями которых они являются.

x2 ≈ a2Cos2ωt = (a2/2)(1 + Cos2ωt) = (a2/2) + (a2Cos2ωt)/2 (3)

Подставим (1, 2 и 3) в исходное уравнение (*) d2x/dt2 + ω02x - sω02 x2 =0, имеем

-aω2Cos (ωt) - 4aqω2Cos (2ωt) + aω0 2 Cosωt + ω02aqCos(2ωt) + ω02x1 - sω02a2/2 –

-(sω02a2 /2) Cos (2ωt) =

= (ω02a - aω2)Cos(ωt) + (ω02aq - sω02a2/2 - 4aqω2)Cos(2ωt)+ ω02x1 - sω02a2/2 = 0

Для равенства нулю последнего выражения необходимо равенство нулю всех его слагаемых

1. ω = ω0 a(ω02 - ω2)Cos(ωt) = 0

104

2.ω02aq - sω02a2/2 - 4aqω02 = 0 (ω0 ≠ 0) 3q = as/2 a = 6q/s

3.ω02x1 - aω02a2/2 = 0 x1 = sa2 /2.

Найдем среднее значение от смещения x

< х > = < a(Cosωt + qCos2ωt) + x1> =

(так как средние значения от периодических функций равны нулю)

<x> = x1, но x1 = sa2/2 x = sa2/2.

Применим полученный результат к цепочке атомов в твердом теле. С одной стороны полная энергия гармонического осциллятора E пропорциональна квадрату амплитуды (E ~ a2). Смещение также пропорционально квадрату амплитуды согласно нашему результату (x ~ a2). Следовательно, среднее смещение пропорционально средней энергии гармонического осциллятора

<х> ~ <E>,

а из статистической физики следует, что средняя энергия при тепловом равновесии пропорциональна температуре, <х> ~ <Е> ~ T, следовательно, и <x> ~ T, что объясняет нам линейное термическое расширение твердых тел.

§ 10 Адиабатические инварианты

Адиабатическими инвариантами называют физические величины, являющиеся функциями координат, скоростей и других параметров колебательных систем при условии актуально медленного изменения этих параметров:

f(k,ω,E, m, T,...).

105

Поставим задачу получить некоторые адиабатические инварианты. Запишем полную энергию системы, считая ее не (!) замкнутой Е ≠ cst, k - var

E = mv2/2 + kx2/2.

Возьмем первую производную по времени - t , учитывая,

что k = k (t)

dE/dt = mv dv/dt + kx dx/dt + (x2/2)dk/dt = v(ma + kx) + (x2/2)dk/dt =

(x2/2)dk/dt.

В круглых скобках стоят две силы одинаковые по величине и противоположные по направлению, имеем

dE/dt = (x2/2)dk/dt = (kx2/2) k dk/ dt = U ( x ) k dk/ dt.

Используем разложение в ряд вида

k dk / dt = (k dk / dt)0 (1 +α) dE/dt = U(x)( k dk /dt)0 (1 + α). (1)

Здесь записано разложение в ряд типа Тейлора и учтен первый порядок малости ( при dk/dt → 0 α → 0). (dk/ k dt)0 - значение выражения (1) в точке, выбранной за начало отсчета. Проинтегрируем (1) по времени от t до t + T(k). В нашем случае период Т является функцией k.

t +T(k) t +T(k)

∆E = (dk/ k dt)0 [∫ U(x(t′))dt′ + β], β = α ∫ U dt′ (dk/ k dt)0 → 0

Пусть для внутренней (потенциальной) энергии k = cst, а в выражении k dk/ dt - k и само это выражение перестало быть константой, в течение промежутка времени равного периоду Т. Это позволяет не утратить первоначальную зависимость k(t).

106

i)U = kx2/2

ii)x = a Cos(ωt + α)

iii)U = (ka2 /2) Cos2(ωt + α) = E Cos2(ωt + α) = E[1 + Cos(2ωt + α)]/2.

Вычислим отдельно интеграл при t = 0

T T

∫U dt′ = (E/2) ∫ [1 + Cos(2ωt′ + 2α)]dt′ = 0 0

TT

=(E/2)[∫dt′ + ∫ Cos(2ωt′ + 2α)dt′] =

0 0

T

= ET/2 + (1/2ω)Sin(2ωt +2α) | = ET/2. 0

Тогда

∆E = (dk/ k dt) (ET/2).

Заметим, что T dk/dt ∆k с точностью до величины более высокого порядка малости. Данное выражение равно приращению k за период T .

(k(t) = k0 + ∆t dk/dt + ∆t2d2k/2!dt2 + ..., здесь ∆t = T k k0 + T dk/dt T dk/dt k - k0 = ∆k)

Тогда

∆E = ∆k E/2k.

Осуществим предельный переход ∆ → d dE = E dk/2k dE/E = dk/2k.

Имеем дифференциальное уравнение с разделяющимися переменными, интегрируем

107

ln E = (1/2)ln k + cst ln E/√k = cst E/√k = cst.

Получили соотношение для адиабатических инвариант E и k. Это соотношение приводит также к

ω = √k/m √k = ω√m E/ω = cst и T = 2π√m/k √k = 2π√m/T ET = cst.

Пример: при медленном укорочении нити математического маятника его период колебаний медленно уменьшается и одновременно возрастает энергия, а произведение ЕТ - остается постоянным. Отличие от параметрических колебаний состоит в том, что там нить периодически удлиняется и укорачивается, то есть меняется не монотонно.

108

Часть 2 Молекулярная физика

Введение

Молекулярная физика объединяет разделы:

i)Собственно молекулярная физика - представление о веществе с позиций молекулярно-кинетической теории

ii)Физическая статистика – расчетный инструмент для изучения молекулярной физики (математическая база)

iii)Термодинамика - учение о тепловом движении

iv)Физическая кинетика - изучение процессов движения молекул в веществе (газах и твердых телах). (Две небольшие главы посвящены гидродинамике – изучению движения жидкости как континуальной субстанции, а также строению и свойствам кристаллов).

Основные понятия молекулярной физики - микрочастица и динами-

ческая система. Динамическая система представляет собой собрание микрочастиц (в газе, твердом или, как говорят, конденсированном теле, жидкости) молекул, атомов, ионов, ядер атомов, нейтронов, протонов, электронов,... . Однако, как правило частицы, о которых идет речь в молекулярной физике не заряжены или электромагнитным взаимодействием между ними можно пренебречь.

Атомистические представления впервые зародились в экспериментальной химии. Сформулируем два положения:

1.Общий вес, участвующих в химических реакциях веществ остается неизменным

2.Вещества вступают в реакции в одних и тех же простых весовых отношениях (Закон кратных отношений)

Пример:

2 части водорода + 16 частей кислорода = 18 частей воды (остальное, если оно и есть не востребуется)

109