Мальханов - Общая Физика

dS

R r

r +dr

Через кольцо (как это показано на рисунке) за 1с пройдет объем жидкости равный произведению площади кольца dS на среднюю скорость движения жидкости в точках кольца (v = l /t).

Замечание: в данном случае dQ - поток в единицу времени, м3/с, но если домножить его на плотность (что всегда можно сделать, так как плотность не меняется), то получим - м3 кг/с м3 = кг/с, то есть - ежесекундную массу. Итак

dQ = dS v(r) = 2πrdr v(r).

Подставим v (r) из (2)

dQ = vмакс (1 - r2/R2) 2πrdr

R R

Q = vмакс 2π∫ (1 - r2/R2)rdr = 2πvмакс [(r2/2) - (r4/4R2)] | = vмаксπR2/2 = 0 0

=vмакс S/2.

Подставим значение vмакс из (2)

Q = (P1 - P2)SR2/8ηl.

Полученное выражение носит название формулы Пуазейля. С учетом S = πR2 можно получить выражение вида

Q = (P1 - P2) S2/8ηlπ.

Из формулы Пуазейля следует, что поток жидкости прямо пропорционален перепаду давления на единицу длины при прочих равных условиях

Q (P1 - P2)/l.

190

Расчет кинетической энергии потока жидкости

dK = dm v2(r)/2

dm = ρdV, dV = dS v (r), dS = 2πrdr dm = ρ v (r) 2πrdr

dK = πρ v3rdr.

Используем выражение (2) и для расчета кинетической энергии останется вычислить интеграл

K = ρπ(∆P R /4ηl)3 ∫ (1 - r2/R2)3 rdr ([K] = Дж/с).

Работу, совершаемую жидкостью при движении можно вычислять по формуле

A = ∫ ∆P dV.

Чтобы перейти к интегрированию по радиальной координате (так как скорость зависит только от нее) произведем замену, получим

dV = v 2πrdr ([V] = м3/с), A = 2π ∆P ∫ vrdr =

= π ∆P2 R2/2ηl ∫ (1 - r2/R2)rdr.

Эффект Магнуса. (М. Генрих, 1802 - 1870, немецкий физик)

Здесь скорость больше, давление меньше

Здесь скорость меньше, давление больше

Цилиндрическое тело приводится во вращательное движение внутренними средствами. Оно находится под воздействием потока частиц слева на рисунке (ветер). Возникает сила, действующая перпендикулярно направлению потока частиц, определяемая разностью давлений.

191

Глава 6 Строение и свойства кристаллов

§ 1 Простые кристаллические структуры. Плотность кристаллов и межатомные расстояния

Твердые тела подразделяются на тела аморфные и кристаллические. В кристаллических телах из атомов образуется регулярный строй, неизменный во времени. Этот

регулярный строй (расположение) атомов в твердых телах называют кристаллической структурой. Иногда говорят: кристаллическая решетка или просто решетка. При этом говорят о регулярном (правильном) дальнем порядке расположения атомов, тогда как у аморфных тел реальным является только ближний порядок. Следует иметь в виду, что в реальных кристаллах дальний порядок реализуется лишь в относительно небольших областях - зернах. На границах таких зерен порядок меняется. Размер зерен составляет доли миллиметра. Если оценить межатомные расстояния (постоянную решетки) как 10А, тогда как 0,1 мм = 106 А, то количество атомов в такой цепочке составит 105 штук. Мы будем идеализировать весь кристалл, считая его бесконечным (подспудно подразумевая зерна).

1.1 О простых кристаллических структурах

Атомам надо упаковаться в твердом теле наиболее плотно (вследствие сил взаимодействия), иначе твердые тела распадутся, и не будут таковыми. Существуют различные виды связей атомов и молекул. Здесь мы будем априорно предполагать наличие таких связей.

Перечислим наиболее часто встречающиеся кристаллические структуры: ПК - простая кубическая структура - атомы находятся в вершинах куба.

ОЦК - объемно-центрированная кубическая структура - к ПК добавлен атом в геометрический центр куба.

192

ГЦК - гранецентрированная кубическая структура - к ПК добавлено по атому в центр каждой грани.

ГЕКС - гексагональная структура с плотной упаковкой - слои шестиугольных тетраэдров с атомами в вершинах правильных шестиугольников.

Существует также много других структур.

Остановимся подробней на структуре типа алмаза. Структура типа алмаза образуется из гранецентрированной кубической решетки. Атом в одной из вершин куба и три ближайших соседних атома такой решетки, расположенные в соседних гранях куба, сходящихся к этой вершине, образуют правильный тетраэдр. В центре этого правильного тетраэдра помещается еще один атом. Также необходимо поступить и с тетраэдрами образованными у других вершин куба.

193

1.2 Плотность кристаллов и межатомные расстояния

Координационное число – число ближайших к данному атому соседних атомов, тогда

Природа устроена так, что при различных упаковках решетка в целом энергетически находится (для каждой отдельной упаковки) в своем равновесном состоянии. Чем меньше координационное число, тем больший объем приходится на один атом и тем более «рыхлой» является упаковка. Пример: - α и γ - железо.

194

Скачек постоянной решетки плотности

aFe ρFe

900 T,°C 900 T,°C

Плотность кристалла можно связать с таким микроскопическим параметром как постоянная решетки. Постоянная решетки совпадает по смыслу с расстоянием между ближайшими соседними атомами только в случае простой кубической решетки. Ограничимся в данном случае представлением о постоянной решетки, как о некоем характерном расстоянии между соседними атомами в кристалле, тогда

V = a3,

где V - некоторый характерный элементарный объем в кристалле.

ρ = m/V = m/a3 = nM/NАa3

m - масса атомов в данном элементарном объеме

M - молярная масса (или атомная)

NA - число Авогадро, M/NА – масса одного атома

n - количество атомов, приходящихся на данный элементарный объем (элементарную ячейку).

Более точно пишут:

ρ = nM/kNAa3 a = (n M/k NAρ)1/3,

в нашем случае k = 1.

Определим n для простой кубической ячейки. Для наглядности представим атомы в решетке согласно рисунку

195

Для простой кубической ячейки за элементарную ячейку можно принять кубик, в вершинах которого находятся атомы. Каждый атом в вершине на 1/8 часть

принадлежит кубической ячейке, тогда, поскольку всего таких атомов 8 , име-

ем n = 1.

Для ОЦК - решетки прибавится еще один атом в центре. Итого будет n = 2. Рассчитаем постоянную решетки для ОЦК решетки железа (т.е. α - Fe) .

a3 = n M / k NAρ 2 56 10-3/1 6,02 1023 7,88 103 2 10-29 м 3a 0,287 10-9 м = 0,287 нм = 2,87 A.

Замечено, что ГЦК - решеткой обладают благородные газы и большинство металлов. В таблице приводятся постоянные решетки для некоторых элементов

196

§ 2 Решетка Бравэ и ячейка Вигнера -Зейтца

Необходимо более строго определить элементарную ячейку в кристалле иначе называемую примитивной ячейкой.

Примитивная ячейка:

такой минимальный объем пространства кристалла, который при всех возможных трансляциях заполнит пространство до бесконечности

R - вектор трансляции, ai - базовые вектора (одновременно все три - некомпланарные). Для произвольной точки трехмерного пространства можно записать

R = n1a1 + n2a2 + n3a3. (1)

ni - целые числа.

Первое определение решетки Бравэ:

бесконечная периодическая структура, образованная дискретными точками (узлами, атомами) и имеющая абсолютно одинаковый пространственный порядок и ориентацию независимо от исходной точки.

Второе определение решетки Бравэ:

трехмерная решетка Бравэ образована всеми точками с радиусвекторами R вида (1).

Термин “решетка Бравэ” применяется как ко множеству точек, так и ко множеству векторов, соединяющих эти точки. Иногда говорят, что решетка Бравэ понимается как множество трансляций, определяемых векторами.

Теперь можно вернуться к определению примитивной (элементарной) ячейки, основываясь на том, что параллельным переносом такой примитивной ячейки может быть образована вся решетка Бравэ.

Определение примитивной ячейки:

объем пространства, который, будучи подвергнут всем трансляциям, образующим решетку Бравэ, заполнит все пространство, нигде не перекрываясь и нигде не оставляя пустот.

197

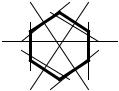
Выделить примитивную ячейку не всегда легко. Это, вообще говоря, самостоятельная задача, так как существует множество разных и подчас очень сложных решеток. Ячейка Вигнера-Зейтца – одна из них: (обладает полной симметрией решетки Бравэ)

Определение.

Ячейка Вигнера-Зейтца - наименьший многогранник, ограниченный плоскостями, проведенными через середины прямых, соединяющих ближайшие узлы.

На плоском рисунке плоскости заменены прямыми. Если в пространстве попытаться изобразить для ОЦК - решетки примитивную ячейку, то получим усеченный октаэдр.

Специалисты по физике твердого тела чаще интересуются всеми указанными построениями в пространстве - обратном линейному пространству. Это связано с тем обстоятельством, что в таком обратном пространстве проще перейти к пространству энергии и импульса для микроскопических объектов типа атом, электрон, фотон, а также квазичастиц: дырка, фонон, полярон и т.п. . При этом расчеты ведутся по формулам

k =2π/λ, p = ћk =2π/λ , ε = hν = hc/λ.

Здесь λ - длина волны, k - волновое число, p,ε - импульс и энергия частиц, ћ = h/2π - постоянная Планка.

Замечание о терминологии: Когда говорят “элементарная” или “условная” ячейка, то при этом не подразумевается примитивная ячейка. Обратная ячейка всегда определена по отношению к конкретной прямой решетке Бравэ.

198

§ 3 Кристаллические системы

Рассмотрим все возможные типы симметрий решеток Бравэ по отношению к поворотам и отражениям. Такие типы симметрий носят название кристаллических систем или сингоний. Каждая из них представляет собой определенную совокупность осей и плоскостей симметрии.

1. Триклинная система (наименее симметричная из всех)

α

β γ

Гt

Параллелепипед с произвольными ребрами и углами α ≠ β ≠ γ, a ≠ b ≠ c, t - триклинная, 1 штука

2. Моноклинная система

На боку- - прямой

β

b

Гm, Гm

Прямой параллелепипед с произвольными основаниями α = γ = π/2, β ≠ π/2, a ≠ b ≠ c, m - моноклинная, Гmb - с атомами в двух гранях (центрированными основаниями), b - базовая, 2 штуки.

3. Ортогональная система (или ромбическая)

199