Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Фишбейн, тесты

.pdf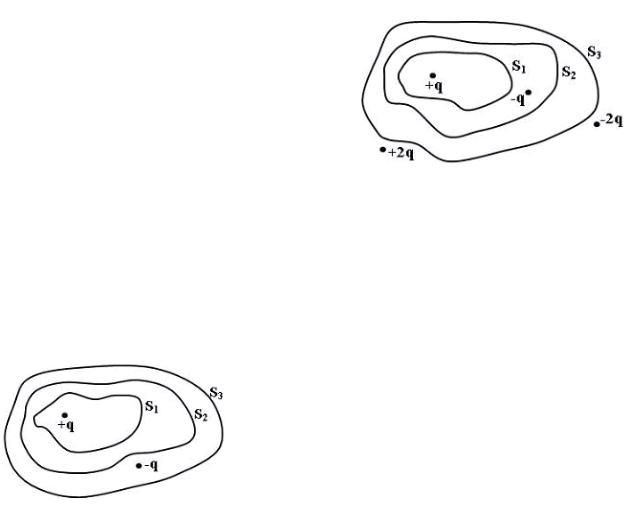

Скачиваний:

241

Добавлен:

17.05.2015

Размер:

1.1 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

15. Система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3 даны на рисунке. Поток вектора напряженности электрического поля равен нулю через поверхности

1– S1

2 – S2

3 – S3

Решение

По теореме Гаусса поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен отношению суммарного заряда охватываемого поверхностью и электрической постоянной. Таким образом, поток равен нулю, если суммарный заряд равен нулю. Правильный ответ 2 и 3.

16. Система точечных зарядов в вакууме и замкнутые поверхностиS1, S2 и S3 даны на рисунке. Поток вектора напряженности электрического поля отличен от нуля через -по верхности

1– S1

2 – S2

3– S3

Решение

По теореме Гаусса поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен отношению суммарного заряда охватываемого поверхностью и электрической постоянной. Таким образом, поток не равен нулю, если суммарный заряд не равен нулю. Правильный ответ 1 и 2.

17. Точечный заряд+ q находится в центре сферической поверхности. Если уменьшить радиус сферической поверхности, то поток вектора напряженности электрического поля через поверхность сферы

1 – уменьшится,

2 – увеличится,

3 – не изменится.

Решение

По теореме Гаусса поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен отношению суммарного заряда охватываемого поверхностью и электрической постоянной. Следовательно, поток не зависит от формы и размеров поверхности, если не меняется заряд внутри ее. Правильный ответ 3 – не изменится.

18. Точечный заряд + q находится в центре сферической поверхности. Если заряд сместить из центра сферы, оставляя его внутри нее, то поток вектора напряженности электрического поля через поверхность сферы

1 – не изменится,

2 – увеличится,

3 – уменьшится.

Решение

По теореме Гаусса поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен отношению суммарного заряда охватываемого поверхностью и электрической постоянной. Следовательно, поток не зависит положения заряда внутри поверхности. Правильный ответ 1 – не изменится.

19. Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд –q внутрь сферы, то поток вектора напряженности электрического поля через поверхность сферы

1 – уменьшится,

2 – увеличится,

3 – не изменится.

Решение

По теореме Гаусса поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен отношению суммарного заряда охватываемого поверхностью и электрической постоянной. Заряд (и поток) был положительный, а после добавления отрицательного заряда стал нулевой. Правильный ответ 1 – уменьшится.

20. Относительно статических электрических полей справедливо утверждение:

1 – электростатическое поле действует как на электрические, так и на магнитные заряды,

2 – электростатическое поле является потенциальным, 3 – поток вектора напряженности электростатического поля сквозь произвольную замкнутую поверхность всегда равен нулю.

Решение

Электростатическое поле не действует на магнитные заряды, которых нет. Первое утверждение не верно.

Электростатическое поле является потенциальным. Второе – верно. Поток вектора напряженности электростатического поля сквозь произволь-

ную замкнутую поверхность равен отношению суммарного заряда охватываемого поверхностью и электрической постоянной, а не «всегда равен нулю». Третье утверждение не верно.

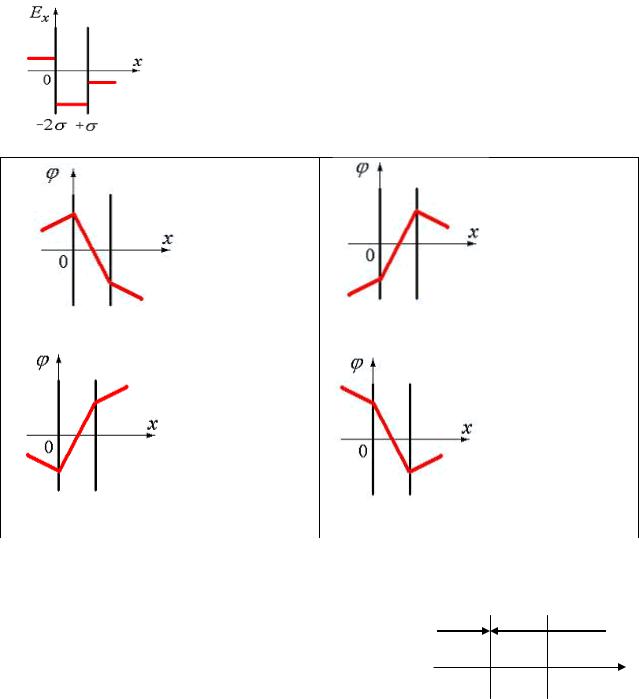
21. Электрическое поле создано двумя параллельными плоскостями, заряженными с поверхностными плотностями –2σ и +σ. Нарисунке показана качественная зависимость проекции напряженности от координаты х вне пластин и между пластинами. Правильно отражает характер изменения потенциала φ этого поля гра-

фик

на рис. а на рис. б на рис. в на рис. г

φ		φ

		Рис. а		Рис. б


		φ		φ
		φ		φ
		φ

Рис. в				Рис. г

Решение
Там,	где	положительно	направлено по
оси х, а там где отрицательно– против				. Так как
вектор	направлен в сторону		уменьшенияφ, то
слева направо		до первой плоскости φ уменьшается,

а далее слева направо– возрастает. Следовательно, правильный – рис. в.

22. Электрическое поле создано двумя параллельными плоскостями, заряженными с поверхностными плотностями +σ и –2σ. Качественная зависимость потенциала поля φ от координаты х вне пластин и между пластинами правильно показана на графике

рис. а, рис. б, рис. в, рис. г.

+ –

Рис. б

Рис. а

+σ

–

+σ

–

Рис. в

Рис. г

Решение

Первый способ. Потенциал не может изменяться скачком. Таким обра-

зом, правильное решение представлено на рис. а.
Второй способ. Определяем направление вектора				во всех областях
пространства. Так как поле каждой плоскости однородно и			вектора		направле-
ны вдоль одной прямой, то		результирующий вектор рез	направлен		вдоль на-
правления большего по модулю вектора, т. е. вектора поля				отрицательного за-
ряда (сплошная линия).		рез
+	−2

Так как вектор	направлен в сторону уменьшения φ, то слева направо до вто-
рой плоскости φ	уменьшается, а далее слева направо– возрастает. Следова-

тельно, правильный – рис. a.

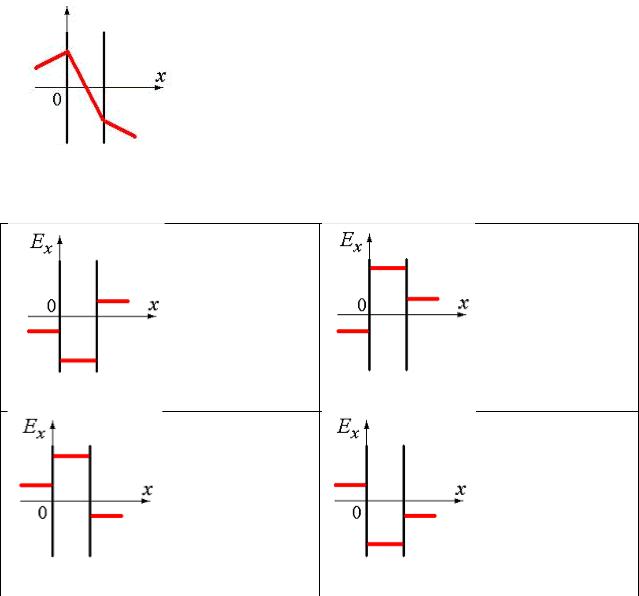
23. Электрическое поле создано двумя параллельными плоскостями, заряженными с поверхностными плотностями–2σ и +σ. На рисунке дана зависимость изменения потенциала φ этого поля от координатых вне пластин и между пластинами. Правильно отражает качественную зависимость проекции напряженности поля Ех на ось х график

+2 –σ

на рис. а, на рис. б, на рис. в, на рис. г.

Рис. а

Рис. б

Рис. в		Рис. г

Решение
Так как вектор	направлен в сторону уменьшения φ то вектор			слева
от начала координат(первой		плоскости) направлен влево,,	т. е. против	оси x

(Ех < 0), а справа – по оси x (Ех > 0). Следовательно, правильный график изображен на рис. б.

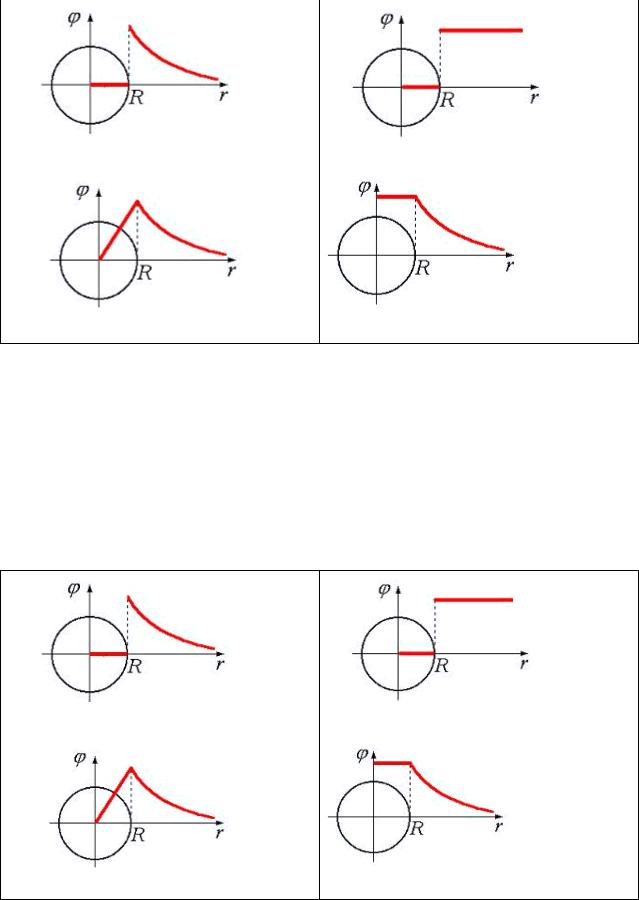
24. Зависимость потенциала электрического поляφ от расстояния r между центром равномерно заряженной проводящей сферы радиусом R и точкой, где определяется потенциал, правильно изображена на графике

	рис. а,	рис. б,	рис. в,	рис. г.


φ
φ			φ

Рис. а		Рис. б


		φ
	φ	φ

Рис. в

Рис. г

Решение

Потенциал поля не может измениться скачком: значит рис. в или г. Сфера и все пространство внутри нее – одна сплошная эквипотенциальная поверхность, т. е. правильный график на рис. г. (Видимо заряд на сфере положительный).

25. Зависимость потенциала электрического поля φ от расстояния r между центром равномерно заряженного проводящего сплошного шара радиусом R и точкой, где определяется потенциал, правильно изображена на графике

рис. а, рис. б, рис. в, рис. г.

φ
φ		φ

Рис. а		Рис. б


		φ
	φ	φ

Рис. в

Рис. г

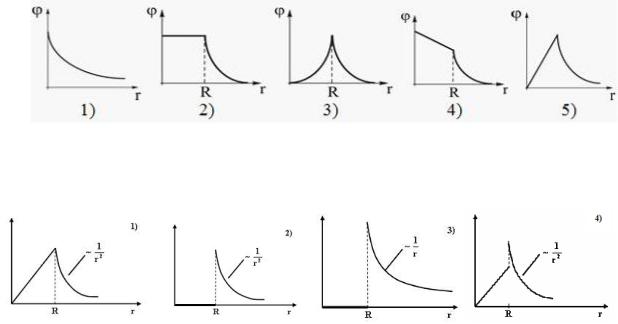
Решение Примечание. «…равномерно заряженных проводящих сплошных шаров» не

бывает. Или равномерно заряженный по поверхности проводящий шар или равномерно заряженный по объему не проводящийшар. В первом случае правильный ответ дан на рис. г, во втором – на рис. в (без учета ε). На сайте www.i-exam.ru ответ – в.

26.Электростатическое поле созданоположительно заряженной сферой.

Правильно отражает зависимость потенциала от расстояния рисунок …2).

27. На рисунках представлены графики зависимости напряженности поляE(r) для различных распределени:

График зависимости E(r) для шара радиуса R, равномерно заряженного по объему, показан на рисунке …1). (Без учета ε).

28. Два проводника заряжены до потенциалов30 В и –20 В. Заряд 100 нКл переносят с первого проводника на второй. При этом силы поля совершают работу (в мкДж), равную …5.

Решение

Считаем, что потенциалы проводников остаются неизменными.

Тогда

A	= q(j - j		) 100= ×10-9 (30 - (-20)) =5 ×10-6 = 5 мкДж.
12	1	2

29. Заряд 1 нКл переместился из точки, находящейся на расстоянии 1 см от поверхности заряженного проводящего шара радиусом 9 см, в бесконечность. Поверхностная плотность заряда шара1,1·10-4 Кл/м2. Работа сил поля (в мДж), совершаемая при этом перемещении, равна …1. (Ответ округлите до целых.)

Решение
Работа	сил	поля по перемещению	заряда определяется по формуле
A12 = q(j1 - j2 ) , где q – перемещаемый заряд, j1			и j2 - потенциалы начальной
и конечной	точек	соответственно. В нашем случае – потенциал в начальной
точке и на бесконечности.

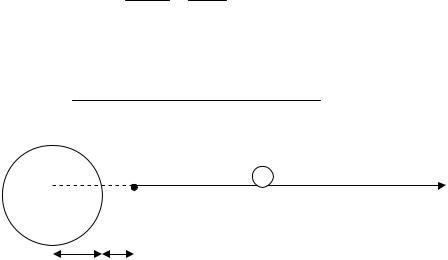
Учтем, что площадь поверхности шара равна 4pR2 .Тогда имеем

j = j(¥) = 0 , j

1 =

s4pR 2

и A = q(j - j

) =

qs4pR 2

4pe0 r 4pe0 (R + a)

4pe0 (R + a)

Здесь R = 9см, a =1см, s = 1,1·10-4 Кл/м2 и

A12 =

×109

×10-9 ×1,1×10-4 × 4p×81×10-4

1,0 ×10

-3

Дж =1мДж.

10-1

ЗАКОНЫ ПОСТОЯННОГО ТОКА

Электрический ток – упорядоченное движение заряженных частиц. Направление тока – направление движение положительно заряженных частиц.

Сила тока I

Для постоянного тока

				I =	q	, [А] q = I t .
				I =		, [А] q = I t .
Для переменного тока					t
Для переменного тока				t2
	dq		2	t2
I =	dq	, q12 =	òdq =òIdt - площадь под кривой I от t ,
I =		, q12 =	òdq =òIdt - площадь под кривой I от t ,
	dt		1	t1

где q -заряд, [Кл].

Плотность тока j

j = I , [А/м2]. S

где S - площадь сечения проводника, [м2].

Закон Ома в локальной форме

j = sE = Er ,

где s-удельная проводимость, r -удельное сопротивление, [Ом·м], E - напряженность электрического поля внутри проводника, [В/м].

j = q0n u ,

где q0 -модуль заряда заряженных частиц(электронов) в проводнике ( q0 = e ), n -концентрация заряженных частиц (электронов) в проводнике, u -средняя

скорость упорядоченного движения заряженных частиц(электронов) в проводнике (скорость дрейфа).

R = r l , S

где R – сопротивление проводника, [Ом], l и S – длина и площадь поперечного сечения проводника.

r = r0 (1 + at) , R = R0 (1 + at),

где t - температура в С ° , r0 и R0 – удельное сопротивление и сопротивление при t = 0°, a [град-1 ].

r, R

r0 , R0

t°

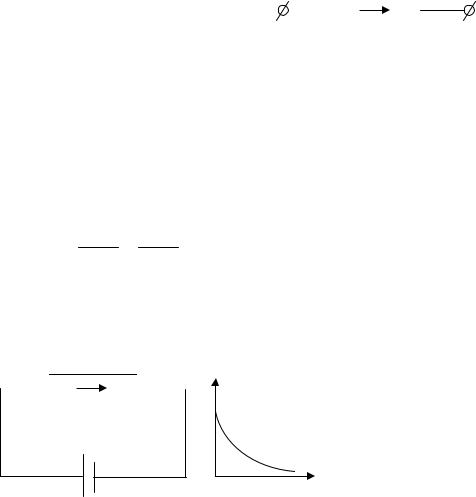
Закон Ома для однородного участка цепи

I =	U	, U = El,	I	U
	U		I
	R


				R
				R

где U -напряжение (разность потенциалов), [B], E - напряженность электрического поля в проводнике, l -длина проводника.

Закон Ома для замкнутой (полной) цепи

I =

e IR=+ Ir =U

R + r

R =

1 =

<1, I

= I

max

кз

R + r

где e -ЭДС, [B], h- КПД схемы (источника), Iкз - ток короткого замыкания.

I	U R	I			e
I	U R	I
		I		=
	R		max
	R				r
					r

Мощность P и работа A тока на однородном участке цепи

P =UI.

Постоянный ток	Переменный ток
	t	t
A = Pt = UIt.	A = òPdt = òUIdt.
	0	0
Мощность P и работа A тока в замкнутой цепи
	P = eI.
Постоянный ток	Переменный ток
	t	t
A = =Pt eIt	A = ò=Pdt	òeIdt.
	0	0

Здесь A - работа сил тока, [Дж], P - мощность сил тока, [Дж/с] = [Вт].

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2018612.35 Кб3Фин-эконом расчеты_пособие.doc
#
17.05.20152.25 Mб1Фирменная молодежь. Выпуск 1.pdf
#
17.05.2015522.63 Кб36Фишбейн, колебания.pdf
#
17.05.20151.09 Mб67Фишбейн, механика.pdf
#
17.05.2015555.17 Кб96Фишбейн, термодинамика.pdf
#
17.05.20151.1 Mб241Фишбейн, тесты.pdf
#
17.05.2015300.03 Кб6ФК 1 курс 14-15.doc
#
09.11.201861.95 Кб6ФМН методичка 2010-11.doc
#
17.05.2015492.33 Кб125ФНП скачков.pdf
#
16.11.201882.43 Кб5фома аквинский.doc
#
17.05.201517.33 Кб105форма-наряда допуска.docx