4.4 Для самостоятельного изучения

4.4.1. Применение законов сохранения к упругому и неупругому соударению двух тел.

При соударении тела деформируются. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергиютел.

Столкновения могут быть упругими и неупругими. Их предельные идеализированные случаи – абсолютно упругий и абсолютно неупругий удар.

При абсолютно упругом ударе (например, столкновении шаров из слоновой кости или закаленной стали) механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия тел полностью или частично переходит в потенциальную энергию упругой деформации. По завершении удара первоначальная форма тел полностью восстанавливается. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию и тела разлетаются со скоростями, величина и направление которых определяются законом сохранения механической энергии и законом сохранения полного импульса системы тел.

Пpи неупругом ударе (например столкновении шаров из воска, двух разноименных ионов с образованием молекулы, захвате свободного электрона положительным ионом и т.д.) тела не восстанавливают свою первоначальную форму, кинетическая энергия тел частично или полностью превращается во внутреннюю энергию. При абсолютно неупругом ударе тела движутся после удара как единое целое с одинаковой скоростью или покоятся. При абсолютно неупругом ударе закон сохранения механической энергии не соблюдается. Выполняется лишь закон сохранения импульса и закон сохранения суммарной энергии различных видов – механической и внутренней.

Рассмотрим случай центрального соударения двух однородных шаров. Удар называется центральным, если шары до удара движутся вдоль прямой, соединяющей их центры (рис 4.12).

Поскольку удар упругий, то механическая энергия не переходит в другие виды энергии а кинетическая энергия сохраняется:

, (4.9)

где ,,,– скорости шаров до и после удара.

Потенциальная энергия при упругом столкновении шаров не меняется закон сохранения импульса:

, (4.10)

Уравнения (4.9) следует:

,

=

. (4.11)

Из уравнения (4.10) с учетом проекции скоростей на ось Х:

. (4.12)

Поделив левые и правые части уравнении (4.11) (4.12), получим:

(4.13)

Подставим (4.13) в (4.12):

,

.

. (4.14)

По аналогии, подставим в формулу (4.13) полученное значение для :

. (4.15)

Рассмотрим частные случаи.

1. Массы шаров равны .

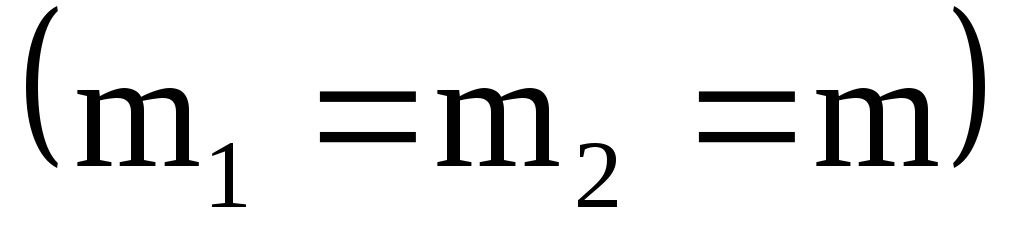Тогда

,

.

Если до столкновения второй шар покоился , то после столкновения первый шар остановился, а второй будет двигаться со скоростью.

2) Масса второго шара значительно больше массы первого (т₂>> т₁). Разделим числитель и знаменатель выражений (4.14) и (4.15) наm₂:

;

.

Отношением m₁/m₂пренебрегаем. Тогда,, т.е. скорость большого шара практически не меняется.

Если массивный шар покоился , то он покоится и после удара, а малый шар будет иметь скорость. Такой тип столкновения рассматривается при расчете давления, оказываемого молекулами газа на стенки сосуда.