Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

tezisu

.pdf

Скачиваний:

Добавлен:

17.05.2015

Размер:

7.29 Mб

Скачать

☆

<<< < Предыдущая 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3728 29 30 31 32 33 34 35 36 37 > Следующая >>>

где u = u(n) – функциональный параметр – векторно-значная функция дискрет-ного аргумента n, λ – спектральный параметр, Z diag( 1 , 2 ,..., N ) – диаго-нальная матрица, показатели γi – целые числа, γ1 < γ2 <…< γN . Введем операторы сдвига Dn, Dm, действующий по правилу

Dnt(n, m)= t(n+1,m), Dmt(n, m)= t(n, m+1).

Гипотеза. Рассмотрим дискретный оператор L Dn 1P(u(n), )Z .

Предположим, что для любого целого n функция P(u(n), λ) является аналитической в некоторой окрестности точки λ = ∞ (или λ = 0), и все

главные	миноры матрицы P(u(n),		∞) (или P-1(u(n), 0)) отличны от нуля.
Тогда существует формальный ряд			T Ti i (или	T Ti i ) такой, что
			i 0	i 0
оператор	L T 1LT имеет вид	L D 1hZ , где h		– формальный ряд с
	0	0	n
диагональными коэффициентами.
Для построения законов сохранения динамической системы (1)
рассмотрим операторы L D 1PZ и			M D 1R . Доказано, что если оператор
	n		m

P удовлетворяет условию Гипотезы, и функция R мероморфна в окрестности точки λ = ∞, то операторы L и M приводятся к диагональному виду при помощи одного и того же преобразования. Получим операторы L0 T 1LT и

M0 T 1MT , которые можно представить в виде формальных рядов L0 Dn 1hZ и M0 Dm1S с диагональными коэффициентами.

Окончательно, законы сохранения получаем из выражения

Dm 1 ln h Dn 1 ln S .	(2)
Полагая h = h0+h1λ-1+ h2λ-2+… и S = S0+S1λ-1+ S2λ-2+…,	равенство (2)
примет вид

		h	h		1	h		2
D 1 ln h		1		2			1		...	D 1 ln

m	0	h	h		2		h			n

		0		0			0

	S		S	2	1	S		2
S0		1		2			1		...
S0	S		S		2	S			...
	S		S		2	S
		0		0			0

Литература

[1]. В.Вазов, Асимптотическое разложение решений обыкновенных дифференциальных уравнений. М., Мир, 1968.

[2]. И.Т.Хабибуллин, Дискретная система Захарова-Шабата и интегрируемые системы, Записки научных семинаров Ломи, Ленинград,

Наука, Т.145, 1985.

271

УДК 517.95

- PSEUDO-DIFFERENTIAL OPERATORS

Niyaz Tokmagambetov

Al-Farabi Kazakh National University,

Almaty, Kazakhstan

Pseudo-differential operators and –toroidal symbols generated by a non– local boundary value problem are investigated. Formula for compositions with pseudo-differential operators generated by a non–local boundary value problem is

derived. In the Hilbert space 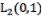concepts of the Fourier transform and convolution generated by a non–local boundary value problem are introduced.

Let us introduce in the Hilbert space 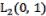the differential operator

with the domain where 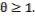The symbolic analysis on commute with the classical Fourier transform, which is a


unitary transform in the Hilbert	space	It is generated			by	the
operator of differentiation	because	the system	of	exponents
is a system of "eigenfunctions" corresponding					to	its
continuous spectrum. Instead of	the differential	operator	in	the space

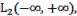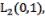consider an operator in the Hilbert space which is generated by the differential operator 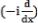and non–local boundary condition

Indeed, we start an direction of discrete analysis based on elliptic boundary value problems, continuing, in a sense, the analysis on the torus started by M. Ruzhansky and V. Turunen [1], in which case one may think of a problem having periodic boundary conditions.

References

[1] M. Ruzhansky, V. Turunen, Quantization of Pseudo-differential Operators on the Torus, J. Fourier Anal. Appl., 16, 943–982 (2010).

272

УДК 517.9

ЛИНЕЙНЫЕ ГИПЕРБОЛИЧЕСКИЕ СИСТЕМЫ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

Воронова Юлия Геннадьевна2 Уфимский государственный авиационный технический университет,

г. Уфа, Россия

В работе рассматривается система уравнений вида

	2						(1)
		U a		U b		U cU 0,
	x y		x		y
где a,b, c - постоянные			матрицы второго порядка, U - столбец

неизвестных U1(x, y),U 2 (x, y) T .

Мы предполагаем, что для системы уравнений (1) выполнены условия существования и единственности обобщенных инвариантов Лапласа [1]. Получен общий вид обобщенных инвариантов Лапласа для линейных систем уравнений (1):

Теорема. Пусть инварианты Лапласа H1, H2 , , Hk уравнения (1) – невырожденные матрицы, а RangHk 1 1. Тогда обобщенный инвариант порядка n вычисляется по формуле

X	n	(, )n k 1 X				k 1	, n k 1, k 2,

здесь ( ,			2	), ( ,	2	), H		k 1	T .
1				1

Описаны системы уравнений (1), для которых обобщенные инварианты Лапласа есть нулевые матрицы и для них построено общее решение. Также проведена классификация систем уравнений третьего порядка с постоянными коэффициентами, у которых инвариант H1 имеет ранг 2, а

обобщенный инвариант Лапласа X 2 0 .

Литература

[1] Жибер А.В., Соколов В.В. Точно интегрируемые гиперболические уравнения лиувиллевского типа. УМН. – 2001. – Т. 56. – №1. – С. 63 - 106.

2 Работа поддержана грантом РФФИ № 14-01-97008 р-поволжье-а

273

СЕКЦИЯ «СПЕКТРАЛЬНАЯ ТЕОРИЯ ОПЕРАТОРОВ»

УДК 517.984:517.928.8

АСИМПТОТИКИ СОБСТВЕННЫХ ЗНАЧЕНИЙ ЭЛЛИПТИЧЕСКОЙ

КРАЕВОЙ ЗАДАЧИ В ОБЛАСТИ С МАЛЫМ ОТВЕРСТИЕМ

Давлетов Д.Б. 1, Файзулина К.И.2 1 Башкирский государственный педагогический университет, г. Уфа, Россия,

2 Башкирский государственный университет, г. Уфа, Россия

Пусть

, –

ограниченные

связные

области

Rn , n 3 ,

содержащие начало координат, ,

C ,

– площадь единичной

Rn , c 0 -

a C

сферы в

гармоническая емкость

aij a ji ,

2 , 1, 2 0 , x , 1,..., n ,

2 aij x i j

i, j 1

x : 1x , \ , а 0 1 . Доказана теорема.

Теорема 1. Пусть 0 – двукратное собственное значение краевой

задачи:

a x

a x u u ,

x ,

u 0 ,

x ,

0 0

i, j 1

2 –

соответствующие

ортонормированные

собственные

функции

такие,

что

1 0 0

2 0 0 .

Тогда

существуют

два

простых собственных

значения

краевой

задачи:

a x u u ,

x ,

u 0 ,

x ,

i, j 1

сходящиеся к 0 , и они имеют следующие асимптотики соответственно:

d n

2 n 2

n 2

i n 2,0

i 2

n 2

, p 1

i 0

p 0 i n 2

274

			2	d n			2 n	2 2										2
0	n	i	2				2 n	2 2	ln						i	ln	p	2
0		i n,0							ln							ln		i 2 n 2 2, p 1 ,
		i 0								p 0 i		n 2 p
				1		n 2 c				Sn		1	0			2
				1								1				2
			n 2,0									0				,
			2		Sn		2					2		0 0 ,
			2				2					2
где C2			n.0			0		0 C2 0
где C2		– положительно					определенная				(n n) -матрица, зависящая
только от геометрии ,						а	d n 0 при				нечетных							n и d n 1 при

четных n .

Давлетов Д.Б., Файзулина К.И., 2014 г.

275

УДК 517.929.8:517.984

ЗАДАЧА СТЕКЛОВА В ПОЛУЦИЛИНДРЕ С МАЛЫМ ОТВЕРСТИЕМ

Кожевников Денис Владимирович, Хуснуллин Ильфат Хамзиевич Башкирский государственный педагогический университет им. М.Акмуллы, г. Уфа, Россия

Пусть -

(n 1) -мерная

ограниченная

область, n 3 ,

C ,

:= (a, ) ,

a < 0 ,

{0} ,

- ограниченная

область

Rn ,

C ,

= {x : 1x },

0 1,

:= \ ,

| S

| -

площадь единичной сферы в Rn , c( ) 0

- емкость области . Методом

согласования асимптотических разложений [1] доказана

Теорема 1.1 Пусть 0

- простое собственное значение краевой задачи

=0,

x ,

=0,

x \

, x

: a ,

- соответствующая нормированная в

L2 ( a )

собственная функция.

Тогда

собственное

значение

краевой

задачи

=0, x

=0,

сходящееся к

при

имеет

асимптотику

где

i n 2

i =0

c( )

(n 2) 2

(0).

Причем,

если

(0) = 0

то

n 2

n 2 n 1

0 ,

n =

0 (0)C( ) 0 (0),

где C( )

симметричная

положительная

n n -матрица,

компоненты

которой

зависят только геометрии области .

Работа

второго

автора

выполнена

рамках

базовой

части

государственного задания в сфере научной деятельности Минобрнауки России.

Литература

1. Ильин А.М. Согласование асимптотических разложений решений краевых задач. М.: Наука. 1989. – 336.

276

УДК 517.9

ФОРМУЛА ЛЕФШЕЦА ДЛЯ ПОТОКА НА РАССЛОЕННОМ МНОГООБРАЗИИ.

Павленко Виктор Александрович Башкирский государственный аграрный университет, г.Уфа, Россия

Пусть компактное многообразие X является тотальным пространством

расслоения : X S1 над	окружностью.	Пусть на	X задан	поток
Tt : X X , сохраняющий	расслоение .	Гладкое	векторное	поле,

порождѐнное данным потоком, представляется в виде:

V ( y) v0 ( y) a( y) y ,

где v0 y – векторное поле, касающееся слоѐв расслоения . Предположим, что поток имеет конечное число неподвижных точек

1 ,..., k , которые являются невырожденными, что означает, j 1,..., k

справедливо a( j ) 0 , при этом a j 0 . Рассмотрим слоение ,

задаваемое слоями расслоения . Основной целью работы является написать формулу Лефшеца, которая связывает неподвижные точки и

замкнутые орбиты потока. Орбита потока	Tt называется замкнутой, если
0 , такое что T (x) x x X .	Числом Лефшеца потока Tt

определяется по формуле:

n 1 s

L(T ) ( 1)s tr(Tt* : H ( ) H s ( )) ,

s 0

где H s ( ) – послойные когомологии де Рама. Проблема заключается в том, что в данном случае оператор Tt* не является ядерным. Случай, когда

поток не имеет неподвижных точек, был рассмотрен Ю.А. Кордюковым и Х.Л. Альваресом. В нашем случае формула Лефшеца имеет вид:

	n 1
L(T ) С ( ) 0 , где	( 1)s dim H s (F ) .
	s 0

277

УДК 517.929.8:517.984

О ПОВЕДЕНИИ СОБСТВЕННОГО ЗНАЧЕНИЯ ПРИ СИНГУЛЯРНОМ ВОЗМУЩЕНИИ ЗАДАЧИ НЕЙМАНА ДЛЯ

ЛАПЛАСИАНА В КРУГЕ

Репьевский С.В.1, Гадыльшин Р.Р.2

1Челябинский государственный университет, г. Челябинск, Россия,

2Башкирский государственный педагогический университет им. М.

Акмуллы, г.Уфа, Россия

Пусть – круг единичного радиуса с центром в начале координат,

(r, ) - полярные координаты,									: {x : a b } ,						0 1,
a 0 b . Рассмотрим краевую задачу													0, x	,
					,		x ,						0, x	,

								0,		x \ . (1)

						r
						r
Хорошо известно (см. [1]), что собственные значения задачи (1) при
0 сходятся к собственным значениям задачи
	0	0	0	, x ,							0	0,	x ,		(2)
	0		0								0

Задача (2), в свою очередь, имеет либо простые собственные значения, совпадающие с квадратами нулей производной функции Бесселя нулевого порядка, либо двукратные собственные значения, совпадающие с квадратами нулей производной функции Бесселя m -го порядка, m 1 . Методом согласования асимптотических разложений [2] доказана следующая теорема.

Теорема 1. Существует собственное значение											краевой задачи (1),
сходящееся к двукратному собственному значению 0											краевой задачи (2),
						2i
которое имеет асимптотику			0 2 i ln k							i 2,k ,где
					i 0 k 0
2		m2 2		(a b)2 k 1					k	,	k 0 .
2							0			,	k 0 .
2 2k ,k m	1			8				4
		0		8		2

Литература

1.Гадыльшин Р.Р. Спектр эллиптических краевых задач при сингулярном возмущении граничных условий, Асимптотические свойства решений дифференциальных уравнений, Уфа, БНЦ УрО АН СССР, 1988,

C.4-16

2.Ильин А.М. Согласование асимптотических разложений решений краевых задач. М.: Наука. 1989. – 336.

278

УДК 517.929.8:517.984

АСИМПТОТИКА СОБСТВЕННЫХ ЗНАЧЕНИЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛАПЛАСИАНА В КРУГЕ СО СМЕНОЙ ГРАНИЧНЫХ УСЛОВИЙ

Шишкина Е.А.1, Репьевский С.В.2, Гадыльшин Р.Р.1 1 Башкирский педагогический университет им. М. Акмуллы, г. Уфа, Россия,

2 Челябинский государственный университет, г. Челябинск, Россия

Пусть – круг единичного радиуса с центром в начале координат,

(r, ) - полярные			координаты,			: {x : a b } ,			0 1,
a 0 b . Хорошо известно, что краевая задача на собственные значения
	0	0		0	, x ,		0	0, x .	(1)

имеет либо простые, либо двукратные собственные значения. Методом согласования асимптотических разложений [1] доказаны следующие теоремы.

Теорема 1. Собственное значение

краевой задачи

x ,

x \

, (2)

сходящееся

простому

собственному

значению

задачи

(1), имеет

(

)k 1 (b a)2(k 1)

асимптотику

2 i ln k i 2,k ,где 2 2k ,k

4k 3

i 0 k 0

k 0 .

Теорема

2. Собственные

значения

,(1) , ,(2)

краевой

задачи

(2),

сходящиеся к двукратному собственному значению 0

задачи (1), являются

простыми и имеют асимптотики

i 2,k ,

i 4,k

,(1)

(1)

,(2)

(2)

i 0 k 0

где

(2) 4 2k ,k

1. Ильин краевых задач.

(1)		( )k 1 (b a)2(k 1)			, k 0		,
(1)			0		, k 0		,
2 2k ,k
2 2k ,k				24k 3
m2	(a b)2		(5a2 6ab 5b2 ) k 1					2	k
0						0		0		, k 0 .
4				16		8		16
4				16		8		16

Литература

А.М. Согласование асимптотических разложений решений М.: Наука. 1989. – 336.

279

СЕКЦИЯ «МЕХАНИКА»

УДК 532.546

ФИЛЬТРАЦИЯ ЖИДКОСТИ В ТРЕЩИНОВАТО-ПОРИСТОЙ СРЕДЕ

Белова С.В.

Бирский филиал Башкирского государственного университета, г. Бирск, Россия

Внастоящее время добыча углеводородного сырья перемещается к месторождениям, с аномально низкими коэффициентами проницаемости порядка миллидарси и даже ниже этого значения. В связи с этим извлечение жидких углеводородов из коллекторов с супернизкими значениями коэффициента проницаемости становятся еще более проблематичным.

Вданной ситуации большую актуальность приобретают горизонтальные скважины и создание вокруг них систем трещин. При такой технологии жидкость в основной массе в скважины поступает через трещины.

Внастоящей работе полагая, что трещиновато-пористая среда представляет собой систему из блоков «столбов» или блоков «булыжников» построена модель фильтрации. Предполагается, что основное макроскопическое течение происходит по щелям между блоками. Для описания процесса течения жидкости из блоков к щелям используется уравнение одномерной фильтрации в рамках радиальной и сферической симметричной схем течения.

На основе такой модели решены простейшие модельные задачи, применительно к проблемам гидродинамических исследований скважин

(ГИС).

Литература

1.Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в пористых пластах. М.: Недра, 1984.

2.Басниев К.С., Власов А.М., Кочина И.Н., Максимов В.М. Подземная гидравлика. М.: Недра, 1986.

280

<<< < Предыдущая 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3728 29 30 31 32 33 34 35 36 37 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.05.20152.07 Mб40test_bkh_rastenia.doc
#
17.05.2015265.22 Кб23TETs_kontrolnaya_MU.doc
#
08.05.201922.48 Кб4texty_dlya_1_kursa.docx
#
14.08.201938.03 Кб8Texty_po_anglyskomu.docx
#
17.05.20157.45 Mб34text_Risunok_suslov_sholokhova_prav.pdf
#
17.05.20157.29 Mб40tezisu.pdf
#
17.05.201564.47 Кб202TGP.docx
#
31.08.20191.02 Mб17TGP_IGA.doc
#
17.05.2015109.57 Кб224THE SCHEME OF STYLISTIC ANALYSIS.doc
#
29.08.201942.92 Кб8this was pisdec.docx
#
09.11.201936.45 Кб6tipy_rechi.docx