kniga

всі афінні перетворення залежать від порядку їх виконання. Наприклад, перетворення обертання некомутативні.

Розглянемо два основні методи знаходження матриць складних перетворень:

•метод розкладу (декомпозиції) складного руху об’єкта на n елементарних рухів, що описуються матрицями Ci, і = 1, 2, …, n. Одержаний

ланцюжок із n перетворень еквівалентний одному перетворенню з

n

матрицею С = ∏Ci . В однорідних координатах матриця перетво-

i =1

рення C знаходиться за допомогою тільки операцій множення матриць. Зазначимо, що розклад матриці С на добуток матриць Ci можна здійснити не єдиним способом, тому задача програміста полягає в оптимізації множини елементарних перетворень, що задаються матрицями Ci;

•метод парних точок, що визначає матрицю афінних перетворень за трьома (на площині) та чотирма (в просторі) парами лінійно незалежних точок образу Х та прообразу Х′. За умови, що трійки точок неколінеарні, а четвірки некомпланарні, матриці, які задають ці об’єкти, невироджені, тому завжди можна знайти матриці афінних перетворень.

Найкраща обумовленість матриць досягається при ортогональності систем векторів, що побудовані на вибраних точках образу і прообразу.

Отже, із системи рівнянь X′ = X C знаходимо C = X–1 X′.

Приклад 6. Знайти матрицю перетворення трикутника Р1 Р2 Р3 у трикутник P1′P2′P3′ (рис. 11.10).

y

Рис. 11.10. Перетворення трикутників

221

Однорідні координати вершин трикутника Р1Р2Р3 складають матрицю

Зі співвідношення C = X–1 X′ одержуємо

Тепер можна спробувати підібрати послідовність і параметри елементарних перетворень трикутника Р1Р2Р3 у трикутник P1′P2′P3′ і пере-

конатися, що цей спосіб побудови матриці C у даному випадку складніший.

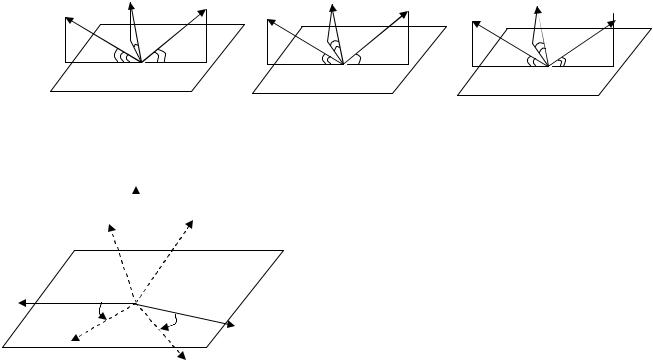
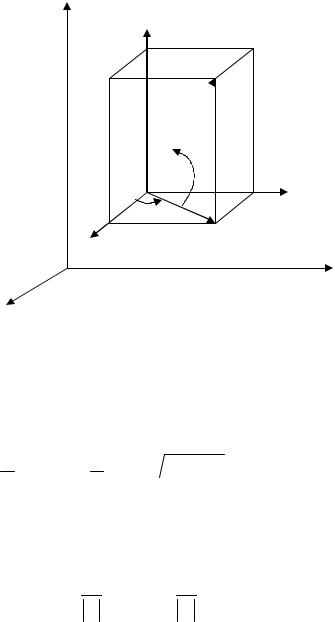
Приклад 7. Розглянути задачу про зміну просторової орієнтації системи координат, як це зображено на рис. 11.11 і на цьому прикладі порівняти алгоритм розкладу та метод парних точок.

Застосуємо спочатку метод розкладу для обчислення матриці складного афінного перетворення на прикладі зміни орієнтації системи координат так, щоб початок координат буде суміщений із точкою O′(m, n, l, 1), а напрям деякої осі, наприклад z, – з напрямком заданого вектора V(a, b, c) (рис. 11.11) (розміщення двох інших осей не регламентується).

Розв’язок задачі досягається за допомогою двох перетворень:

1.Перенесення початку системи координат xyz у точку O′. Це перетворення описується матрицею T(– m, – n, – l) = T –.

2.Поворот системи координат так, щоб вісь z мала напрям вектора V, що виходить уже з початку перенесеної системи координат. Позначимо матрицю цього перетворення A(V), тоді матриця повного перетворення C = T – A(V).

222

у матриці поворотів Ry(–α), Rx(β) та їх множення приводить до громіздкого запису матриці A(V), тому краще множення матриць виконувати програмно.

Застосуємо тепер метод парних точок. Для знаходження матриці A(V) методом парних точок знайдемо в просторі три неколінеарні точки, в які перейдуть кінці ортів x0, y0 , z0 після повороту системи координат. Одна з цих точок, кінець вектора V, є прообразом z0 . У випадку V ≠ z0 виберемо прообрази y0 і x0 на кінцях векторів нормалі N = z0 × V (× – означає векторний добуток) і бінормалі W = N × V. Довжини векторів однакові, тому відсутні спотворення кутів при відображенні, а отже,

де С – матриця перетворення об’єкта. З останнього співвідношення маємо

Якщо об’єкт залишити нерухомим, а перетворювати тільки систему координат, то таке пасивне перетворення задається оберненою матрицею, тобто

Отже, метод парних точок дозволяє знайти матрицю повного перетворення системи координат без розкладу на проміжні перетворення.

Контрольні питання та завдання

1.Які перетворення називаються афінними? Назвіть їх властивості.

2.Що таке однорідні координати? Чому вони застосовуються в КГ?

3.Як задаються афінні перетворення в однорідних координатах?

4.Як побудувати матрицю повороту відносно довільної точки на площині?

5.Випишіть матриці елементарних перетворень в просторі.

6.Які перетворення в просторі є комутативними/некомутативними?

7.Як побудувати матрицю повороту відносно довільної осі?

224

8.Які повороти називаються додатними?

9.Назвіть та порівняйте методи знаходження матриць складних афінних перетворень.

10. Сформулюйте ідею методу парних точок.

Вправи і задачі для самостійного виконання

1.Довести, що перетворення зсуву адитивне, а саме послідовне виконання двох зсувів точки еквівалентне одному зсуву, тобто

T(m1, n1) T(m2, n2)=T(m1+m2, n1+n2).

2.Довести, що два послідовних повороти адитивні, тобто

R(ϕ1+ϕ2)=R(ϕ1) R(ϕ2).

3.Доведіть, що однорідне масштабування і поворот утворюють комутативну групу.

4.Довести, що сумарне масштабування буде мультиплікативним,

тобто якщо виконати масштабування D(a1, b1), а потім D(a2, b2), то результуюче масштабування матиме вигляд D=D(a1a2, b1b2).

5.Побудувати матрицю такої послідовності рухів точки:

a)зсув по осі х на ∆х;

b)поворот відносно попереднього положення точки на кут α;

c)зсув по осі у на ∆у.

6.Довести, що відображення відносно прямої в площині ху, що проходить через початок координат еквівалентно повороту відносно початку координат. Розглянути випадок прямої у = х.

7.Побудувати матрицю загального повороту в 3D-просторі

відносно трьох координатних осей, тобто матрицю Rxyz= Rz(α) Ry(α) Rx(γ). Знайти обернену матрицю цього перетворення.

8.Задано три точки Р1, Р2, Р3 в просторі. Побудувати матрицю перетворення, в результаті якого вектор Р1Р2 буде направлений вздовж осі z, а вектор Р1Р3 буде лежати в площині х = 0.

9.Задана трикутна призма ABCDEF з вершинами A(5;5;0), B(5; 15; 0),

C(15; 5; 0), D(5; 5; 10), E(5; 15; 10), F(15; 5; 10). Обчислити коор-

динати повернутої призми відносно ребра СВ на кут 450.

225

Тема 12. Моделювання проекцій 12. 1. Класифікація проекцій

Для побудови графічних зображень тривимірних об’єктів на площині, екрані дисплея чи папері використовують проекції (від лат. projection – викидати вперед). Проекції відображають тривимірні об’єкти на двовимірну картинну площину (надалі КП), тобто перетворюють точки 3D-простору у 2D-простір. Проекції будуються за допомогою прямих (проекторів), що виходять з центра проектування. Ці прямі проходять через кожну точку об’єкта, перетинаючи КП, і на ній утворюють слід – проекцію об’єкта. Оскільки, проекцією відрізка є відрізок, то для побудови проекції відрізка досить побудувати лише проекції його кінців. Ми розглядатимемо лише проекції на площину (плоскі геометричні проекції), хоча існують проекції на скривлені поверхні – так звані картографічні проекції.

Укомп’ютерній графіці найбільш широко застосовують два класи проекцій: паралельна та центральна (перспективна) проекції.

Увипадку центрального проектування всі прямі виходять з однієї точки – центру проектування, що знаходиться в скінченній точці тривимірного простору (рис. 12.1, б). Центральну проекцію називають ще і перспективною проекцією, або перспективою (від лат. perspicio – ясно бачу). Якщо центр проектування знаходиться на нескінченності, то всі проектори паралельні між собою і в результаті проектування одержу-

ється паралельна проекція (рис. 12.1, а).

S

Рис. 12.1. Паралельна і центральна проекції

До важливих властивостей методу проектування належить ступінь достовірності сприйняття об’єкта спостерігачем за його проекціями, тобто розпізнавання об’єкта за його плоским зображенням. Призначення того чи іншого методу проектування полягає в зменшенні невизначеності найбільш важливих властивостей об’єкта (будь-яка проекція завжди містить у собі похибку, оскільки проектування не є афінним перетворенням, тому воно взагалі не є оберненим). За час розвитку цивілізації знайшли

226

багато різних способів зображення просторових об’єктів на площині.

Зі сказаного вище випливає, що найкращої проекції не існує. В технічних кресленнях для точної передачі розмірів деталей в основному використовуються паралельні проекції. Художниками і архітекторами часто використовуються перспективні види для створення найбільш реалістичного зображення тривимірних об’єктів.

Центральна проекція породжує візуальний ефект, аналогічний до того, який виникає при спостереженні людиною чи фотографуванні, тобто досягається деякий ступінь реалістичності завдяки ефекту перспективного вкорочування. При центральному проектуванні розмір об’єкта зменшується зі збільшенням відстані до центра проекції і відбувається пропорційне спотворення ліній об’єкта, яке залежить від орієнтації лінії та її віддалі від центру проектування. Все це сприяє кращому сприйняттю глибини сцени, однак не зберігає

Рис. 12.2. Точка збігу форму об’єкта.

Центральні проекції довільної сукупності паралельних прямих, не паралельних до проекційної площини, перетинаються в точці збігу (рис. 12.2). Завдяки цій властивості плоскі зображення (проекції) виглядають об’ємно і реалістично.

Кожен із цих двох класів проектування розбивається на підкласи в залежності від взаємного розміщення КП і координатних осей. Центральні проекції умовно можна класифікувати за кількістю точок збігу зображення куба чи паралелепіпеда. Наприклад, проекції каркасних кубів мають одну, дві або три точки збігу і, відповідно, називаються

одноточковими, двоточковими або триточковими перспективами.

Види проектування наведені на рис. 12.3. Побудуємо математичні моделі базових проективних перетворень. Спочатку розглянемо паралельні проекції.

12.2. Ортографічна проекція

Основним типом координатних систем у проективній геометрії є однорідні координати. Використання однорідних координат для задання операцій проектування дозволяє значно полегшити розв’язання задач геометричного моделювання проекцій. А саме операції проектування в однорідних координатах можна подати в матричному вигляді, тобто точ- ка-проекція X′ одержується з точки X за допомогою перетворення X′ = X P, де P – матриця проектування розміром 4 × 4.

227

При ортографічному проектуванні КП збігається з однією із координатних площин або паралельна їй. Якщо проектори паралельні осі z, то точка (x, y, z) проектується в точку (x, y, 0). Матриця ортогонального проектування вздовж осі z має вигляд

Плоскі геометричні проекції

Рис. 12.3. Класифікація проекцій

Аналогічно виписуються матриці ортогонального проектування вздовж двох інших координатних осей

Зауваження 1. Для адекватного відтворення форми об’єкта недостатньо однієї ортогональної проекції, оскільки матриці ортогонального проектування вироджені. Необхідно мати кілька ортогональних проекцій, а саме проекції на площини z = 0, x = 0, y = 0. Вони є видами об’єкта спереду (фронтальний), справа (поздовжній) і зверху (горизонтальний). В технічних кресленнях за основні площини проекцій приймають шість граней куба. Важливо зазначити, що всі шість проекцій можуть бути

228

одержані шляхом комбінування перетворень відображення, повороту, перенесення з наступним ортогональним проектуванням на площину z = 0.

12.3. Аксонометрична проекція

Одна ортографічна проекція не може дати уяви про загальну форму тривимірного об’єкта. Це обмеження можна усунути за допомогою аксонометричних проекцій. Аксонометрична проекція (від грецького axon – вісь, metreo – вимірювати) утворюється маніпулюванням об’єкта за допомогою поворотів так, щоб були видимими принаймні три сусідні грані.

При аксонометричній проекції проектори теж перпендикулярні КП, але вже не паралельні координатних осям. Відповідно до взаємного розміщення КП і координатних осей розрізняють три види аксонометричних проекцій:

–триметрію – нормальний вектор КП утворює з осями координат попарно різні кути (рис. 12.4, а);

–диметрію – два кути між нормаллю КП і осями координат однакові

(рис. 12.4, б);

–ізометрію – всі три кути між нормаллю КП і координатними осями однакові (рис. 12.4, в).

Уцих проекціях можна розглядати також кути між осями координат та самою КП (рис. 12.4).

координат

229

x′y′z′ повернемо навколо осі x′ на кут ϕ у напрямку від z′ до y′ (від’ємний напрям) так, щоб вісь y′ попала в КП (рис. 12.5). Це перетворення здійснює матриця Rx(ϕ). Після цього виконуємо ортогональне проектування вздовж осі z″. В результаті одержуємо матрицю аксоно-

метричного проектування

Триметрична проекція здійснюється довільними поворотами, що виконуються в будь-якому порядку навколо координатних осей із наступним ортографічним проектуванням на КП, тобто ϕ та ψ у матриці А для триметрії є довільними.

На рис. 12.6 зображено триметричні проекції зрізаного куба для різних значень кутів ϕ та ψ. Куб зі зрізаною вершиною задається матрицею Х, де

Координати триметричної проекції зрізаного куба обчислюємо за формулою X′= X A, де A – матриця аксонометричного проектування.

Для диметричної проекції значення кутів ψ та ϕ потрібно відповідним чином підібрати. Для цього розглянемо матрицю X з одиничних ортів координатних осей

230