kniga

8.3.2. В-сплайнові поверхні

Векторне параметричне рівняння елементарного фрагмента бікубічної В-сплайнової поверхні, що задана на масиві точок Pij, i, j = 0, 1, 2, 3

Як і бікубічна поверхня Безьє, елементарна бікубічна В-сплайнова поверхня наслідує багато властивостей елементарної кубічної В-сплай- нової кривої. Об’єднуючи елементарні бікубічні В-сплайни, одержуємо складену В-сплайнову поверхню, для якої на границях двох фрагментів автоматично забезпечується належність класу С2.

Раціональна (елементарна) бікубічна В-сплайнова поверхня за заданим масивом точок Pij, i, j = 0, 1, 2, 3 визначається рівнянням

i=0 j=0

Раціональні В-сплайнові поверхні, які в англомовній літературі називають ще NURBS-поверхнями, широко застосовуються на практиці, наприклад в інженерних системах для моделювання складних поверхонь зі складними межами та дірками, для моделювання людського тіла та тіла тварин, оскільки ними можна описувати довільні геометричні форми.

Тут ми зупинилися лише на деяких способах побудови згладжувальних поверхонь і побачили, наскільки це непроста задача. Реалістичне зображення гладкої поверхні на екрані дисплея – складна задача, вона полягає в розрахунку її форми на основі правильного визначення освітленості видимих точок поверхні, матеріалу поверхні тощо. Спрощена побудова поверхні r = r(u, v) полягає в зображенні її каркаса – сукупності ліній, що передають форму поверхні. Для цього виконується дискретизація неперервних параметрів

u = u0, u1, …, un, v = v0, v1, …, vm

і організація вкладених циклів виведення каркасних ліній r(ui, v) і r(u, vj). Перетин ліній дає комірки трикутної або чотирикутної форми, які апроксимують поверхню.

151

Контрольні питання та завдання

1.Як аналітично можна задавати поверхні? В чому перевага та недоліки параметричної форми?

2.Наведіть приклади параметрично заданих поверхонь.

3.Які поверхні називаються бікубічними? Які вони мають переваги?

4.Як задати білінійну/лінійчасту поверхню?

5.Як задати секторну поверхню?

6.Назвіть властивості інтерполяційного бікубічного сплайна.

7.Як визначається елементарна бікубічна поверхня Безьє?

8.Які властивості має складена бікубічна поверхня Безьє?

9.При яких умовах на граничні контрольні точки складена поверхня Безьє належить класу С1?

10.Як визначається елементарна бікубічна В-сплайнова поверхня?

11.Які властивості має складена бікубічна В-сплайнова поверхня?

12.Що таке NURBS-поверхні?

Вправи і задачі для самостійного виконання

1.Записати рівняння лінійчастої поверхні, що проходить через діагональ куба і бічне ребро, яке не має з діагоналлю спільних точок.

2.Записати в матричній формі рівняння квадратичної поверхні Безьє. Довести, що ця поверхня проходить через крайні кутові точки заданої матриці точок Рij (i, j = 0, 1, 2).

3.Побудувати параметричне рівняння поверхні Безьє за такими контрольними точками

Р00(0,0,0) Р01(1,1,0) Р02(2,1,0) Р03(3,0,0) Р10(0,1,1) Р11(1,2,1) Р12(2,2,1) Р13(3,1,1) Р20(0,1,2) Р21(1,2,2) Р22(2,2,2) Р23(3,1,2) Р30(0,0,3) Р31(1,1,3) Р32(2,1,3) Р33(3,0,3).

4.Розробити алгоритм обчислення вектора нормалі до поверхні Безьє в точці Р(u,v).

5.Записати параметричні рівняння елементарної бікубічної В-сплай- нової поверхні в матричній формі.

6.Побудувати параметричне рівняння В-сплайнової поверхні за контрольними точками з прикладу 3.

7.Узагальнити рівняння кривих Ерміта на поверхні Ерміта.

8.Задати квадратичну поверхню в матричному виді. Як зміниться матриця квадратичної поверхні, якщо над нею здійснити афінні перетворення з матрицею F. Записати координати нормалі до поверхні другого порядку.

152

Тема 9. Основні алгоритми комп’ютерної геометрії

Комп’ютерна геометрія – це сукупність методів і алгоритмів для розв’язування на ЕОМ задач, пов’язаних з різними геометричними побудовами на площині та в просторі.

9.1.Тести орієнтації

9.1.1.Орієнтація нормального вектора

Загальне рівняння прямої має вигляд Ax + By + С = 0. Коефіцієнти A, B утворюють вектор нормалі N = (A, B). Вектор V = (–B, A) задає напрямний вектор прямої, оскільки (N V) = 0.

при русі точки по лінії в напрямку V вектор N направлений вправо від вектора V (вектор V – вліво від N) (рис. 9.1). Тут R(ϕ) є матрицею повороту точки проти годинникової стрілки на кут ϕ.

V

Рис. 9.1. Орієнтація нормалі

N

Іншими словами, якщо рухатись вздовж вектора (А, В), то вектор (В, –А) направлений вправо, тому якщо обходити полігон проти годинникової стрілки, то такі нормалі матимуть зовнішню орієнтацію щодо сторін полігона.

9.1.2. Розміщення точки відносно прямої

Функція f(p) = Ax + By + C, де р = (x, y), дозволяє визначити орієнтацію двох точок a і b відносно прямої Ax + By + C = 0. Так, при f(a) f(b) > 0 точки лежать по один бік від прямої, при f(a) f(b) < 0 – по різні боки від прямої.

Параметричне рівняння прямої, що проходить через точку p0(x0 ,y0) в напрямку вектора V=(Vx,Vy), має вигляд

x = x0 + Vx t, y = y0 + Vy t, або p = p0 + Vt, де p = (x, y).

Параметрична форма зручна для побудови відрізків, при цьому необхідно вказати границі зміни параметра t. Значення t0 ≤ t ≤ t1 визначають відрізок прямої між точками p0 + Vt0 та p0 + Vt1.

Завдяки правій орієнтації вектора N відносно вектора V функція

153

положення точки відносно прямої, що проходить через точку p0 вздовж вектора V (рис. 9.2):

•при f1(p) > 0 точка p лежить справа від прямої (кут між векторами p – p0 і N гострий);

•при f1(q) < 0 точка q лежить зліва (кут між векторами q – p0 і N тупий).

N

9.1.3. Тест напряму обходу трьох точок

Як видно з п. 9.1.2 функція

дозволяє визначити місцезнаходження точки p(x,y) відносно руху по прямій від точки a(ax, ay) до точки b(bx, by):

•при f2(p) > 0 точка p лежить справа від прямої;

•при f2(p) < 0 точка q лежить зліва від прямої. Функція f2(p) може бути визначена і в такий спосіб:

визначає напрям обходу цих точок:

•якщо D > 0, то обхід точок a, b, c здійснюється проти годинникової стрілки;

•якщо D < 0, то обхід точок a, b, c здійснюється за годинниковою стрілкою;

154

• якщо D = 0, то точки a, b, c лежать на прямій лінії.

Зауважимо, що визначник D визначає подвоєну орієнтовану площу трикутника, побудованого на точках a, b, c.

9.2.Тест опуклості полігона

Вопуклому полігоні всі вершини Pi обходяться за годинниковою стрілкою чи проти годинникової стрілки. Щоб реалізувати тест опуклості полігона, достатньо підрахувати значення визначників

Якщо всі Di одного знака, то полігон опуклий, інакше – неопуклий.

9.3. Тести орієнтації точки відносно полігона

Відомі кілька методів перевірки довільної точки на приналежність її полігону. На початковій стадії розв’язування цієї задачі часто застосовують габаритний тест, який іноді ще називають методом оболонок. Цей метод є досить універсальним методом прискорення обчислювальних процесів у задачах комп’ютерної графіки.

9.3.1. Габаритний тест

Суть цього методу полягає в тому, що спочатку аналізуються не самі полігони, а більш прості форми – оболонки, які охоплюють полігони (в нашому випадку – прямокутники). Використання цього методу дозволяє відразу виявити деякі випадки, в яких точка не належить полігону.

Нехай задано полігон P = {P1 P2 ... Pn P1} та точка Q(x, y). Визначимо мінімальні та максимальні координати вершин Pi (i = 1, 2,…, n), тобто мінімальну прямокутну оболонку, якій належить полігон. Позначимо

pxmin = min{pix}, pxmax = max{pix}, pymin = min{piy}, pymax = max{piy}. Тоді умови (x < pxmin) U (x > pxmax) U (y < pymin) U (y > pymax) гарантують неналежність точки Q полігону P.

Повністю габаритний тест задачу розміщення точки відносно полігона не розв’язує, він розпізнає лише точки, які лежать зовні габаритного прямокутника. Якщо точка лежить усередині габаритного прямокутника, то вона не може бути однозначно ідентифікована як зовнішня, внутрішня чи гранична відносно полігона.

Проте, завдяки своїй простоті, габаритний тест застосовується в багатьох алгоритмах для швидкого розпізнавання неперетинних геометричних об’єктів. Для цього навколо кожного об’єкта описують тіло простого вигляду, наприклад прямокутник, паралелепіпед тощо, і якщо ці тіла не перетинаються, то і об’єкти, що містяться в них, теж не

155

перетинаються. Однак слід зауважити, що, якщо тіла перетинаються, то самі об’єкти при цьому не обов’язково перетинаються.

9.3.2. Тест, що визначає орієнтацію точки відносно кожного ребра

Цей алгоритм придатний тільки для опуклих полігонів. У процесі роботи цього алгоритму обходиться границя полігона і проводиться покроковий аналіз взаємного розміщення точки Q і кожного ребра. Оскільки полігон P опуклий, то точка Q лежить усередині полігона тільки тоді, коли вона лежить зліва від кожного ребра при обході полігона проти годинникової стрілки, і справа при обході за годинниковою стрілкою.

9.3.3. Променевий тест

Для розв’язування задачі орієнтації точки Q(x, y) відносно полігона P випускаємо з точки Q у довільному напрямку V промінь p = Q + Vt, t ≥ 0 і обчислюємо кількість точок перетину цього променя з границею полігона. Якщо відкинути випадок, коли промінь проходить через вершини полігона, то розв’язування задачі тривіальне – точка лежить усередині, якщо загальна кількість точок перетину променя з ребрами полігона непарна, і зовні, якщо кількість точок перетину парна.

Зрозуміло, що для довільного полігона завжди можна побудувати промінь, що не проходить через жодну з вершин. Однак побудова такого променя пов’язана з деякими труднощами і, крім цього, перевірку перетину границі полігона з довільним променем провести складніше, ніж, наприклад, із горизонтальним.

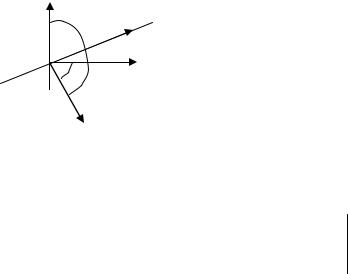
Розглянемо різні випадки перетину горизонтального променя з вершинами полігона (рис. 9.3). У випадку а, коли ребра, що виходять із вершини, лежать по один бік від променя, парність кількості перетинів не змінюється.

У випадку б, коли ребра, що виходять із вершини, лежать по різні сторони від променя, парність кількості перетинів змінюється.

До випадків в і г, коли промінь зустрічається з горизонтальним ребром, такий підхід застосувати не можна.

Отже, у випадку, коли полігон не має горизонтальних ребер, має-

156

мо такий алгоритм. Випускаємо з точки Q горизонтальний промінь і всі ребра полігона перевіряємо на перетин із цим променем. Якщо промінь проходить через вершину (формально перетинає 2 ребра, що виходять із цієї вершини), зараховуємо перетин тільки для тих ребер, для яких ця вершина верхня.

Зауваження 2. У випадках б, г, коли промінь зустрічається з горизонтальним ребром PiPi+1, необхідно перевірити, чи вершини Pi–1 та Pi + 2 лежать по різні боки від променя. Якщо ці вершин лежать по різні боки від променя, то перетин зараховуємо; якщо по один бік, то перетин не зараховуємо.

9.3.4. Кутовий тест

Кутовий тест займає важливе місце в задачах комп’ютерної графіки. Кутовий тест базується на обчисленні й аналізі алгебраїчної суми кутів δi = (Vi, Vi + 1) між суміжними векторами Vi = Pi – Q, що з’єднують точку Q з вершинами Pi при обході полігона P по замкнутому контуру .

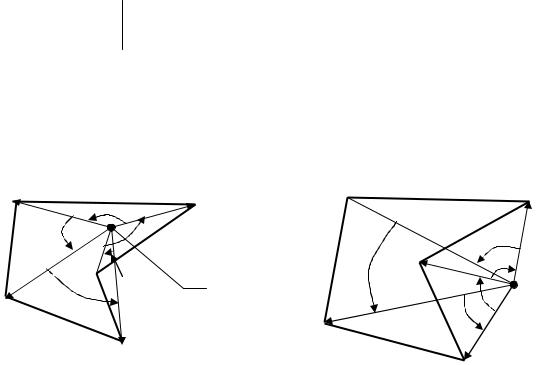
Тест ґрунтується на такому факті: спостерігач, що проглядає вершини полігона з внутрішньої точки Qв, здійснює навколо себе повний оберт (рис. 9.4, а), а з зовнішньої точки Qз – жодного оберту (рис. 9.4, б).

Тоді при всіх ненульових векторах Vi радіанний варіант кутового тесту матиме вигляд

де ang(V, W) – це функція обчислення кута між векторами V і W, як кута найкоротшого повороту від V до W, тобто

Рис. 9.4. Кутовий тест

157

У зв’язку з неминучими обчислювальними похибками, що виникають при знаходженні суми кутів, результат у (9.1) не можна порівнювати ні з нулем, ні з 2π (він завжди буде відрізнятися від цих чисел). Тому для суми кутів пропонують взяти порогове значення π і тоді при будьяких похибках одержимо правильний результат тестування.

Гранична точка полігона розрізняється так:

•якщо при розрахунку векторів матимемо нульовий вектор, то точка збігається з вершиною полігона;

•якщо при розрахунку кутів δi буде одержаний розгорнутий кут з модулем |δi| = π, тоді точка лежить на ребрі. Однак оскільки обчислення здійснюються з плаваючою крапкою, то належність точки Q

ребру PiPi + 1 за допомогою умови |δi| = π на практиці замінюється умовою ||δi| – π| < ε, де ε – експериментально підібрана мінімальна

константа.

Зауважимо, що для того, щоб не проводити розрахунок кутів із високою точністю, існують відповідні модифікації кутового тесту.

Значно спрощується тест орієнтації точки Q відносно трикутника P1 P2 P3 [14]. Для цього достатньо записати розклад вектора QP1 за век-

де V = p2 – p1, W = p3 – p1.

Далі систему (9.2) необхідно розв’язати відносно τ, t або скористатись методом Грамма і скласти нову систему двох лінійних рівнянь зі скалярних добутків

(q – p1)V = t(V V) + τ (W V),

(q – p1)W = t(V W) + τ (W W)

та знайти розв’язок

Матриця, що фігурує в (9.3), невироджена, оскільки визначник

|V|2 |W|2 – (V W)2 = |V|2 |W|2 sin2 ( (V, W)) > 0

і дорівнює нулю лише при колінеарності вершин трикутника P1 P2 P3 .

158

9.4.Тести перетину

9.4.1.Тест перетину прямої з полігоном

Пряма перетинає полігон, якщо існує хоча б одна пара вершин полігона, що лежать по різні боки від цієї прямої (рис. 9.5).

Зазначимо, що необхідно порівнювати розміщення відносно прямої лінії f(p) = 0 не тільки суміжні вершини Pi та Pi + 1 полігона, а й решту пар вершин {Pi, Pj}, оскільки пряма може перетинати полігон тільки у вершинах (рис. 9.5, б). Різні знаки чисел f(pi) і f(pj) дають умову перетину прямої f(p) = 0 з полігоном P.

зувати цю задачу прямим шляхом, то при великих n (наприклад, n – число порядку тисяч) кількість операцій порівнянь недопустимо велика (пропорційна n2). За допомогою спеціальних прийомів цю кількість операцій можна зменшити. Розглянемо деякі з цих алгоритмів.

¾У зовнішньому циклі i = 1, 2, …, n обчислюємо значення si = f(pi). У внутрішньому циклі j = 1, 2, …, i – 1, i > 1 аналізуємо знак добутку

si sj (зауважимо, що sj = f(pj) для j < i вже обчислено). При si sj < 0 тест негайно завершується, повертаючи ознаку перетину прямої з полігоном, інакше після нормального завершення зовнішнього циклу одержуємо або відсутність перетину, або дотик прямої з полігоном.

¾У циклі по i = 1, 2, …, n обчислимо значення si = f(pi) і виконаємо сортування вектора s. Результат тестування задається числом res =

sign(s1 sn). При res = –1 крайні елементи мають різні знаки, що означає перетин із полігоном, при res = 0 пряма дотикається до полігона, при res = 1 відсутній перетин прямої з полігоном. Недолік

цього методу – наявність операції сортування, в якій кількість операцій порівняння оцінюється величиною nlgn, що менше n2.

159

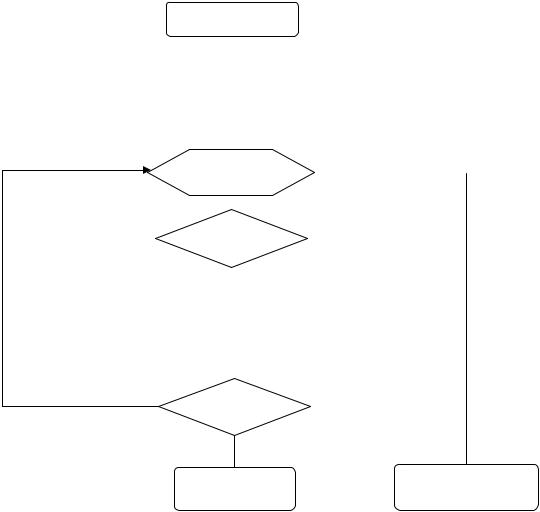
¾Ще один варіант алгоритму тесту перетину прямої з многокутником використовує три прапорці, що сигналізують про розміщення вершини зліва (прапорець l), справа (прапорець r) і точно на прямій (прапорець е). На початку всі прапорці виставляємо в нуль. У циклі

по i = 1, 2, …, n обчислюємо значення s = f(pi) і виставляємо в 1 один із прапорців: l = 1, якщо s < 0; е = 1, якщо s = 0; r = 1, якщо s > 0. З допомогою умови l r ≠ 0 перевіряємо наявність пари вершин полігона, що знаходяться по різні боки від прямої. Якщо ця умова виконується, то тест негайно завершується, повертаючи 1 – ознаку перетину прямої з полігоном. Після нормального закінчення циклу обходу вершин алгоритм повертає значення e–1, яке дорівнює 0, якщо пряма дотикається до полігона, та –1, якщо відсутній перетин прямої з цим полігоном. Блок-схему цього алгоритму [21] поданонарис. 9.6.

Рис. 9.6. Блок-схема тесту перетину прямої з полігоном

160