kniga

Згадаємо векторно-параметричне рівняння відрізка ab

V(t) = a + (b – a)t, t [0, 1]. (9.6)

Оскільки многокутник опуклий, то може бути дві точки перетину відрізка ab із вікном P і нам необхідно знайти два значення параметра t, що відповідають початковій і кінцевій точкам видимої частини відрізка.

З умови належності точки V(t) границі вікна, тобто з умови qi = 0, враховуючи (9.5) та (9.6), маємо

(ni (a + (b – a)t – Pi))) = 0,

або

(ni (a – Pi)) + (ni (b – a)t) = 0.

Звідки

(9.7)

Алгоритм Кіруса-Бека має наступний вигляд.

Шукані значення параметрів t0, t1 точок перетину відрізка з вікном ініціалізуємо значеннями 0, 1, що відповідають початку і кінцю відрізка ab.

В циклі по i для кожної сторони вікна відсікання обчислюємо значення скалярних добутків

ri = (ni (b – a)).

Якщо ri = 0, то відрізок ab або вироджується в точку, або паралельний i-й стороні вікна. При цьому проаналізуємо значення qi = (ni (a – Pi)). Якщо qi < 0, то відрізок знаходиться зовні вікна і відсікання закінчено, інакше переходимо до наступної сторони вікна.

Якщо ri ≠ 0, то за формулою (9.7) обчисляємо значення t для точки перетину відрізка ab з i-ю границею вікна. Оскільки точки відрізка ab відповідають значенням t [0, 1], то t [0, 1] відкидаємо.

При ri < 0 лінія ab направлена з внутрішньої сторони і-граничної лінії на зовнішню і знайдені значення t визначатимуть кінцеву точку видимої частини відрізка ab. В цьому випадку визначається min t серед всіх одержаних t (рис. 9.18). Воно дає значення t1 для кінцевої точки шуканого відрізка

Якщо поточне значення t1 стане меншим за t0, то відрізок ab відкидається, оскільки не виконується умова t0 ≤ t1.

При ri > 0 лінія ab направлена із зовнішньої сторони граничної лінії на внутрішню, тому знайдені значення t визначатимуть початкову точку

171

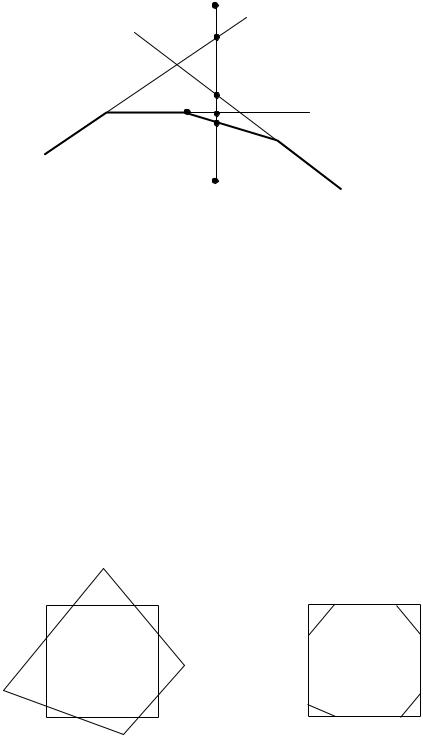
видимої частини відрізка ab. В цьому випадку визначається max t серед всіх одержаних t. Воно дає значення t0 для початкової точки видимої частини відрізка

Якщо поточне значення t0 стане більшим за t1, то відрізок відсікається.

Рис. 9.18. Визначення кінцевої точки V(t1)

На заключному етапі алгоритму значення t0, t1 використовуються для знаходження координат точок перетину відрізка ab з вікном P, тобто для побудови видимої частини відрізка.

При цьому, якщо t0 = 0, то початкова точка залишається та сама й обчислення V(t0) не потрібні. Аналогічно при t1 = 1 кінцева точка – b. Обчислення V(t1) теж не потрібні.

9.6.3. Відсікання полігонів. Алгоритм Вейлера-Азертона

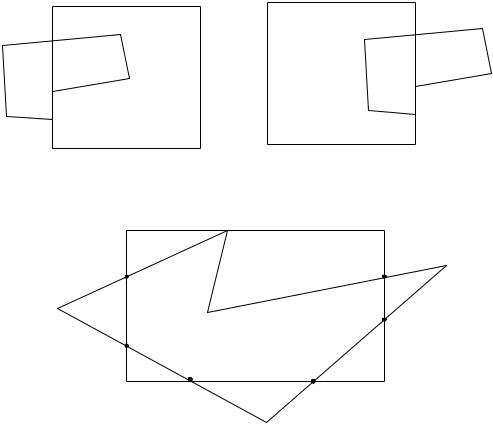
Многокутник можна розглядати як сукупність відрізків, але в цьому випадку при відсіканні вихідна фігура може перетворитися просто в набір відрізків (рис. 9.19). Тому необхідно мати ефективні алгоритми відсікання многокутників. До таких алгоритмів належать алгоритм Сазерленда-Ходжмена для відсікання опуклих многокутників та більш сильний алгоритм Вейлера-Азертона для відсікання довільних областей.

Рис. 9.19. Відсікання вікном ребер многокутника

172

На відміну від інших алгоритмів відсікання, алгоритм ВейлераАзертона дозволяє відсікати довільний неопуклий многокутник з дірками іншим неопуклим многокутником з дірками, причому можливе як зовнішнє, так і внутрішнє відсікання. Розглянемо його.

Кожний з многокутників у цьому алгоритмі задається циклічним списком вершин, причому вершини зовнішньої границі кожного многокутника обходяться за годинниковою стрілкою, а внутрішня границя (дірки) – проти годинникової стрілки так, щоб внутрішня область многокутників завжди залишалась справа від границі.

Границі многокутника, що відсікається, і вікна можуть перетинатися або не перетинатися. Якщо вони перетинаються, то виникають точки перетину ребер двох типів:

–вхідні точки, коли орієнтовані ребра многокутника, що відсікається, входять у вікно;

–вихідні точки, коли ребра многокутника, що відсікається, виходять із внутрішньої сторони вікна на зовнішню.

Точки перетину заносяться в циклічні списки вершин двох многокутників так, щоб не порушити правила обходу границі многокутників, тобто якщо точка перетину Ik знаходиться на ребрі, що з’єднує вершини Рi, Рi+1, то послідовність Рi Рi+ 1 перетворюється в послідовність Pi Ik Pi + 1.

Алгоритм починається з точки перетину вхідного типу. Далі він простежує модифікований список вершин (границю многокутника) доти, поки не буде знайдено наступну точку перетину (вхідну чи вихідну). В цій точці відбувається поворот „направо”, тобто переключення на інший список в цю саму точку перетину. Далі в цьому списку знаходиться наступна точка перетину і відбувається переключення на перший список (поворот „наліво”) і т.д., поки не зустрінеться початкова вхідна точка.

Загальна схема алгоритма Вейлера-Азертона має такий вигляд:

–побудувати циклічні списки вершин многокутника, що відсікається та вікна, згідно з наведеним вище правилом обходу;

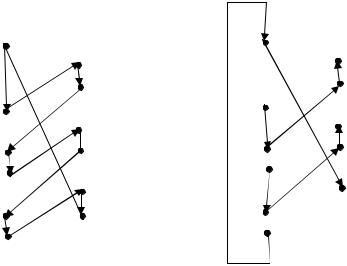
–відшукати всі точки перетину вікна і многокутника (при цих обчисленнях дотикання не вважається перетином (рис. 9.20, 9.21));

Рис. 9.20. Випадки дотикання (не вважається перетином): а – дотикання ребром; б – дотикання вершиною

173

Для пошуку зовнішнього відсікання алгоритм необхідно починати з вихідної точки перетину, при цьому вершини в списку вершин вікна треба переглядати у зворотному порядку.

Для наочності наведемо приклад. Нехай вікном ABCD відсікається многокутник P1P2P3P3P4P5 (рис. 9.22).

Для внутрішнього відсікання циклічні списки вершин і порядок роботи алгоритма зображені на рис. 9.23. Як вхідна вибрана точка I1. Пройдені точки формують результат I1P2P3I2I3I4I5I6I1.

Рис. 9.23. Схема алгоритму Вейлера-Азертона: а – внутрішнє відсікання; б – зовнішнє відсікання

Для виконання зовнішнього відсікання як початкову беремо вихідну точку перетину, наприклад I2. Далі діємо згідно з алгоритмом, проходячи вершини вікна знизу вверх.

В результаті одержуємо три частини многокутника: I2P4I3I2, I4P5I5I4, I6P1I1I6, що відсікаються вікном.

9.7. Побудова опуклої оболонки масиву точок

Припустимо, що на площині задано масив точок P = {P1, P2, …, Pn} з координатами Pi(xi, yi), i = 1, 2, …, n , n ≥ 2.

Опукла полігональна оболонка масиву точок є об’єднанням усіх полігонів, побудованих на точках цього масиву як на вершинах. Її можна зобразити як опуклий полігон мінімальної площі, що покриває всі точки масиву (зазначимо, що не всі точки з масиву P є вершинами опуклої оболонки). Існує багато різних алгоритмів для пошуку опуклої оболонки. Наведемо деякі з них.

175

9.7.1. Метод загортання подарунка

Спочатку обираємо напрям обходу точок масиву (наприклад, додатний) та точку, яка точно є вершиною границі опуклої оболонки. За таку точку можна взяти точку Pm із мінімальною ординатою ym. Якщо таких точок декілька, то оберемо найлівішу з них, тобто точку з мінімальною абсцисою xm. Шляхом обміну P1 ↔ Pm поставимо знайдену точку на початок масиву, а її копію добавимо в кінець масиву як точку Pn+1 для перевірки замикання оболонки.

Задаємо початковий напрям вектора охоплення V вздовж осі x та індекс вершини оболонки k = 1. Далі організовуємо зовнішній цикл пошуку вершин оболонки і накопичення їх по порядку в масиві Р. У внутрішньому циклі по i від k+1 до n+1 для кожної точки Pi обчислюється вектор пробного напрямку W = Pi – Pk. При ненульовій довжині цього вектора r = |W| ≠ 0 (така перевірка дозволяє відкинути крайні точки) знаходимо

176

9.7.2. Метод обходу Грехема

Розглянемо ще один алгоритм побудови опуклої оболонки – метод обходу Грехема. У цьому методі опукла оболонка скінченного набору точок S знаходиться у два етапи.

На першому кроці вибираємо деяку екстремальну точку Pе S і сортуємо решту точок відповідно до кута нахилу променя, який проведений у ці точки з точки Pе, до горизонталі. Якщо дві точки мають однаковий полярний кут, то точка, яка розміщена ближче до Pе, ставиться у відсортованому масиві раніше. Щоб здійснити це впорядкування, необхідно обчислити відстань або порівняти суму абсолютних значень координат. Як екстремальну вибираємо точку з мінімальною y-ко- ординатою і міняємо її місцем з точкою P1.

На другому кроці алгоритму виконуємо покрокову обробку відсортованих точок, формуючи нову послідовність тимчасових точок (ребер), які зрештою утворять шукану опуклу оболонку. Попереднє сортування точок спрощує виконання побудови опуклої оболонки.

Для розв’язування питання про те, яка саме точка повинна бути включена в границю опуклої оболонки, використовується той факт, що при обході границі опуклої оболонки проти годинникової стрілки кожна вершина повинна відповідати повороту вліво.

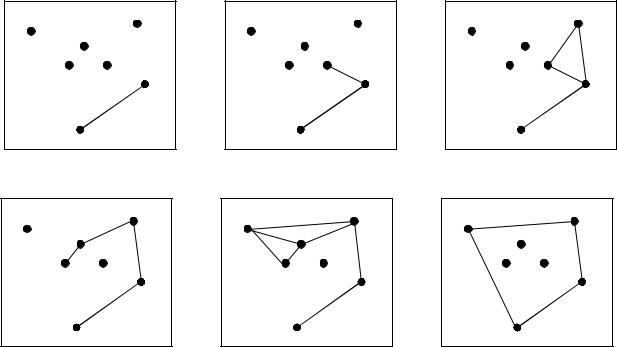
Якщо для точки Pi обхід Pi – 1 Pi Pi + 1 не відповідає повороту вліво, то точка Pi вилучається з опуклої оболонки, а далі потрібно перейти на перевірку повороту вліво обходу Pi – 2 Pi – 1 Pi + 1. Якщо і цей поворот не є поворотом вліво, то вилучаємо точку Pi – 1 , хоча раніше вона була включена в тимчасову послідовність, тобто поворот Pi–2 Pi– 1 Pi був лівим. Цей процес продовжуємо доти, поки не знайдемо лівий поворот, тобто поточна опукла оболонка будується на основі уже оброблених точок. На рис. 9.25 зображено процес роботи алгоритму Грехема.

Розглянемо обробку точки P5 (рис. 9.25, д). Оскільки обхід P4 P5 P6 не є лівим, то P5 вилучається з поточної оболонки. Далі перевіряємо обхід P3 P4 P6 – він теж не є лівим. Тому і P4 вилучаємо з поточної оболонки.

Ситуація змінюється при розгляді точки P3. Тут обхід P1 P3 P6 лівий, тому в поточній оболонці залишаємо точку P3 та переходимо до обробки наступної точки P6, тобто розглядаємо поворот P3 P6 P0 .

Метод обходу Грехема вимагає O(nlgn) арифметичних операцій.

177

Рис. 9.25. Робота алгоритму обходу Грехема (точки Рi, i = 0, 1,…, 6 вже заздалегідь відсортовані за полярним кутом)

Зауваження 3. До недоліків алгоритму Грехема можна віднести той факт, що він не допускає розбиття вихідної задачі на підзадачі для паралельної обробки даних. Тому розроблені алгоритми побудови опуклої оболонки, що базуються на розбитті вихідної множини точок на дві підмножини і об’єднанні двох ламаних в випуклу оболонку.

Зауваження 4. В алгоритмі Грехема використовуються тригонометричні функції, а їх обчислення вимагають великих обчислювальних затрат в часі. Тому для швидкодіючих алгоритмів необхідно уникати цих обчислень. Для цього вчиняють так: серед n точок знаходять найбільш ліву і найбільш праву точки, які вочевидь є вершинами опуклої оболонки. Пряма, що проходить через ці дві точки, ділить дану множину на дві частини. Обидві ці частини породжують дві частини опуклої оболонки, причому вони є монотонними ламаними відносно осі х. Тому, окремо відсортувавши точки за значенням абсциси, виконуємо обхід Грехема.

Зауваження 5. Алгоритм Грехема не відкритий, оскільки перед початком роботи алгоритму потрібно знати усі n точок. Однак у деяких випадках потрібно мати алгоритм, який буде змінювати опуклу оболонку в міру надходження нових точок. Такі алгоритми розроблені і називаються динамічними.

178

9.8. Тріангуляція полігонів

Широко розповсюдженою задачею обчислювальної геометрії є задача тріангуляції полігонів. Тріангуляцією називається операція розрізування простих полігонів на трикутники за допомогою неперетинних внутрішніх діагоналей. Вона часто використовується для зведення роз- в’язування різних задач (перетину, відсікання, усунення невидимих граней тощо) в області, що має складну конфігурацію, до сукупності задач, що розв’язуються в області трикутника, оскільки трикутник є простішою областю і завжди опуклим, а в цьому випадку задачі розв’язуються значно простіше. Наприклад, для визначення належності точки неопуклому полігону можна здійснити його тріангуляцію й подальшу перевірку належності точки хоча б одному трикутнику.

При аналізі складних криволінійних поверхонь поверхню можна апроксимувати сіткою трикутників, для яких значно простіше розв’я- зуються задачі візуалізації, зокрема зафарбовування точок трикутної грані в однорідний колір завдяки її планарності. Розрізування полігона на трикутники може бути ручним і алгоритмічним. Ручне розрізування можна застосувати до апріорі відомого полігона. Якщо полігон обчислюється в процесі роботи програми та заздалегідь не відома його конфігурація, то необхідно використовувати алгоритми тріангуляції.

9.8.1. Тріангуляція опуклих полігонів

Задача тріангуляції опуклого n-полігона розв’язується просто. Для цього досить провести n – 3 діагоналей P1P3, P1P4, …, P1Pn – 1, у результаті чого одержуємо n – 2 трикутники (рис. 9.26, а). Доведено, що цей факт правильний для будь-якого n-полігона, оскільки в будь-якому полігоні можна провести n – 3 діагоналі.

Рис.9.26. Тріангуляція опуклих полігонів

Опуклий полігон можна розрізати на на n трикутників ще й в інший спосіб (рис. 9.26, б):

CP1P2 U CP2P3 U … U CPn P1,

179

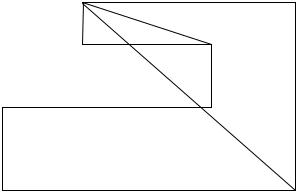
ввівши додаткову вершиною C, яку можна обчислити як геометричний центр полігона

C = 1 ∑n Рi .

n i =1

В цьому випадку одержується більше трикутників і вони мають менш витягнуту форму, ніж при розрізуванні діагоналями.

9.8.2. Тріангуляція неопуклих полігонів

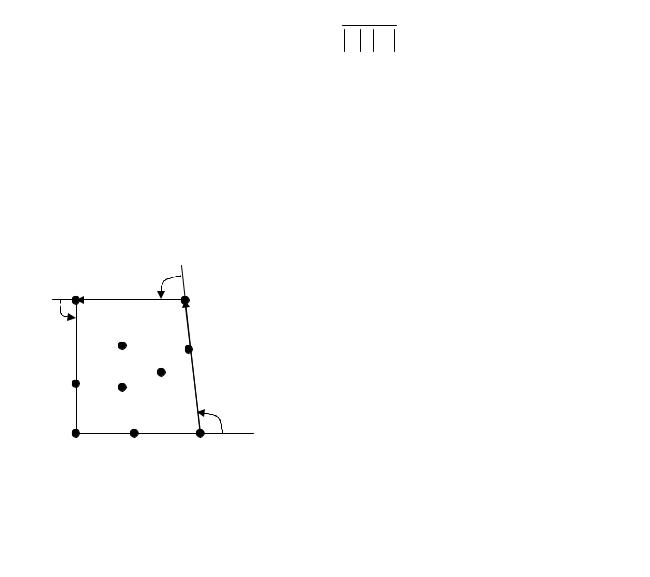
Для тріангуляції неопуклого полігона спочатку шукають вершину, з якої можна провести відсікаючу діагональ. Для цього підходить не кожна опукла вершина (наприклад, точка P2 на рис. 9.28). Діагональ P1P3 не належить внутрішній частині полігона P. Діагональ називається внутрішньою, якщо вона цілком лежить усередині полігона (відомо, що у довільному простому многокутнику з n ≥ 4 вершинами можна провести внутрішню діагональ).

Діагональ опуклої вершини Pi може бути лише кандидатом для відсікаючої діагоналі. Питання вибору діагоналі можна розв’язати, якщо врахувати довжину діагоналей. Для цього здійснюють обхід полігона проти годинникової стрілки по всіх опуклих вершинах полігона, починаючи з точки P1. Нагадаємо, що при цьому вершина Pi опукла, якщо

Далі вибирають найкоротшу діагональ Pi – 1 Pi +1 серед діагоналей опуклих вершин Pi. Ця діагональ буде відсікати від полігона трикутник Pi – 1 Pi Pi+1. Потім цю процеду-

меншу довжину має діагональ P3P5, тому відтинаємо трикутник P3 P4 P5. Залишиться полігон

180