kniga

10.4.4. Фрактали Ньютона

Для знаходження комплексних коренів нелінійного рівняння f(z) = 0

Якщо вдало підібрати z0, то за допомогою попередньої формули одер-

Підбираючи початкове значення z0, можна знаходити n a . Крім цього, відомо, що рівняння zn = a має n коренів, розміщених на колі радіусом

Корені n a є стійкими нерухомими точками відображення (10.7). Основна проблема в застосуванні методу Ньютона пов’язана з вибо-

ром початкового наближення. Для цього потрібно вказати області притягування нерухомих точок відображення (10.7). Границя областей притягування різних коренів має фрактальну структуру. Побудова фракталів Ньютона на комп’ютері аналогічна побудові фракталів Мандельброта. Наприклад, при a = 1 вибираємо множину початкових точок z0 [–2, 2] × [–2, 2]. Далі для кожного пікселя екрана підбираємо значення z0 і перевіряємо, чи орбіта, що виходить з точки z0, наближається до нерухомих точок (коренів рівняння). Умовою припинення циклу ітерацій є наближення значень |zn – 1| до нуля (наприклад, |zn – 1| < 0,01) або при

досягненні k = Kmax.

При a = 1, n = 3 формули (10.7) набувають вигляду

Піксель, що відповідає значенню (xk, yk), зафарбовуємо в колір k mod 256, де k – номер ітерації, починаючи з якого, виконується нерівність

| zkn – 1| < 0,01.

201

Отже, моделювання ітераційних процесів обчислювальної математики практично довело фрактальність областей збіжності ітерацій до коренів нелінійних рівнянь.

Можна придумати багато інших ітераційних процедур вигляду

zк + 1 = F(zк, c), к = 0, 1, 2, …,

що породжують різноманітні фрактальні зображення.

10.5. Застосування фракталів

За останні 20 років фрактали стали досить популярними. Вони знаходять широке застосування в багатьох областях КГ, наприклад у ком- п’ютерному дизайні. Фрактальна геометрія використовується при моделюванні природніх явищ, при вивченні нелінійних динамічних систем, при обробці та класифікації сигналів складної форми, при аналізі коливання курсу валют. Фрактали застосовуються у фізиці твердого тіла, електроніці, фізиці суцільних середовищ (так з’явилася теорія фрактальних тріщин).

Структури, що схожі на фрактали, можна знайти в навколишньому середовищі: контури хмар, контури морських берегів, турбулентні потоки в рідинах, тріщини в породах, зображення структур деяких речовин, отримані під мікроскопом тощо. Фрактали описують природні форми більш витончено і точніше, ніж об’єкти евклідової геометрії.

Останнім часом методи ітеративних функцій застосовуються не тільки для створення зображень, але й для ефективного стиску графічних зображень при записі у файли. Ідея фрактального стиску полягає в тому, що в графічному зображенні знаходять подібні області і зберігають у файлі тільки коефіцієнти перетворення подібності. При цьому необхідно розв’язувати обернену задачу: для зображення підібрати коефіцієнти перетворення, але проблема полягає в тому, що досить важко знайти ці перетворення.

Графічні зображення кодуються кількома простими перетвореннями, тобто коефіцієнтами цих перетворень. Наприклад, якщо деяке зображення закодуємо двома афінними перетвореннями вигляду

x′ = ax + by + c, y′ = dx + ey + f,

то ми його можемо однозначно визначити за допомогою 12 коефіцієнтів. Такі методи стиску графічної інформації називають методами фрактального стиску. Ці алгоритми дозволяють стискати інформацію в сотні

разів без помітного погіршення зображення.

202

Контрольні питання та завдання

1.Дайте означення фрактала за Мандельбротом.

2.Які фрактали називаються конструктивними? Наведіть приклади.

3.Які фрактали називаються динамічними? Наведіть приклади.

4.Опишіть принципи побудови геометричних фракталів, зокрема фракталів Коха, Леві, Мінковського.

5.Опишіть структуру зіркових фракталів.

6.Які афінні перетворення використовуються при побудові зіркових фракталів?

7.Запишіть алгоритм побудови фрактала „гілка папороті”.

8.Як описуються фрактали Жуліа та Мандельброта? Яка між ними різниця? Як їх побудувати?

9.Опишіть процес побудови фракталів Ньютона на комп’ютері.

10.За якою ознакою зупиняють обчислювальний процес при побудові фракталів Ньютона?

11.Назвіть області застосування фракталів.

12.Як на вашу думку можна будувати стохастичні фрактали?

Вправи і задачі для самостійного виконання

1.Модифікувати алгоритм побудови фрактала „гілка папороті” на випадок урахування товщини стовбура.

2.Розробити алгоритм побудови різнокольорового фрактала „гілка папороті”.

3.Написати програму побудови фрактала, який одержується за ітераційною формулою zк + 1 = i( z к2 + 1), к = 0, 1, 2, … .

4.Розробити алгоритм побудови зіркового фрактала, який складається з квадрата та гірлянди з чотирьох менших квадратів у трьох вільних кінцях яких містяться ще менші квадрати і т.д. Сформулюйте правило довжин відрізків ламаної для такого фрактала.

5.Придумайте одновимірні комплексні відображення, які на вашу думку можуть породити цікаві динамічні фрактали.

6.Побудувати систему ітеративних функцій (IFS) для трикутника Серпінського.

7.Написати фрагмент програми, яка для систем ітеративних функцій буде випадковим чином вибирати функцію із списку n функцій.

8.Побудуйте систему ітеративних функцій (IFS) для трикутника Серпінського.

9.Побудувати фрактали Жуліа та Мандельброта у випадку коли z – гіперкомплексне число.

203

Тема 11. Моделювання 2D/3D-перетворень

Конструювання та виконання різноманітних дій з геометричними об’єктами є центральною задачею в графічних системах. Тому вибір математичних методів і алгоритмів для її реалізації суттєво впливає на ефективність графічної системи. У сучасній комп’ютерній графіці досить широко використовується метод координат, оскільки графічне зображення складається з пікселів, які задаються координатами. Крім цього, координати використовуються для опису розміщення об’єктів та для створення зображень шляхом перетворень з однієї системи кординат в іншу. При цьому використовуються двовимірні та тривимірні системи координат.

Укомп’ютерній графіці все, що стосується двовимірного випадку, позначають символом 2D (2-dimension), а тривимірного – 3D (3-dimen- sion).

На координатному методі базується й аналітична геометрія, яку можна вважати фундаментом КГ. Підходи та ідеї геометрії паралельно з постійно розширюючими можливостями комп’ютерних технічних засобів є істотним джерелом розвитку КГ та її ефективного використання на практиці. Інколи навіть простіші геометричні знання допомагають у розв’язанні складних графічних задач. Усі маніпуляції над графічними зображеннями (перенесення, поворот, масштабування тощо) можна виконати з допомогою відповідного математичного апарату геометрії. Цей апарат повинен бути адаптований до задач комп’ютерної графіки. Тому для засвоєння методів КГ важливе вивчення методів перетворення координат. У цьому розділі описано геометричні перетворення координат на площині та в просторі.

11.1.Афінні перетворення на площині

Упрямокутній системі координат на площині точка M визначається своїми координатами – впорядкованою парою чисел (x, y) або матрицею

розміром 1 × 2.

Якщо на площині ввести ще одну систему координат, то точці M(x, y) ставиться у відповідність нова пара чисел (x′, y′). Перехід від однієї системи координат на площині до іншої задається формулами

x′ = ax + by + m, y′ = cx + dy + n, (11.1)

де a, b, c, d, m, n – довільні числа, ∆ = ad – bc ≠ 0.

Перетворення, що задаються формулами (11.1), називаються афінними. Афінні перетворення мають такі властивості:

•n-вимірний об’єкт відображається в n-вимірний, точка – в точку, лінія – в лінію, поверхня – в поверхню;

204

•зберігається паралельність ліній і площин;

•зберігаються пропорції паралельних об’єктів (довжин відрізків на

паралельних прямих і площ на паралельних площинах).

Ці властивості дозволяють будувати прообрази полігонів на площині й поліедрів у просторі за скінченним набором точок – їх вершин. Зазначимо, що для однозначного визначення коефіцієнтів перетворення (11.1) необхідно задати три пари неколінеарних точок, які повинні відображатися одна в одну перетворенням (11.1).

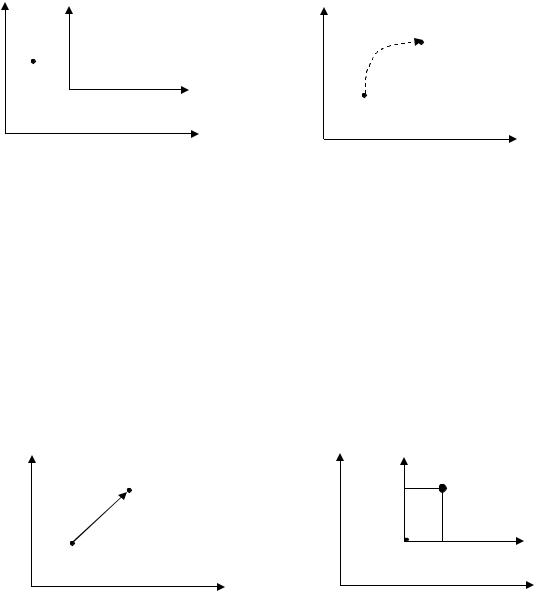
Формули (11.1) можна розглядати двояко: або зберігається точка, а змінюється система координат (рис. 11.1, а), або змінюється точка, а система координат зберігається (рис. 11.1,б). В останньому випадку формули (11.1) задають відображення точки M(x, y) у точку M′(x′, y′).

В афінних перетвореннях площини особливу роль відіграють декілька важливих окремих випадків, а саме

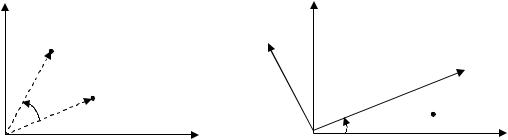
•паралельний зсув координат точки на вектор (m, n) в даній системі координат (рис. 11.2, а) визначається за формулами:

•зсув системи координат на вектор (m, n) (рис. 11.2, б) задається формулами

x′ = x – m, y′ = y – n.

Рис. 11.2. Перетворення зсуву

205

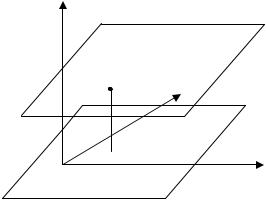
•поворот точки відносно початку координат на кут ϕ проти годинникової стрілки (рис. 11.3, а) описується формулами

•поворот системи координат на кут ϕ проти годинникової стрілки (рис. 11.3, б) задається формулами

x′ = xcosϕ + ysinϕ , y′ = –xsinϕ + ycosϕ ;

•розтяг/стиск вздовж координатних осей можна записати формулами

Якщо в (11.4) a = d, то маємо пропорційне масштабування, якщо a ≠ d, то масштабування – непропорційне. При a = d > 1 відбувається збільшення зображення, при a = d < 1 – рівномірний стиск. При a = 1, d = –1 одержуємо дзеркальне відображення відносно осі x, при a = –1, d = 1 – дзеркальне відображення відносно осі y.

В аналітичній геометрії доведено, що довільне афінне відображення (11.1) можна задати за допомогою композиції елементарних відображень (11.2) – (11.4).

Рис. 11.3. Перетворення повороту

Для ефективного використання формул (11.2) – (11.4) у задачах КГ переходять до матричного запису цих формул. Наприклад, для перетворення (11.3) маємо:

Тобто перетворення повороту відносно початку координат у додатному напрямку на довільний кут ϕ задається матрицею

Зауважимо, що повороти вважаються додатними, якщо вони здійснюються проти годинникової стрілки.

206

У матричному вигляді можна записати і перетворення масштабування

Матричний запис геометричних перетворень дає можливість здійснювати обернені перетворення, тобто точку (об’єкт) X′ можна легко повернути в початковий стан X. Наприклад, для повороту обернене

Зауважимо, що обернена матриця R–1 водночас є транспонованою до R (такі матриці називаються ортогональними). Цей факт є досить важливим для швидкодії алгоритмів.

Але, на жаль, паралельне перенесення (11.2) не вдається задати перетворенням вигляду

тим більше, не можна подати довільні сумарні афінні перетворення в матричній формі. Щоб задати перетворення (11.1) у матричному вигляді (11.6), необхідно перейти до однорідних координат.

Однорідні координати вводяться штучно: довільній точці M(x, y) площини ставиться у відповідність точка M′(x, y, 1) або M′(hx, hy, h), h ≠ 0 в просторі. Фіктивна z-координата має значення скалярної константи, найчастіше h=1.

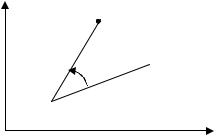
Вектор із координатами (hx, hy, h) є напрямним вектором прямої, що проходить через точки O(0, 0, 0) і M′(x, y, 1). Ця пряма перетинає площину z = 1 в точці (x, y, 1), яка однозначно визначає точку (x, y) координатної площини Оxy (рис. 11.4).

z

M′(x, y, 1) y

Рис. 11.4. Однорідні координати

M(x, y)

x

Отже, між однорідними координатами (x, y, 1) точки та її декартовими координатами (x, y) існує взаємно однозначна відповідність.

207

Еквівалентність векторів

(hx, hy, h) ~ (x, y, 1)

означає, що вони мають однакові декартові координати.

Для зведення однорідного вектора до декартової форми необхідно помножити всі координати на 1h , тобто поділити на h.

Над однорідними координатами за спеціальними формулами можна проводити операції, і тільки на останньому етапі перед виведенням зображення на екран необхідно перейти до декартових координат.

Основні операції з однорідними координатами:

• додавання/віднімання

• множення вектора на скаляр

Застосування однорідних координат дає багато зручностей при роз- в’язуванні графічних задач, наприклад для пристроїв, що працюють з цілими координатами для точки M(0,5; 0,1) можна вибрати h = 10 і мати справу з однорідними цілими координатами M′(5; 1; 10).

Крім цього, однорідні координати дозволяють записувати безмежно віддалені точки простору, уникаючи переповнення розрядної сітки ЕОМ, завдяки нормалізації чисел. За допомогою однорідних координат можна оперувати точкою, що знаходиться в нескінченності.

Але основною метою введення в розгляд однорідних координат у КГ є зручність при заданні геометричних перетворень у матричній формі.

За допомогою однорідних координат і матриць третього порядку можна описати довільне афінне перетворення. Формули (11.1) можна подати в матричній формі (11.6), тобто

де елементи a, b, c, d визначають масштабування і поворот, а m, n – сумарний зсув. Отже, всі перетворення зсуву, масштабування, повороту відносно початку координат в однорідних координатах мають однакову форму – це добуток вектора вихідних координат на матрицю перетворення.

208

Випишемо матриці основних елементарних перетворень:

• матриця повороту (rotation) точки відносно початку координат у додатному напрямку:

• матриця розтягу (стиску) (dilation) відносно початку координат:

• матриця перенесення (translation) точки на вектор (m, n):

• матриця дзеркального відображення (reflection) відносно осі x:

Перетворення системи координат задається матрицями:

•R(–ϕ) – поворот системи координат на кут ϕ у додатному напрямі;

•T(–m, –n) – зсув системи координат на вектор (m, n).

Зауважимо, що для простоти запису аргументи наведених матриць іноді опускаються.

Елементи довільної матриці афінного перетворення (11.7) не несуть в собі явно вираженого геометричного змісту. Для того, щоб реалізувати відображення (11.7), потрібно знайти елементи матриці, виходячи з геометричного опису перетворення. Як правило, побудову такої матриці в залежності від складності задачі розбивають на кілька етапів, що

y M′(x′, y′)

ϕ M(x, y)

O

Рис. 11.5. Поворот точки M у додатному напрямку відносно точки N

209

відповідають основним елементарним перетворенням, які володіють повністю визначеними геометричними властивостями.

Розглянемо приклади складніших афінних перетворень на площині.

11.2. Приклади афінних перетворень на площині

Приклад 1. Побудувати матрицю повороту точки M(x, y) відносно довільної точки N(m, n) на кут ϕ у додатному напрямку (рис. 11.5).

Матриця R задає поворот точки відносно початку координат. Однорідні координати дають можливість знайти матрицю повороту відносно довільної точки. У загальному випадку поворот відносно довільної точки може бути реалізований шляхом таких перетворень:

1)переміщення точки N(m, n) на вектор (–m, –n) так, щоб центр повороту сумістився зпочатком координат. Матриця цього перетворення

2)повороту точки на кут ϕ у додатному напрямку відносно початку координат. Матриця цього перетворення R визначається форму-

лою (11.8);

3)переміщення одержаного результату назад так, щоб центр повороту сумістився з точкою N. Матриця цього перетворення T випи-

сана в (11.10).

Отже, для знаходження результуючого повороту точки M(x, y) відносно точки N(m, n) потрібно перемножити матриці T–, R, T за вказаним порядком.

У результаті одержимо шукане перетворення у вигляді

Зокрема, поворот точки на 900 у додатному напрямку відносно точки N(m, n) виконується перетворенням

210