kniga

Приклад 2. Побудувати матрицю неоднорідного масштабування з коефіцієнтом a вздовж осі x та коефіцієнтом b уздовж осі y з центром у точці N(m, n).

Це перетворення реалізуємо за допомогою трьох перетворень:

1)переміщення точки на вектор N(–m, –n). Матрицею цього перетворення є матриця T– ;

2)розтягу вздовж координатних осей із коефіцієнтами a та b відповідно. Матриця D цього перетворення визначається формулою

(11.9);

3)перенесення одержаного результату на вектор N(m, n). Матриця T

цього перетворення має вигляд (11.10).

Перемножуючи ці матриці, одержуємо шукане перетворення

Аналогічно, виділяючи послідовність операцій перенесення, повороту та масштабування (ці перетворення описуються матрицями T, R, D), можна побудувати матрицю для будь-якого складного афінного перетворення. Тоді афінне перетворення об’єктів на площині можна здійснити так: якщо об’єкт задається сукупністю точок, то складаємо матрицю X однорідних координат точок цього об’єкта і цю матрицю множимо на матрицю складного афінного перетворення.

Розглянемо приклад симетричного відображення трикутника відносно прямої L.

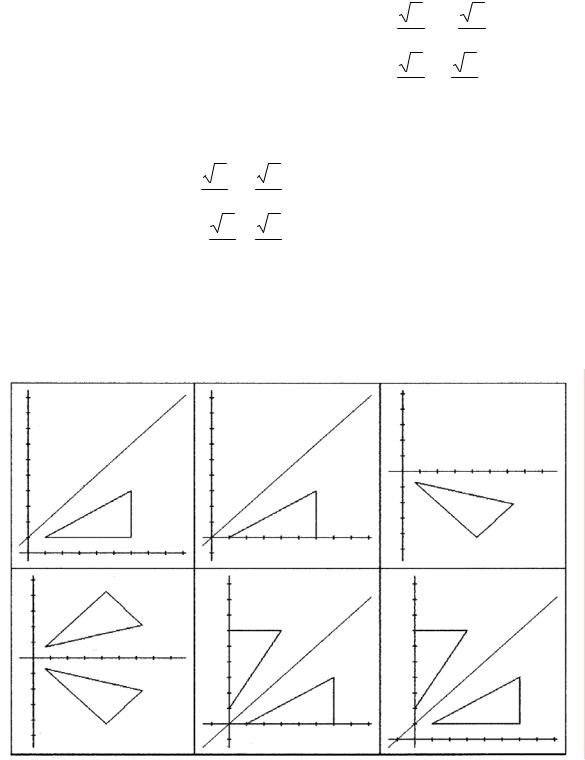
Приклад 3. Нехай пряма L задається рівнянням y = x + 1, а однорідні координати A(1; 1; 1), B(6; 1; 1), C(6; 4; 1) задають координати вершин трикутника ABC. Побудувати трикутник, симетричний даному відносно прямої L.

Представимо перетворення симетрії точки відносно прямої у вигляді послідовності простіших афінних перетворень (рис. 11.6):

•переміщення лінії та трикутника так, щоб лінія L пройшла через початок координат. Це перетворення задає матриця T із парамет-

рами (0, –1);

•поворот лінії та об’єкта відносно початку координат до збігу лінії L

звіссю x. Це перетворення задає матриця R із кутом ϕ = − π4 (у

від’ємному напрямку);

•відображення відносно координатної осі x;

•обернений поворот відносно початку координат;

211

• паралельне перенесення у вихідне положення.

Останні три перетворення задаються матрицями Ref, R(–ϕ) та T(0, 1), відповідно. У матричному вигляді перетворення симетрії має вигляд

(x′ y′ 1) = (x y 1) T(0, –1) R( − π4 ) Ref R( π4 ) T(0, 1).

Для симетрії трикутника ABC відносно прямої L маємо

Отже, декартові координати вершин симетричного трикутника

A′B′C′ мають значення A′(0; 2), B′(0; 7), C′(3; 7).

Рис. 11.6. Побудова симетричного трикутника

212

11.3. Афінні перетворення в просторі

Розглянемо тепер тривимірний випадок – 3D-перетворення простору. Всі перетворення будемо здійснювати в правосторонній системі координат Оxyz, тобто в системі координат, в якій із кінця осі z поворот від осі x до осі y бачимо проти годинникової стрілки. Якщо з вершини z поворот від x до y видно за годинниковою стрілкою, то така система координат називається лівосторонньою. У тривимірному випадку можна ввести однорідні координати так, що декартовим координатам (x, y, z) відповідатиме вектор (hx, hy, hz, h), h ≠ 0, координати якого визначаються однозначно з точністю до множника h. Запропонований підхід (введення однорідних координат) дає можливість використовувати

матричний запис всіх афінних перетворень у просторі, тобто у вигляді

(x′ y′ z′ 1) = (x y z 1) А,

де А – матриця афінного перетворення, для якої detА ≠ 0.

Зауважимо, що у випадку detА = 0 перетворення А називається про-

ективним.

Розглянемо елементарні перетворення в тривимірному просторі і побудуємо відповідні їм матриці перетворень.

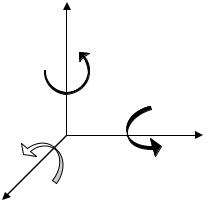
а) На відміну від 2D-випадку, в 3D-просторі визначаються три основні повороти: відносно осі x, відносно осі y, відносно осі z. При повороті точки в просторі відносно осей правосторонньої системи координат додатні напрями поворотів показані на рис. 11.7. Тобто додатними вважаються повороти від x до y , від y до z, від z до x.

y

Рис. 11.7. Додатні напрями поворотів

x

O

z

Поворот простору відносно осі z на кут χ проти годинникової стрілки відповідає додатному повороту в площині xy (якщо дивитися з кінця вектора z), z-координата залишається при цьому незмінною. Фактично поворот проходить у площинах, перпендикулярних осі z, тому матриця такого повороту одержується з матриці двовимірного повороту і має вигляд

213

Поворот проти годинникової стрілки відносно осі x на кут ϕ відповідає додатному повороту в площині yz, тобто це обертання аналогічне попередньому з точністю до перейменування осей (x → y, y → z, z → x), тому переставляючи рядки і стовпці матриці (11.12) одержуємо матрицю повороту відносно осі x

Аналогічно матриця повороту точки відносно осі y на кут ψ проти годинникової стрілки має вигляд

Для побудови матриці повороту системи координат у додатному напрямку потрібно у формулах (11.12) – (11.14) значення кутів змінити на їх протилежні значення, тобто поворот системи координат здійснюється інвертованими матрицями, а інверсія матриць повороту виконується шляхом транспонування.

Наприклад, поворот системи координат на кут χ відносно осі z у додатному напрямку задається матрицею

б) Розтяг (стиск) вздовж осей x, y, z із коефіцієнтами α, β, γ відповідно задається матрицею

214

Якщо α = β = γ = s, то маємо однорідне масштабування: при s > 1 – однорідне розтягування, при s < 1 – однорідний стиск.

в) Матриці дзеркального відображення відносно координатних площин xy, yz, zx мають вигляд

г) Перенесення (зсув) простору на вектор (l, m, n) описується матрицею

тобто однорідні координати зміщеної точки одержуються за допомогою перетворення

(x′, y′, z′, 1) = (x, y, z, 1) T.

Зауважимо, що, коли необхідно зробити кілька тривимірних поворотів, то треба мати на увазі некомутативність цих перетворень. Щоб продемонструвати цей факт, розглянемо дві послідовності поворотів на один і той же кут – спочатку відносно осі x, а потім відносно осі y і навпаки. Використовуючи матриці (11.13) та (11.14) при ψ = ϕ, одержимо

З іншого боку, поворот спочатку відносно осі y, а потім відносно осі x з кутом ψ = ϕ дає матрицю

215

Порівнюючи матриці Rxy та Ryx, бачимо, що вони різні, тобто перетворення повороту в просторі некомутативне. Комутативними є лише перетворення перенесення-перенесення і масштабування-масшта- бування.

Послідовні перетворення можуть бути об’єднані в одне перетворення, що дає той самий результат, але, оскільки множення матриць є некомутативною операцією, то важливий порядок їх виконання. Аналогічно до 2D-випадку, для 3D-простору правильною є наступна теорема.

Теорема. Довільне афінне перетворення в 3D-просторі можна подати у вигляді послідовності елементарних перетворень а) – г).

Нагадаємо, що загальна форма афінних перетворень у просторі задається системою рівнянь

x′= ax + by + ez + m, y′= cx + dy + fz + n, z′= gx+ hy + pz + l,

де (x′ , y′ , z′) – точки (вектори), що одержуються в результаті цих перетворень.

Розглянемо приклади складніших перетворень, які подамо у вигляді композиції елементарних перетворень.

11.4. Приклади складніших 3D-перетворень

Приклад 4. Побудувати матрицю повороту відносно прямої, паралельної координатній осі.

Матриці Rx, Ry, Rz описують повороти відносно координатних осей, однак часто необхідно обертати об’єкт відносно осей, що не збігаються з координатними.

Розглянемо окремий випадок повороту відносно локальної осі x′, яка паралельна до осі x. Локальна вісь x′ проходить через точку O′(0, m, n). Обертання тіла відносно локальних осей виконується за допомогою такої послідовності перетворень:

216

•зсув об’єкта так, щоб локальна вісь збігалася з координатною;

•поворот об’єкта відносно координатної осі x;

•переміщення перетвореного об’єкта у вихідне положення.

Ці перетворення можна записати у вигляді добутку матриць

X′ = X T Rx T–1,

де X′ – матриця координат перетвореного об’єкта, X – матриця координат вихідного об’єкта, T – матриця переміщення на вектор (0, –m, –n), Rx – матриця повороту відносно осі x, T– – обернена матриця до матриці переміщення.

Використовуючи формули (11.13), (11.17), одержуємо

Приклад 5. Побудувати матрицю обертання на кут θ відносно прямої L, що проходить через точку A(x0 , y0 , z0) з напрямним вектором

(a, b, с) (рис. 11.8).

(a, b, c)

z

L

A

у

O

х

Рис. 11.8. Обертання відносно довільної прямої

Нехай (a, b, c) – одиничний вектор. Узагальнений випадок обертання відносно довільної осі в просторі зустрічається часто, наприклад у робототехніці. Основна ідея розв’язування цієї задачі полягає в суміщенні прямої L з однією з координатних осей. Для цього потрібно виконати наступні кроки.

217

1)Перенесення простoру на вектор (–x0, –y0, –z0) за допомогою матриці

в результаті якого пряма L пройде через початок координат.

2)Виконання відповідних поворотів, щоб вісь обертання збіглася, наприклад, із віссю аплікат.

Узагальному випадку, щоб довільна пряма, що проходить через початок координат, збіглася з однією з координатних осей, необхідно зробити два послідовних повороти відносно двох інших координатних осей. Для суміщення довільної осі обертання з віссю z спочатку виконуємо поворот відносно осі x, а потім – відносно y.

Щоб визначати кут повороту ϕ відносно осі x, спершу спроектуємо на площину Оyz напрямний вектор (a, b, c) (рис. 11.9, а). Спроектований

вектор має координати (0, b, c). Довжина його проекції d = b2 + c2 .

Рис. 11.9. Суміщення вектора ОР з віссю z

Якщо здійснити такий поворот відносно осі x на кут ϕ, то пряма L суміститься з площиною Оxz і займе положення ОР′′(рис. 11.9, б). Під

218

дією цього перетворення координати вектора (a, b, c, 1) зміняться на

(a′, b′, c′, 1), де

(a′ b′ c′ 1) = (a b c 1) Rx = (a 0 d 1).

Далі, щоб сумістити напрям OP″ із віссю z, необхідно виконати поворот відносно осі y в напрямку від x до z, тобто за годинниковою стрілкою (у від’ємному напрямку) на кут ψ. З рис. 11.9, б маємо

sinψ = a, cosψ = d.

Відповідно матриця такого повороту має вигляд

3)Виконання повороту відносно прямої L на кут θ. Оскільки пряма L лежить на осі z, то відповідна матриця повороту в додатному напрямку має вигляд

4) Виконання перетворення, оберненого до повороту відносно осі y на кут ψ. Це перетворення описується матрицею

5)Виконання перетворення, оберненого до обертання відносно осі x на кут ϕ. Це перетворення задається матрицею

(x0, y0, z0). Це перетворення задає матриця

219

Перемноживши знайдені матриці в порядку їх побудови, одержимо матрицю повороту відносно довільної прямої L у вигляді

M = T– Rx Ry− Rz Ry Rx− T.

Загальний вигляд матриці M не виписуємо через її громіздкий запис. На практиці при написанні програм для знаходження матриці M користуються саме останньою формулою.

Розглядаючи довільні перетворення в просторі, в результаті їх ком-

Матрицю A розміром 4 × 4 можна розбити на 4 окремих частини (блоки). Верхній лівий блок розміром 3 × 3 задає сумарні лінійні перетворення: масштабування, поворот, відображення. Лівий нижній задає переміщення, правий верхній – перспективні перетворення (див. п. 12.5). Елемент a44 = 1 – загальний коефіцієнт масштабування.

За допомогою матриці A можна перетворювати довільні просторові фігури, наприклад здійснювати перетворення опуклого многогранника. Опуклий многогранник однозначно визначається набором своїх вершин Xi(xi, yi, zi), що утворюють матрицю X. Далі на матрицю X діємо невиродженою матрицею A і одержуємо набір вершин X′ = X A нового многогранника, який є образом вихідного многогранника.

11.5. Методи задання складних афінних перетворень

Складним (комбінованим) називається перетворення, яке містить ланцюжок базових перетворень (не менше двох). Зауважимо, що майже

220