kniga

знаходимо

Якщо |M| = 0, то відрізки паралельні. У випадку непаралельності відрізків умови 0 ≤ t ≤ 1, 0 ≤ τ ≤ 1 визначають існування точки перетину двох відрізків.

Алгоритм розрахунку точки перетину відрізків ab та cd, повертає ознаку перетину:

•–1, якщо прямі відрізків паралельні;

•0, якщо непаралельні відрізки не перетинаються;

•1, якщо відрізки перетинаються

імає такий вигляд [21]:

cross_segm(ab, cd, t, τ, q)

повертаємо (0 ≤ t ≤ 1) I (0 ≤ τ ≤ 1) // ознака перетину відрізків Цей алгоритм вимагає максимально 11 операцій додавання і 10

операцій множення/ділення.

9.5. Алгоритми відсікання

Процес виділення тієї частини геометричного об’єкта, яка лежить поза видимою областю (вікном), називається відсіканням (clipping).

Задачі відсікання видимого зображення по границях деякої області в комп’ютерній графіці зустрічаються досить часто. Вони є головними геометричними задачами при візуалізації геометричних об’єктів. У простіших випадках областю відсікання виступає прямокутник (рис. 9.7).

161

Часто графічні зображення складаються із сукупності відрізків. Для задачі відсікання за допомогою алгоритму cross_segm можна було б розрахувати ті частини відрізків, які знаходяться зовні вікна. Однак це потребує виконання великої кількості відповідних обчислень. Графічні об’єкти складаються з відрізків трьох типів: цілком видимі, цілком невидимі і частково видимі (рис. 9.7).

a

Рис. 9.7. Двовимірне відсікання прямокутним вікном

9.5.1. Двовимірний алгоритм Сазерленда-Коена

Алгоритм Сазерленда-Коена достатньо просто й ефективно дозволяє прийняти або відсікти відрізки цілком відносно довільного прямокутника. У цьому алгоритмі для двох кінців відрізка будуються 4-бітні коди (зліва направо):

біт 0 визначає чи точка лежить лівіше вікна; біт 1 визначає чи точка лежить вище вікна; біт 2 визначає чи точка лежить правіше вікна; біт 3 визначає чи точка лежить нижче вікна.

Біт набуває одиничного значення, якщо умова істинна, і нуль, якщо умова хибна. Тобто площина з вікном чотирма прямими розбивається на 9 областей, у кожній з яких є свій код (рис. 9.8). Ці коди використовуються для визначення чи знаходиться відрізок повністю у вікні чи зовні вікна.

Отже, маємо такий алгоритм відсікання відрізків.

•Формуємо коди (код1 та код2) для кінців відрізка.

•Якщо два коди для кінців відрізка дорівнюють 0000, то відрізок повністю знаходиться у вікні.

•Відрізок цілком відсікається, якщо код1 and код2 ≠ 0000.

162

ребрами вікна, причому оскільки відомо, в які області попадають кінці відрізка, то, аналізуючи коди кінців відрізка, легко зрозуміти,

зякими саме ребрами вікна може перетинатися відрізок.

9.5.2.Відсікання відрізка опуклим полігоном

Алгоритм повертає через аргумент ab фрагмент відрізка, що потрапляє всередину полігона й ознаку видимості відрізка ab у вікні полігона P, що приймає значення

•0, якщо відрізок повністю знаходиться зовні полігона і відсікається цим полігоном;

•1, якщо відрізок повністю або частково розміщений усередині

полігона.

Робота алгоритму починається з ініціалізації лічильника перетинів k = 0. Далі виконується обхід ребер полігона Pi Pi + 1 для i = 1, 2,…, n (Pn+1=P1) і розрахунок перетину з ними не самого відрізка ab, а прямої, що містить цей відрізок (це можна зробити за допомогою функції cross_segm).

Якщо пряма перетинає ребро (це розпізнається за умовою 0 ≤ τ ≤ 1), то лічильник перетинів k інкрементується, а параметр t зберігається у змінній σk, k = 1, 2. Якщо знайдено два перетини (k = 2), то подальший обхід полігона припиняється (саме тому розраховується перетин ребер полігона з прямою, що містить відрізок ab, а не з самим відрізком).

Кінцеві точки видимої частини відрізка [a, b] визначаються за допомогою значень σ1 = ti, σ2 = tj параметра t, при яких пряма перетнула ребра Рi Рi + 1 та Рj pj + 1:

•значення {σ1 < 0, σ2 > 1} і {σ1 > 1, σ2 < 0} відповідають розміщенню всього відрізка [a, b] у вікні полігона і відсікання не виконується;

•значення {σ1 < 0, σ2 < 0} або {σ1 > 1, σ2 > 1} повністю відсікають відрізок;

163

•значення {0 ≤ σ1 ≤ 1, σ2 < 0} повертають відрізок [a, a + Vσ1];

•значення {0 ≤ σ1 ≤ 1, σ2 > 1} повертають відрізок [a + Vσ1, b];

•значення {σ1 < 0, 0 ≤ σ2 ≤ 1} повертають відрізок [a, a + Vσ2];

•значення {σ1 > 1, 0 ≤ σ2 ≤ 1} повертають відрізок [a + Vσ2, b];

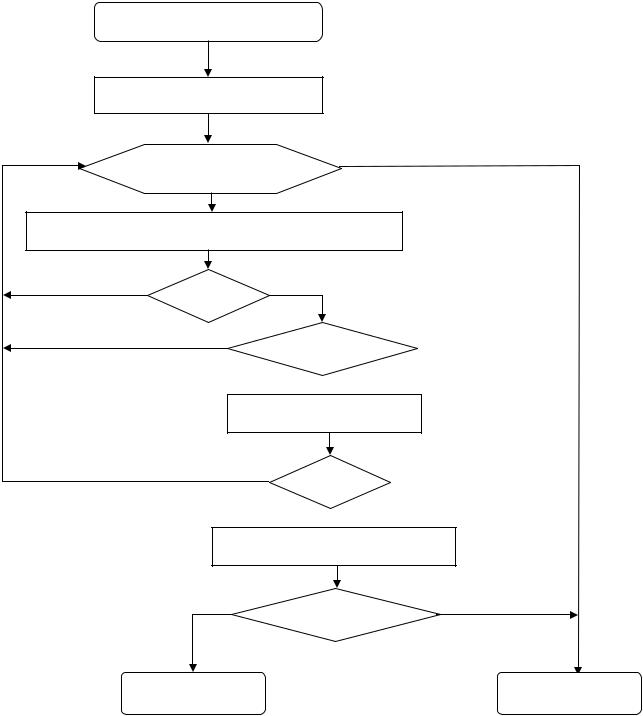
•значення {0 ≤ σ1 ≤ 1, 0 ≤ σ2 ≤ 1} стягують кінцеві точки відрізка [a, b] на границю полігона – в точки a + Vσ1 і a + Vσ2, V=b – a. Блок-схему цього алгоритму подано на рис. 9.10 [21].

clip2_cross(ab, P)

k = 0, V = b – a

c = cross_segm(ab, pipi + 1, t, τ, q)

так

k = k + 1, σk = t

так

k < 2

ні

Розрахунок ab за σ1, σ2

повертаємо 1 повертаємо 0

Рис. 9.10. Блок-схема алгоритму відсікання

164

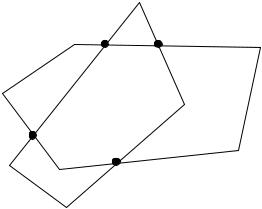
9.5.3. Перетин та об’єднання опуклих полігонів

•Спочатку функцією clip2_cross(AiAi+1, B), i = 1, 2, …, n виконуємо зовнішнє відсікання ребер полігона A полігоном B. У результаті одержуємо список відрізків Ls = {Q1A2, A2Q2, Q3Q4}.

•Далі функцією clip2_cross(BjBj + 1, A), j = 1, 2, …, m виконуємо зовнішнє відсікання ребер полігона B полігоном A і додаємо в список Ls нові відрізки B1Q2, Q1Q4, Q3B1.

•З елементів одержаного списку

Ls = {Q1A2, A2Q2, Q3Q4, B1Q2, Q1Q4, Q3B1}

збираємо замкнутий контур шляхом з’єднання відрізків збіжними кінцями. Для цього беремо перший відрізок Q1A2 і серед інших елементів списку Ls шукаємо відрізок, кінець якого збігається з A2. Це відрізок Q2A2, який разом із відрізком Q1A2 утворює ламану C = {Q1A2Q2}. Далі знаходимо продовження ламаної B1Q2 і одержуємо ламану C = {Q1A2Q2B1} і т.д., поки не одержимо замкнений контур C = {Q1A2Q2B1Q3Q4Q1}. Якщо полігони не перетинаються, то після виконання зовнішнього відсікання список Ls буде порожнім.

9.6.Інші алгоритми відсікання відрізків

Вбагатьох випадках більшість відрізків лежить цілком всередині або зовні відсікаючого вікна, тому необхідно мати можливість якомога раніше без складних обчислень визначити, які з відрізків цілком видимі,

аякі цілком невидимі і їх можна зразу відкинути. Задачу відсікання можна розв’язувати різними методами.

За способом розв’язування цієї задачі всі алгоритми відсікання поділяються на 2 класи [7]:

165

–алгоритми, що використовують коди кінців відрізка або самого відрізка;

–алгоритми, що використовують параметричне задання самих відрізків і сторін вікна.

До першого класу алгоритмів належить алгоритми СазерлендаКоена, FC-алгоритм, до другого класу – алгоритм Кіруса-Бека, ЕйлераАзертона і більш пізній алгоритм Ліанга-Барскі та ін.

Алгоритми з кодуванням застосовуються до прямокутних вікон, сторони яких паралельні осям координат, а алгоритми з параметричним заданням – до будь-яких вікон.

Вище ми вже розглянули алгоритм Сазерленда-Коена, який є стандартом для алгоритмів відсікання. Розглянемо тепер FC-алгоритм.

9.6.1.Двовимірний FC-алгоритм

Вцьому алгоритмі кодуються не кінці відрізка, а весь відрізок цілком. Схема кодування близька до тієї, що використовується в алгоритмі Сазерленда-Коена.

Площина з вікном розбивається на 9 областей і вони кодуються цифрами від 1 до 9 (рис. 9.12). Область з вікном має код 5.

Рис. 9.12. Коди областей для FC-алгоритму

Відрізок кодується наступним чином:

LineCode(ab) = Code(a)* 10 + Code(b),

Code(a) – код області з початковою точкою відрізка, Code(b) – код області з кінцевою точкою відрізка, LineCode(ab) – код відрізка.

Оскільки кожний код може набувати дев’ять значень, то існує 81 можливий варіант розміщення відрізка і для кожного варіанту, тобто для кожного коду відрізка необхідно мати свій набір обчислень для відсікання відрізка.

Якщо Code(a) = Code(b), то LineCode(ab) = LineCode(ba). Існує 9

таких випадків: (1 – 1), (2 – 2), …, (9 – 9).

У випадку (5 – 5) (код відрізка 55) відрізок повністю видимий, у решті випадків – частково або повністю невидимий.

166

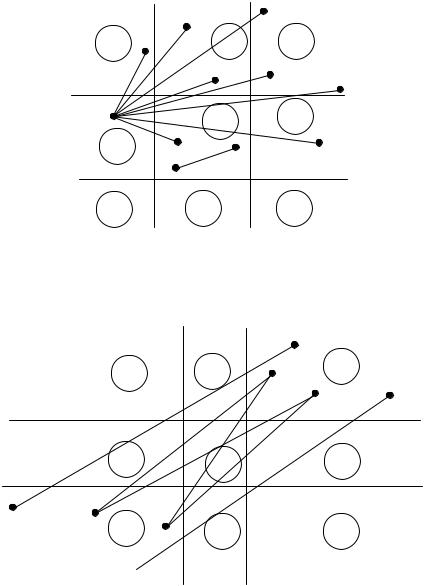
Отже, кількість різних варіантів тепер зменшується до 72, але і серед них існує всього 6 основних випадків відсікання, решта – симетричні їм. Для того, щоб виділити ці 6 випадків, потрібно розглянути різні варіанти розміщення відрізка для некутових та кутових областей. Ілюстрації можливих варіантів розміщення відрізка для перших п’яти випадків наведені на рис. 9.13, для шостого випадку – на рис. 9.14.

Рис. 9.13. Варіанти розміщення відрізка для некутових областей

U

Рис. 9.14. Варіанти розміщення відрізка для кутових областей

Випадок 1 – початкова точка відрізка знаходиться в області 4, а кінцева – в області 1 (відрізок AB, LineCode = 41). Відрізок не перетинає видиму область і відкидається.

Випадок 2 – початкова точка відрізка знаходиться в області 4, кінцева – в області 2. Це відрізки AC і AD, LineCode = 42. Вони перетинають ліву межу вікна. Знайдемо точки перетину відрізків AC і

167

AD з лівою межею вікна – (xлів, yn). Якщо yn > yверхн, то це відрізок AC, він не перетинає відрізка з лівим ребром видимої області й відкидається.

Якщо yn < yверхн, то це відрізок AD, що перетинається також з верхньою межею вікна. Тому необхідно обчислити точку перетину відрізка AD з

верхньою межею вікна й зобразити видиму частину відрізка.

Випадок 3 – початкова точка відрізка знаходиться в області 4, кінцева – в області 3 (відрізки AE, AF і AG, LineCode = 43). Обчислюємо

точки перетину відрізків з лівим ребром вікна (xлів, yn). Якщо yn > yверхн, то це відрізок AE. Він не перетинає видиму область і відкидається, інакше

це відрізки AF і AG. Для них обчислюємо точку перетину з правим

ребром (xпр, yn). Якщо yn > yверхн, то це відрізок AF, тому необхідно обчислити точку перетину з верхнім ребром вікна і зобразити видиму

частину відрізка. Інакше це відрізок AG, для нього вже точки перетину з ребрами вікна знайдені, залишається зобразити лише видиму частину відрізка.

Випадок 4 – початкова точка відрізка знаходиться в області 4, кінцева – в області 6 (відрізок AH, LineCode = 46). Обчислюємо точки перетину відрізка з лівим і правим ребрами вікна і зображаємо видиму частину відрізка.

Випадок 5 – початкова точка – в області 4, кінцева – в області 5 (відрізок AL, LineCode = 45). Обчислюємо точку перетину відрізка з лівим ребром і зображаємо видиму частину відрізка.

Випадок 6 – початкова точка знаходиться в області 7, кінцева – в області 3 (відрізки RW, SX, SY, TX, TY, UV, LineCode = 73). Обчислюємо

точку перетину відрізка з лівим ребром (xлів, yn1). Якщо yn1 > yверхн, то це відрізок RW і він відкидається. Обчисляємо точку перетину з правим

ребром (xпр, yn2). Якщо yn2 < yнижн, то це відрізок UV, він теж відкидається. При yn1 > yнижн це або відрізок SX, або SY. Далі, якщо yn2 < yверхн, то це відрізок SY і можемо зобразити його видиму частину. Інакше

це відрізок SX, тому необхідно обчислити точку перетину з верхнім ребром вікна і зобразити його видиму частину. Залишилося розглянути

відрізки TX, TY. Якщо yn2 < yверхн, то це відрізок TY і ми можемо зобразити його видиму частину. Інакше це відрізок TX, тому обчисляємо

для нього точку перетину з верхньою стороною вікна і теж відображаємо його видиму частину.

Зауваження. Для більш швидкої роботи алгоритму можна використовувати коди в шістнадцятковій системі числення, що визначаються зі співвідношення

LineCode(ab) = Code(а) shl 4 + Code(b).

168

Вказівка. Для побудови програми можна скористатися оператором switch і задати дії для кожного з 81 випадків.

9.6.2. Алгоритм Кіруса-Бека

Попередні алгоритми виконували відсікання прямокутним вікном, сторони якого паралельні осям координат. Однак в багатьох випадках потрібне відсікання довільним многокутником, наприклад в алгоритмах усунення невидимих частин сцени.

Алгоритм Кіруса-Бека реалізує відсікання довільним опуклим вікном і базується на методі визначення орієнтації лінії, яка містить відрізок, що відсікається, по відношенню до сторони многокутника, а також на методі визначення місцезнаходження точки відрізка відносно вікна – всередині, на границі або зовні вікна. Для цього в алгоритмі Кіруса-Бека використовується вектор внутрішньої нормалі до ребра вікна.

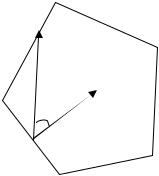
Розглянемо опуклу двовимірну область P, тобто опуклий многокутник. Внутрішньою нормаллю n до сторони вікна називається нормаль, яка направлена в бік області, що складає вікно відсікання. Як видно з рис. 9.15, внутрішня нормаль n у точці a, що лежить на границі, задовольняє умову

де b – будь-яка інша точка границі опуклої області P. b

nРис. 9.15. Визначення місцезнаходження точки

θвідносно вікна відсікання в алгоритмі Кіруса-Бека

a

Скалярний добуток в (9.4) для внутрішньої нормалі n невід’ємний тому, що θ [0, π2 ], тобто cosθ ≥ 0.

Зазначимо, що внутрішні нормалі можна обчисляти й іншим способом. Для цього необхідно полігон обходити за годинниковою стрілкою і вибирати нормалі, які направлені вправо від кожного ребра (див. п.9.1.1).

Нехай ni – внутрішня нормаль до i-ї граничної лінії многокутного вікна, а V = b – a – вектор, що визначає орієнтацію відрізка ab, який відсікається вікном P. Тоді орієнтація відрізка ab відносно i-ї сторони вікна визначається знаком скалярного добутку ri = (ni V):

169

−при ri < 0 відрізок ab направлений з внутрішньої сторони на зовнішню сторону i-ї граничної лінії вікна (рис. 9.16, а).

−при ri = 0 точки a, b або збігаються (відрізок вироджується в точку) або відрізок ab паралельний i-й стороні вікна (рис. 9.16, б).

−при ri > 0 відрізок ab направлений із зовнішньої сторони на внутрішню сторону i-ї граничної лінії вікна (рис. 9.16, в).

Рис. 9.16. Орієнтація відрізка ab відносно сторони вікна: а -- зсередини назовні; б – паралельно границі; в – ззовні всередину

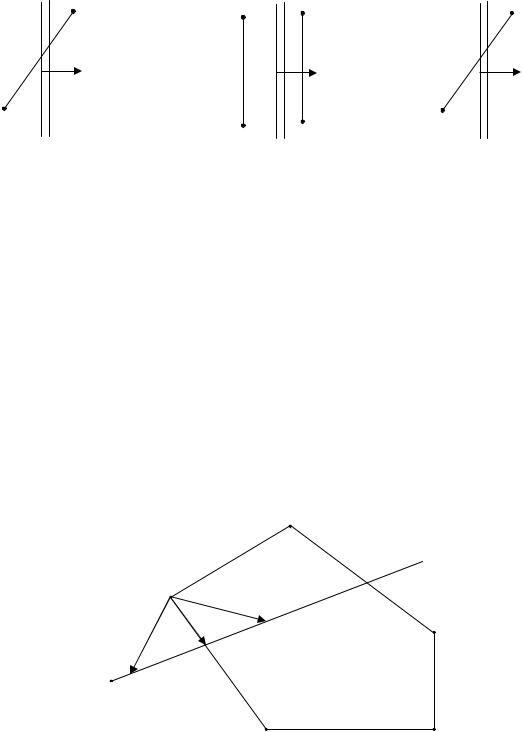
Для визначення розміщення точки V(t) відрізка ab відносно i-ї сторони вікна розглянемо скалярний добуток внутрішньої нормалі ni на вектор Qi = V (t) – Pi, що починається в початковій точці Pi ребра вікна і закінчується в деякій точці V(t) відрізка ab, а саме

qi = (ni Qi ), i =1, 2, … (9.5)

Аналогічно попередньому маємо (рис. 9.17):

−якщо qi < 0, то точка V(t) лежить із зовнішньої сторони границі;

−якщо qi = 0, то точка V(t) лежить на лінії границі вікна;

−якщо qi > 0, то точка V(t) лежить із внутрішньої сторони i-ї границі вікна.

b

a V(t) V(t)

Рис. 9.17. Розміщення точки відносно границі вікна

170