
kniga
.pdf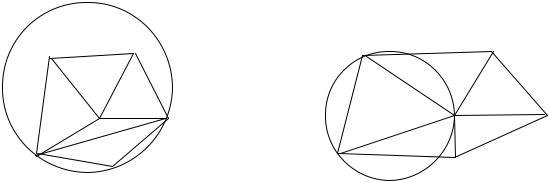
P1 P2 P3 P5 P6 P7 P8 P1 , до якого необхідно застосувати ті ж самі операції, що і для вихідного полігона і т.д., поки полігон, який залишається, не стане трикутником.
Зауваження 6. Задачу тріангуляції можна розв’язувати й іншим способом, наприклад, методом розрізування полігона хордами – продовженнями його ребер, що складають неопуклу вершину, на кілька опуклих підполігонів. Далі опуклі підполігони розрізуємо діагоналями на трикутники.
9.8.3. Тріангуляція Делоне
Розглянемо задачу тріангуляції набору точок S на площині. Усі точки набору S повинні лежати у вершинах трикутників. Ребра трикутників не повинні перетинатися. Усі точки набору S можна розбити на граничні точки, тобто на такі, які лежать на границі опуклої оболонки, і внутрішні, що лежать усередині опуклої оболонки. Так само можна класифікувати й ребра, що одержуються в результаті тріангуляції, – ребра оболонки і внутрішні ребра.
Будь-який набір точок S, за винятком деяких тривіальних випадків, допускає більше одного способу тріангуляції і при цьому одержується одна і та ж сама кількість трикутників (рис. 9.28 ). За теоремою Ейлера кількість трикутників не перевищує 2n, де n – кількість точок масиву S.
Серед усіх можливих тріангуляцій виділяється спеціальний вид – тріангуляція Делоне [26]. Ця тріангуляція характеризується тим, що утворені трикутники наближаються до максимально правильних.
Означення. Тріангуляція набору точок S називається тріангуляцією Делоне, якщо всередині кола, описаного навколо кожного трикутника, немає точок набору S, окрім їх вершин.
p2 |
p3 |
|
p2 |
p3 |
|
|
|
|
|
p6 |
p4 |
|
p6 |
p4 |
p1 |
p5 |
p1 |
p5 |
|
а |
|
|
||
|
|
б |
|
Рис. 9.28. Тріангуляція набору точок
Тріангуляцію, що зображена на рис. 9.28, а, не можна віднести до тріангуляції Делоне, а тріангуляція на рис. 9.28, б є тріангуляцією Делоне.
181
Використовуючи означення тріангуляції Делоне, можна розробити алгоритм її побудови, час роботи якого прямо пропорційний кількості точок масиву S, і виконана побудова є однозначною [38].
Задачі тріангуляції виникають, наприклад, при побудові ізоліній функцій двох змінних, які задані множиною дискретних значень на нерегулярній сітці. Зокрема, це задачі створення топографічних карт, які є картами ізоліній функції висоти рельєфу місцевості: на практиці значення цих функцій найчастіше доступні лише в точках скінченної нерегулярної множини.
Контрольні питання та завдання
1.Як перевірити напрям обходу трьох точок?
2.Як визначити чи опуклий полігон?
3.Як визначити чи пряма лінія перетинається з полігоном?
4.В чому суть габаритного тесту?
5.Сформулюйте основну ідею променевого тесту.
6.На яких ідеях ґрунтується кутовий тест?
7.Як визначити перетин двох відрізків?
8.На площині задано два трикутники. Як визначити чи трикутники перетинаються, чи один трикутник лежить всередині іншого?
9.В чому полягає суть задачі відсікання?
10.Яка основна ідея алгоритму Сазерленда-Коена?
11.Як будуються двійкові коди в алгоритмі Сазерленда-Коена?
12.Як знаходяться кінцеві точки видимої частини відрізка при відсіканні його опуклим полігоном?
13.Як визначити внутрішню/зовнішню нормаль ребра опуклого многокутника?
14.Як знайти перетин опуклих полігонів?
15.Як класифікуються алгоритми відсікання?
16.Як утворюється коди відрізків в FC-алгоритмі?
17.Як здійснюється відсікання відрізків, якщо їх код дорівнює 73?
18.Яка основна ідея алгоритму Кіруса-Бека?
19.Як визначається орієнтація відрізка відносно сторони вікна в алгоритмі Кіруса-Бека?
20.Опишіть основні кроки алгоритму Кіруса-Бека.
21.Які можливості має алгоритм Вейлера-Азертона?
22.Наведіть загальну схему алгоритму Вейлера-Азертона.
23.Як визначаються вершини опуклої оболонки в методі загортання подарунка?
24.Опишіть роботу алгоритма Грехема на конкретному прикладі.
25.Що таке тріангуляція полігонів?
182
26.Як виконується тріангуляція неопуклих полігонів?
27.Розкрийте поняття тріангуляції Делоне.
Вправи і задачі для самостійного виконання
1.Розробити алгоритм непараметричного пошуку перетину відрізка зі сторонами вікна шляхом поділу відрізка його навпіл.
2.Розробити алгоритм відсікання відрізків кількома вікнами, якщо вікна мають пріоритет.
3.Написати процедуру для розпізнавання опуклих многокутників шляхом обчислення векторних добутків векторів сторін.
4.Для одержання сферичного трикутника на сфері беруть три точки і з’єднують дугами. Обчислити точку перетину променя зі сферичним трикутником.
5.Розробити алгоритм визначення перетину променя з многокутником в тривимірному просторі.
6.Розробити алгоритм визначення належності точки многограннику.
7.Розробити тест опуклості просторового многокутника.
8.Розробити алгоритм аналізу двійкового коду в алгоритмі Сазерле- нда-Коена для знаходження ребра, що перетинається з відрізком.
9.Узагальнити алгоритм Сазерленда-Коена для 3D-простору.
10.Узагальнити алгоритм Кіруса-Бека для тривимірного випадку.
11.Розробити алгоритм генерування довільного полігона.
12.Узагальнити променевий тест визначення приналежності точки полігону на випадок променя з довільним напрямом V.
13.Модифікувати УХ-алгоритм для перевірки належності точки полігону.
14.Розробити тест перетину двох плоских многокутників.
15.Розробити алгоритм об’єднання опуклих полігонів.
16.Розробити алгоритм відсікання опуклого/неопуклого полігона півплощиною (рис. 9.5, а).
17.Навести приклад відсікання неопуклого многокутника з отворами іншим неопуклим многокутником з отвором. На цьому прикладі проілюструвати роботу алгоритма Вейлера-Азертона.
18.Розробити алгоритм розрізання неопуклого многокутника на опуклі многокутники, використовуючи операції повороту.
19.Розробити алгоритм відсікання многокутної зафарбованої області.
20.Розробити програму для виконання різноманітних бінарних операцій над многокутниками, що задаються в інтерактивному режимі.
183
Тема 10. Фрактали в комп’ютерній графіці
10.1. Поняття фрактала
Поняття фрактала, фрактальної геометрії з’явилося в кінці 70-х років минулого століття і стало широко застосовуватися математиками і ком- п’ютерними художниками. Фрактали знайшли широке застосування в комп’ютерній графіці завдяки компактності математичного апарату, необхідного для їх відтворення на екрані комп’ютера.
За останній час з’явилося багато праць (особливо на Заході), присвячених фракталам (наприклад, [18, 20]). В цих працях вивчаються математичні основи фракталів, а також наводяться оригінальні графічні зображення фракталів, одержаних за допомогою комп’ютерів.
Слово фрактал походить від латинського fractus і в перекладі означає “cкладений із фрагментів’’. Цей термін запропонований математиком Б. Мандельбротом у 1975 р. для позначення самоподібних структур. Поняття фрактала як математичного об’єкта досі залишається невизначеним – зроблено лише окремі спроби визначити фрактал. Перша спроба базується на топологічній розмірності множин (точка має розмірність 0, лінія – 1, плоска фігура – розмірність 2). Фігури з дробовою розмірністю описують властивості фракталів. Але це визначення не точне, оскільки трапляються фрактали з розмірністю 2. У комп’ютерній графіці використовують таке означення фрактала.
Фракталом, за Мандельбротом, називається геометрична фігура, яка складається з частин, які в певному розумінні подібні за формою на всю фігуру, тобто це геометрична фігура, в якій один і той самий фрагмент повторюється при кожному зменшенні масштабу (частина об’єкта схожа на сам об’єкт).
Характерною рисою фрактала є інваріантність (самоподібність) відносно масштабу, наприклад, гірський камінь має такі ж обриси, як і гірський хребет.
Існують конструктивні (геометричні) та динамічні (алгебраїчні)
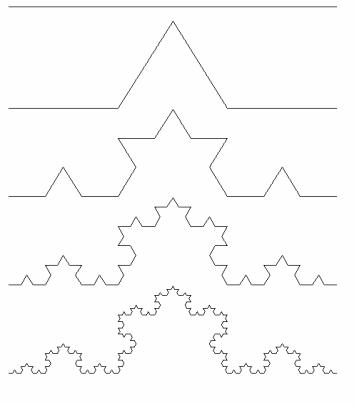
фрактали. Найбільш наочними є геометричні фрактали, оскільки їхня форма може бути описана як послідовність простих геометричних операцій. На площині їх отримують за допомогою деякої ламаної, яка називається генератором. За один крок алгоритму кожен із відрізків ламаної замінюється на ламану-генератор у відповідному масштабі. У результаті нескінченного повторення кроків цього алгоритму одержуємо геометричний фрактал. Тому алгоритми побудови фракталів в більшості випадків носять рекурсивний характер. Рекурсивність обумовлює властивість самоподібності фрактала. Прикладом геометричного фрактала є крива Коха. Послідовні наближення до фрактала Коха зображено на рис. 10.1.
184
n = 0
n = 1
n = 2
n = 3
n = 4
Рис. 10.1. Фрактал Коха
Прикладом конструктивного фрактала може бути дерево, стовбур якого розділений на менші гілки. У свою чергу кожна з цих гілок ділиться на дві менші і т.д. Практично ми зупинимося на певному кроці (уявно цей процес можна продовжити до нескінченності). Фігура, що з’явиться в результаті цих операцій і є фракталом, в якому кожна його частина у свою чергу подібна на весь фрактал (рис. 10.2).
Поряд із конструктивними фракталами були відкриті множини, схожі на фрактали (вони можуть володіти масштабною інваріантністю лише наближено). Такі множини називаються динамічними (алгебраїчними) фракталами. Як правило, вони виникають у нелінійних дискретних динамічних системах.
Якщо нелінійна система досить складна, то вона у своєму розвитку проходить етапи стійкого і хаотичного розвитку. Нелінійні системи володіють кількома стійкими станами (атракторами). Існують області початкових даних, з яких система потрапляє в область притягання атрактора. Замальовуючи області притягання різними кольорами, можна отримати кольоровий фазовий портрет цієї системи.
Динамічні фрактали одним із перших описав у 1918 р. французький математик Г. Жуліа. На той час були ще відсутні зображення фракталів. Комп’ютери зробили видимим те, чого не уявляли в часи Жуліа. Ком- п’ютерні візуальні результати перевершили всі очікування.
185
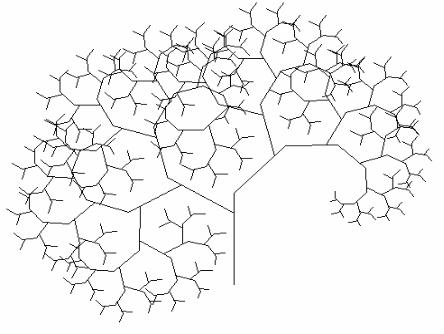
Рис. 10.2. Фрактал „дерево”
10.2. Конструктивні фрактали
Фрактали, в яких фрагменти повторюються при зменшенні масштабу, називаються конструктивними фракталами. Розглянемо математичні основи деяких конструктивних фракталів.
10.2.1.Крива Коха
У1904 р. Кох побудував криву, яка в кожній точці не має похідної, а сама крива і кожна її частина має нескінченну довжину. На рис. 10.1 зображено наближення кривої Коха. Побудову кривої Коха починаємо з відрізка-основи. Для цього усуваємо середню третю частину відрізка і замінюємо її на сторони рівностороннього трикутника. Далі чинимо аналогічно з кожним відрізком ламаної (рис. 10.1). Криву Коха можемо уявити як границю таких операцій.
Якщо основа має одиничну довжину, то ламана при n = 1 склада-
ється з 4 відрізків (кожен довжиною 1/3). При n = 2 одержуємо ламану з 16 відрізків загальною довжиною 16/9 = (4/3)2.
Якщо застосувати n = p перетворень до основи, то результатом буде ламана, що складається з 4p відрізків довжиною 1/3p. Загальна довжина цієї ламаної дорівнює (4/3)р.
Якщо p прямує до нескінченності, то довжина кожного відрізка прямує до нуля, а загальна довжина кривої Коха – до нескінченності. Крива Коха є образом одиничного відрізка [0,1], а будь-яка частина кривої Коха – мініатюрною копією всієї кривої.
Якщо за основу кривої Коха взяти сторони правильного многокутника, то можна одержати гарні зображення (варіації на тему кривої
186

Коха). Наприклад, якщо за основу взяти квадрат, а як генератор – фрагмент Коха, орієнтований назовні квадрата, то одержимо фігуру (острів Коха), що зображена на рис. 10.3 (p = 4).
Рис. 10.3. Острів Коха при p = 4
Розглянемо загальну схему побудови подібних фракталів. Припустимо, що основа складається з u відрізків, а фрагмент – із v відрізків. Вершини для основи і фрагмента повинні бути задані явно, тоді при заданому порядку апроксимації p із кожного відрізка основи одержується ламана з vp – 1 вершинами.
Розглянемо деякі випадки.
1.Основою є квадрат з одиничною довжиною. Відрізок [0, 1] замінюється фрагментом з проміжними точками (0,4; 0,2), (0,6; 0,2) (рис. 10.4, а). У результаті послідовних наближень одержимо фрактал, який називають островом Мінковського (рис. 10.4, б).
а
Рис. 10.4. Острів Мінковського (р = 6) |
б |
|
187
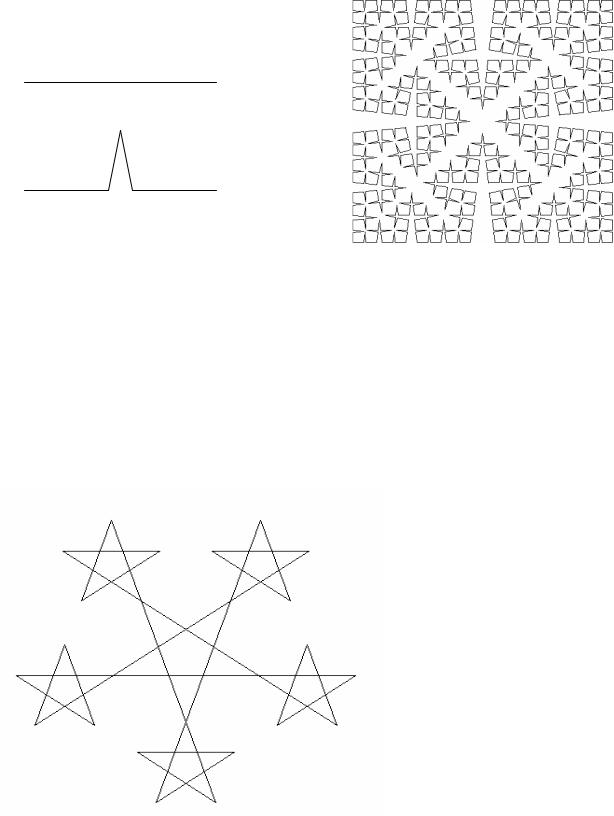
2.Основою є квадрат з одиничними сторонами, фрагментом – ламана
зпроміжними точками (0,47; 0), (0,5; 0,47), (0,53; 0) (рис. 10.5, а).
Фрактал (льодовий квадрат) зображений на рис. 10.5, б.
б
а
Рис. 10.5. Льодовий квадрат (p = 4)
10.2.2. Зіркові фрактали
Зірковий фрактал складається з п’ятикутної зірки та гірлянди з п’яти менших зірок, а кожна з п’яти зірок має чотири вільних кінці, на яких у свою чергу, знаходяться ще менші зірки. Теоретично цей процес можна продовжувати до нескінченності – в результаті одержимо зірковий фрактал. Задавши деяку кількість кроків p, одержуємо наближення зіркового фрактала. На рис. 10.6 зображено наближення зіркового фрактала при p = 2. Виконаємо нумерацію відрізків фрактала від 0 до 19 .
|
8 |
13 |
|
5 |
15 |
||
|
|||
|
6 |
16 |
|
7 |
|
|
|
|
|
14 |
|
18 |
|
3 |
|
0 |
|
1 |
|
|
|
||
17 |
|
2 |
|
19 |
10 |
4 |
|
|
11 |
||
|
|
12 9
Рис 10.6. Зірковий фрактал при р = 2
188

Зірковий фрактал можна побудувати як замкнену ламану лінію, послідовні відрізки якої завжди перетинаються під одним і тим же кутом α = π – (π/5) = 4π/5, тому що зірка є правильною і її внутрішній кут дорівнює π/5. Якщо початковий відрізок із номером n = 0 має напрям θ = 0, то відрізок із номером n має напрям θ = nα. Фрагмент фрактала зображений на рис. 10.7.
|
При побудові зіркового фрактала ми |
|
α |
повинні враховувати правило, за яким виз- |
|
n = 1 |
начається довжина n-го відрізка ламаної, |
|
n = 2 |
якщо відома довжина першого відрізка. |
|
α |
Зображений фрактал на рис. 10.6 |
|
n = 0 |
складається з відрізків двох різних дов- |
|
жин. Якщо прийняти довжину більшого |
||
|
||
|
відрізка за одиницю, то довжина меншого |
|
α |
дорівнюватиме r , де r – показник змен- |
|
|
шення (0 < r < 1). Наприклад, на рис. 10.6 |
r = 0,35. Як видно з рис. 10.6, відрізки з номерами n = 0, 4, 8, 12, 16 мають одиничну довжину, а відрізки з номерами n =
1, 2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 15, 17, 18, 19 – довжину r.
Для зіркового фрактала при p = 3 (рис. 10.8) правило довжин таке: n = 0, 16, 32,…– довжина 1;
n = 4, 8, 12, 20,…– довжина r;
n = 1, 2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 15,...– довжина r2 = rp-1.
Отже, довжина відрізка з індексом n залежить від кількості множників 4 у числі n. Загальне правило довжин відрізків ламаної для довільного числа кроків p таке:
якщо номер відрізка n не має множника 4, то його довжина rp-1 , якщо номер відрізка n має 1 множник 4, то його довжина rp-2 ,
. . . . . . . . . . . . . . . . . . . . . . . . . . .
якщо номер відрізка n має хоча би p – 1 множників 4, то довжина відрізка дорівнює 1.
У загальному випадку число відрізків зіркового фрактала обчислюється за формулою (N + 1)N p-1, де N = 4. Кількість відрізків з одиничною довжиною буде N + 1.
Наприклад, при p = 5 маємо 1280 = 5 × 44 – відрізків ламаної, з них 5 відрізків мають одиничну довжину.
Зауважимо, що значення N = 4 можна замінити на деяке інше число і тоді, визначивши відповідний кут, на який повинні повертатися відрізки ламаної, можна будувати інші зіркові фрактали.
189
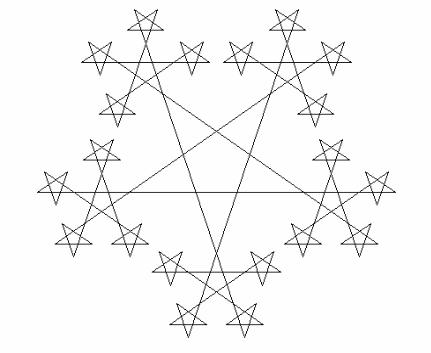
Рис. 10.8. Зірковий фрактал при р = 3
Відображення, що описує поворот точки (х2, у2) на кут α (проти годинникової стрілки) відносно довільної точки (х1, у1), має вигляд
x3 |
= (x2 |
– x1)cosα – (y2 – y1)sinα + x1, |
(10.1) |
y3 |
= (x2 – x1)sinα + ( y2 – y1)cosα + y1. |
|
|
10.3. Аналіз конструктивних фракталів
Фрактали можна визначити як множини точок інваріантних відносно перетворення поворот-стиск. У простішому випадку стиск – це масштабне зменшення з поворотом (або без нього) і задається лінійним відоб-
раженням площини (х, у) в (x´, y´), тобто |
|
x´ = ax + by, y´ = cx + dy. |
(10.2) |
Якщо det(A) = ad – cb ≠ 0, то перетворення (10.2) має єдину нерухому точку О(0,0).
Фрактали можна одержати в результаті перетворень подібності – повороту зі стиском/розтягом. Поворот зі стиском – це добуток перетворень повороту та стиску (порядок не має значення). Розтягування/стиск відносно початку координат (центральне перетворення) задається формулами x´= cx, y´= cy, а відносно точки (х0, у0) – формулами
x´= c(x – х0) + х0, y´= c(y – y0) + y0.
При c > 1 маємо перетворення розтягування, при |c| < 1 – перетворення стиску (для фракталів, як правило, |c| < 1). При с = –1 – дзеркальне відображення (поворот на 180°).
Перетворення поворот-розтяг відносно початку координат має вигляд x´= ax – by, y´= by + ax, а відносно довільної точки:
190
