
- •1.Понятие взаимной информации
- •3.Информация в непрерывных сигналах, дифференциальная энтропия
- •4.Понятие пропускной способности канала святи
- •5.Пропускная способность непрерывного канала связи
- •6.Информация в непрерывных сообщениях, эпсилон-ентропия
- •3. - Среднее значение квадрат.Отклонения (теор.Управл и связи)
- •7.Кодирование как представления информации в цифровом виде
- •8.Назначение кодирования в системах связи
- •9.Параметры кодовых последовательностей
- •10.Классификация кодов
- •11.Понятие эффективного кодирования.
- •1Часть Теоремы Шеннона о кодировании.
- •12.Кодирование по методу Шеннона-Фано.
- •13.Кодирование по методу Хаффмана
- •14.Теорема Шеннона о кодировании для канала с помехами
- •15.Принципы помехоустойчивости кодирования
- •16.Теоремы об обнаруживающих и исправляющих способностях кодов
- •17.Представление кодовых последовательностей, передаваемыхтелекоммуникационными каналами связи
- •18.Требования к кодовым последовательностям, передаваемых телекоммуникационными каналами связи
- •19.Представление кодовых последовательностей в nrz-коде.
- •20.Предоставление кодовых последовательностей в
- •21.Представление кодовых последовательностей в биполярном импульсном коде.
- •22.Представление кодовых последовательностей в манчестерском коде.
- •23.Понятие о скремблировании. Простейший алгоритм скремблирования
- •24.Прием дискретных сообщений как статистическая задача.
- •28.Понятие критерия принятия решений при приеме дискретных сигналов. Критерий идеального наблюдателя, критерий минимума среднего риска, Критерий Неймана-Пирсона
- •30.Оптимальные алгоритмы приема при полностью известных сигналах. Оптимальный приемник на «вычитателях».
- •31.Оптимальные алгоритмы приема при полностью известных сигналах. Оптимальный приемник на корреляторах
- •30-Б.Пот.Пом.При изв.Наб.Сиг.Пост.З-чи и получ.Выр-я для вер.Ош. Приема.
- •32.Потенциальная помехоустойчивость при известном наборе сигналов.
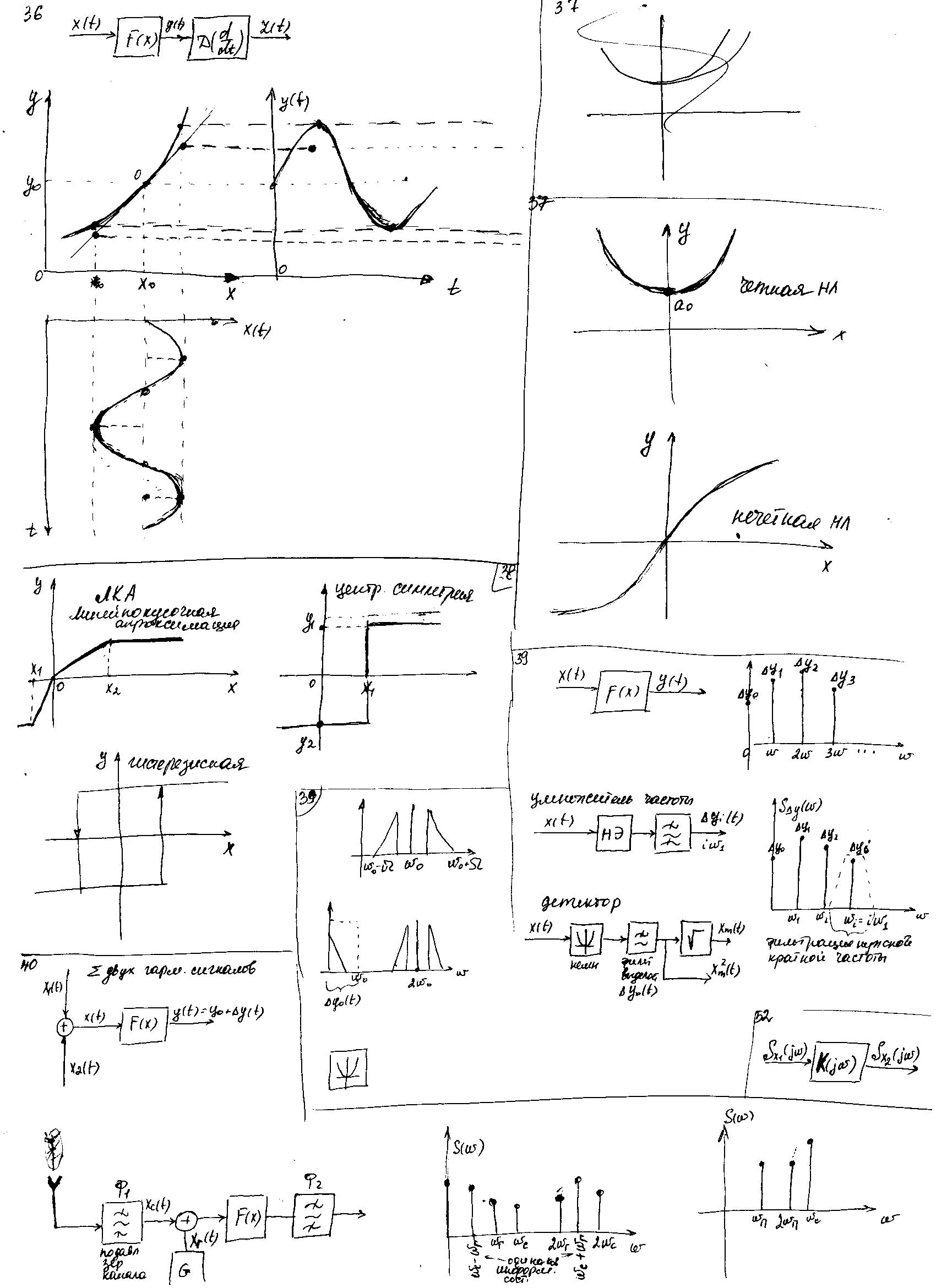
- •36. Понятие нелинейного звена и его структура.
- •37. Статические хар-ки нелинейных звеньев и их классификация: гладкие нелинейности.
- •38.Татические хар-ки нелинейных звеньев и их классификация: существенные нелинейности.
- •39. Преобразование гармонического сигнала гладкой нл-ю общего вида: умножитель частоты, детектор огибающей.
- •40. Преобразование нелинейности общего вида суммы двух гармонических сигналов: комбинационные компоненты второго порядка, смеситель на не линейность
- •41. Преобразование нелинейностью общего вида суммы двух гармонических сигналов: интермодуляционные составляющие третьего порядка.
- •42. Преобразование закона распределения случайного сигнала однозначной гладкой не линейностью
- •43. Преобразование закона распределения случайного сигнала неоднозначной гладкой нелинейностью.
- •44. Преобразование закона распределения случайного сигнала существенной нелинейностью: пример применения метода.
- •65. Помехи и шумы передатчиков
- •66. Шумы приемников: тепловые шумы элементов
- •70.Приведение шумов звена к его входу. Шумовая температура
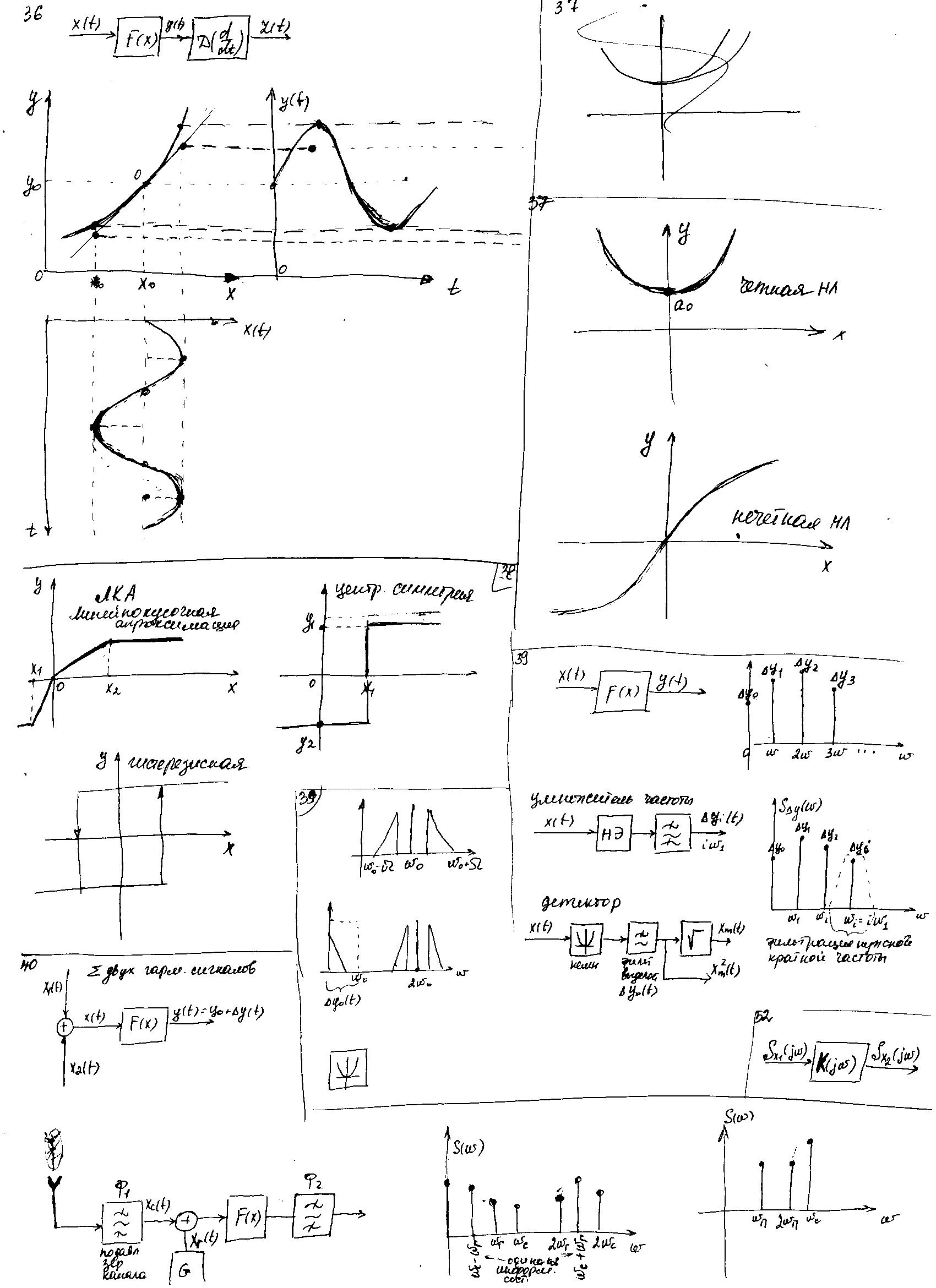
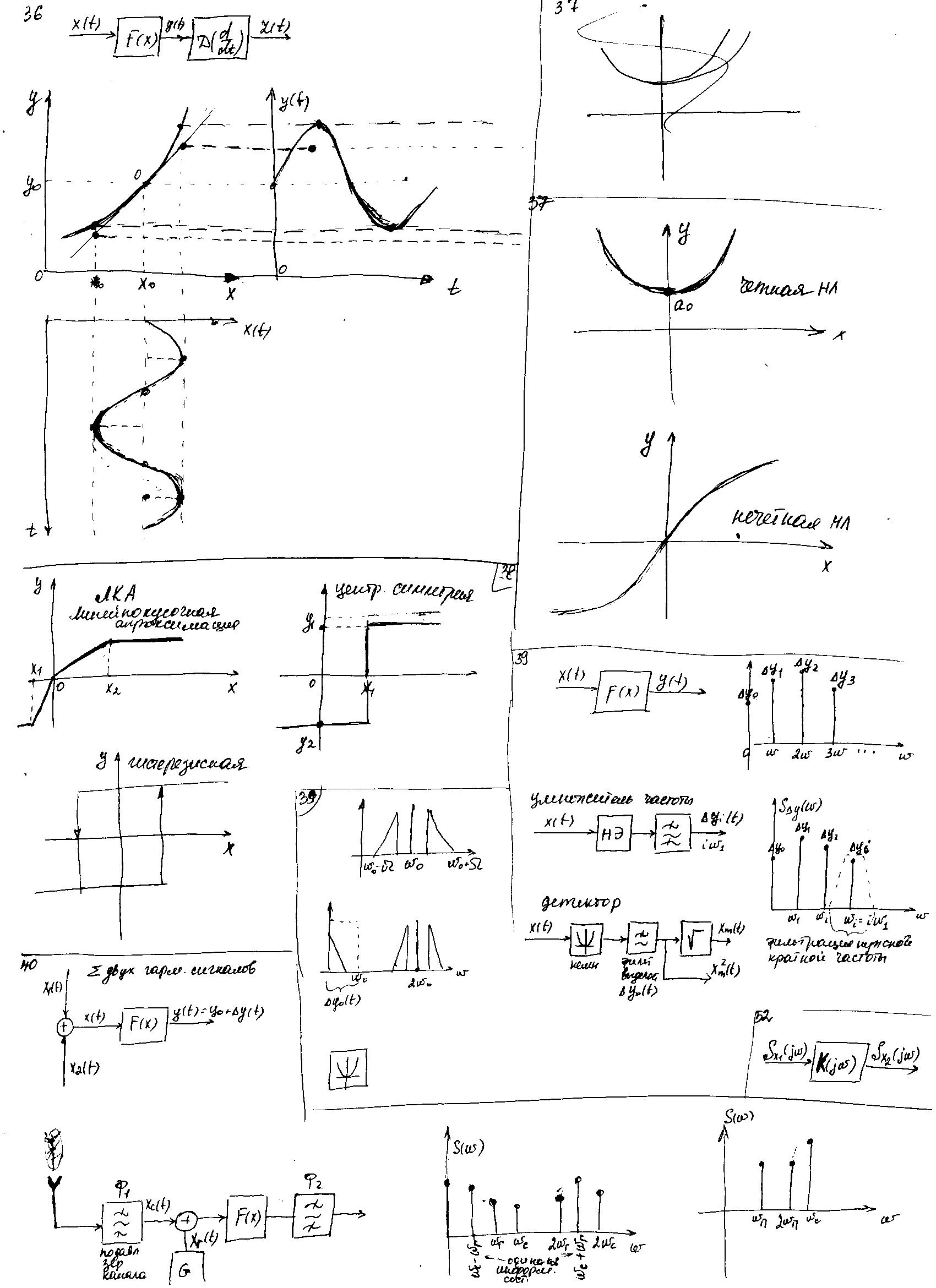
37. Статические хар-ки нелинейных звеньев и их классификация: гладкие нелинейности.
Четная НЛ-симметрична относительно оси ординат.
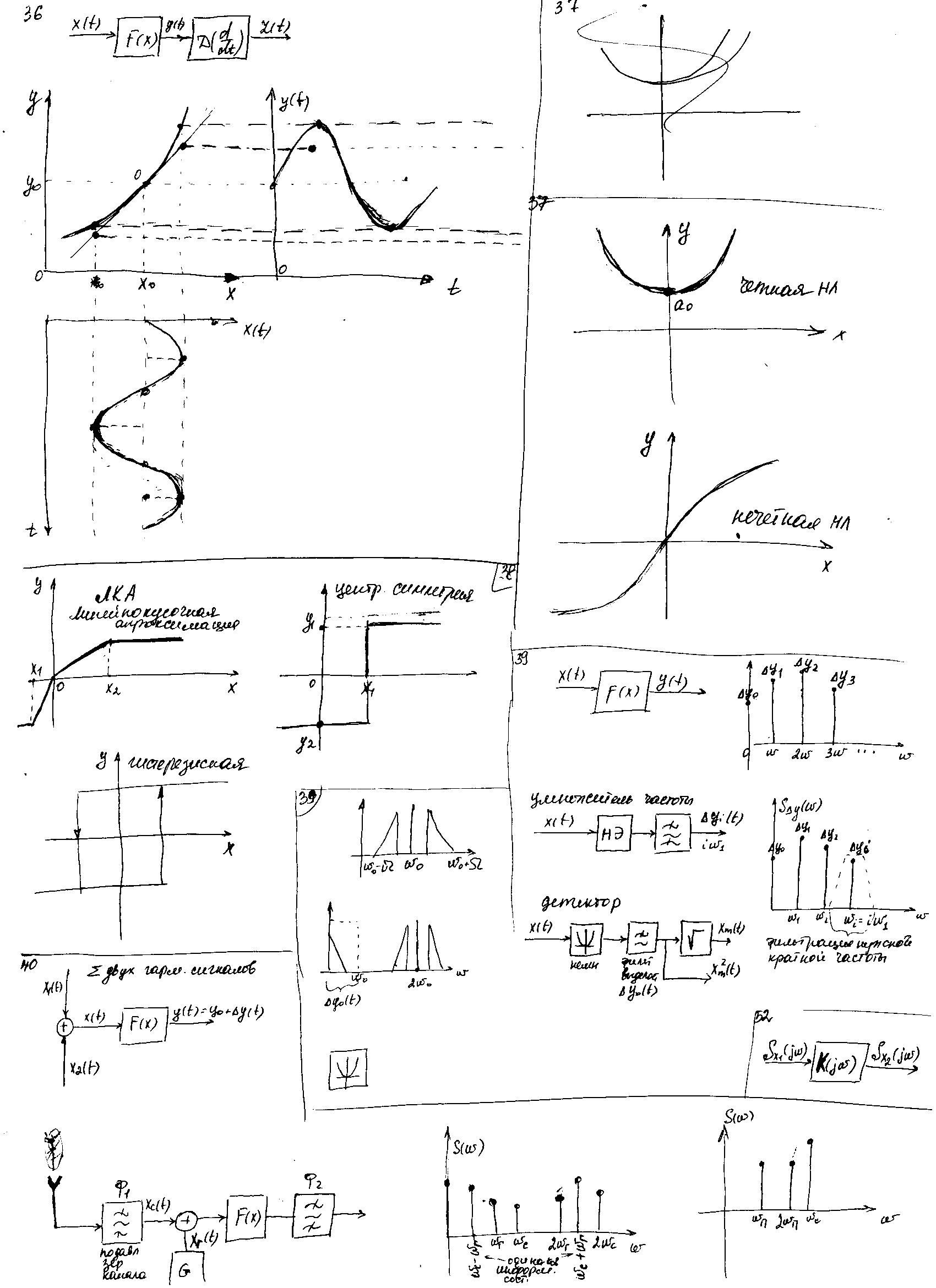
Нечетная НЛ – центральная симметрия
![]()
![]()
![]()
т.е. в разложении только четные степени
![]()
![]() ,
,
38.Татические хар-ки нелинейных звеньев и их классификация: существенные нелинейности.
1.Есть точки излома. Данный метод описания, основанный на методе кусочно-линейной аппроксимации, позволяет решать сложные динамические задачи методом «сшивки».


2.Центральная симметрия. Функция однозначная.
![]()
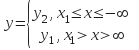
3. гистерезисная характеристика. Характеристики неоднозначны

![]()
39. Преобразование гармонического сигнала гладкой нл-ю общего вида: умножитель частоты, детектор огибающей.
![]()
![]() Если
гармонич.сигнал проходит через НЛ, то
получат: кратные высшие гармоники. УПС
имеют св.-ва
Если
гармонич.сигнал проходит через НЛ, то
получат: кратные высшие гармоники. УПС
имеют св.-ва![]() синусоиде,
сигналы м.представлять как сумму
синусоид.
синусоиде,
сигналы м.представлять как сумму
синусоид.

- 2-е составляющие: const и гармоника удвоенной частоты. !!! отсутствует первая начальная гармоника .
![]() -
две составляющие: начальная гармоника
и утроенная гармоника.
-
две составляющие: начальная гармоника
и утроенная гармоника.
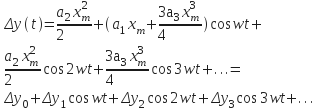
Спектр
выходного сигнала ![]() :
:
 Нелинейность
общего вида формирует в вых. сигнале
составляющие кратных частот. F(x)
– общего вида
Нелинейность
общего вида формирует в вых. сигнале
составляющие кратных частот. F(x)
– общего вида
39.ОБРАТНАЯ СТОРОНА
![]()
![]()
![]()
Для максимизации КПД необх.подбирать спец-ые видыF(x) нелинейности

Преобразование гарм.сигнала четной НЛ. Детектор огибающей.
![]()
![]() Для
узкополосного канала амплитуда огибающей
меняется медленно.
Для
узкополосного канала амплитуда огибающей
меняется медленно.
![]()
![]()
![]() .
.
![]() Прох-е
через
Прох-е
через
![]()
![]()
40. Преобразование нелинейности общего вида суммы двух гармонических сигналов: комбинационные компоненты второго порядка, смеситель на не линейность

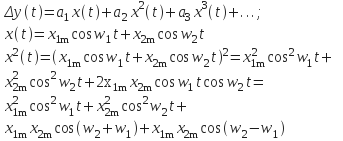
Квадратичный
член формирует доп.составляющие с
частотой ![]() и
и ![]() -
инф.сигнал опред.выделение из пост.сост.
2-й гармоники
-
инф.сигнал опред.выделение из пост.сост.
2-й гармоники
Реализация смесителя на квадратичной НЛ.

0 ОБРАТНАЯ СТОРОНА
Фильтр при селекторе-подавл.верт.канал G-гетеродин.
![]() -
сигнал с антены
-
сигнал с антены
![]() -
сигнал гетеродина, гармон.
-
сигнал гетеродина, гармон.

Пост.составл.не
интересуют, инф.сост. интересуют ![]() и
и![]() -
несут одинок.информацию.
-
несут одинок.информацию.

Обычно
фильтр выдел. ![]() ,тк
она меньше.
,тк
она меньше.
График
отображ.w
помехи=![]() ,
которая пост.на вход приемника и
удваивается по частоте, близко к w
полезности и мб подавлен
,
которая пост.на вход приемника и
удваивается по частоте, близко к w
полезности и мб подавлен ![]() ,
которая увеличивается НЛ, увеличивая
помехи.
,
которая увеличивается НЛ, увеличивая
помехи.
41. Преобразование нелинейностью общего вида суммы двух гармонических сигналов: интермодуляционные составляющие третьего порядка.
![]()
![]() +
+![]() +
+![]() +
+![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
полезный сигнал,
-
полезный сигнал, ![]() -
помеха. Положим, что
-
помеха. Положим, что ![]()
![]() -
близки, получис следующий спектральный
анализ:
-
близки, получис следующий спектральный
анализ:
41 ОБРАТНАЯ СТОРОНА
Получим
в фильтре еще и помеху из-за не линейности.
(2![]() -
-![]() )
->
)
->![]() ,
следовательно фильтрацией не подавляется.В
выходном сигнале появляются новые
спектральные составляющие с частотами
(2ω2-ω1) , (2ω2+ω1),(2ω1-ω2),(2ω1+ω2),3ω1 и 3ω2. Т.о.
нелинейность 3-го порядка является
причиной возникновения интермодуляционных
компонент 3-го порядка, которые по
частотам близки к частоте полезного
сигнала.
,
следовательно фильтрацией не подавляется.В
выходном сигнале появляются новые
спектральные составляющие с частотами
(2ω2-ω1) , (2ω2+ω1),(2ω1-ω2),(2ω1+ω2),3ω1 и 3ω2. Т.о.
нелинейность 3-го порядка является
причиной возникновения интермодуляционных
компонент 3-го порядка, которые по
частотам близки к частоте полезного
сигнала.
Подавление этих составляющих возможно за счет уменьшения слагаемых нелинейности 3-го порядка и более высоких порядков в описании характеристики НЭ. Выбор усилителя и преобразователя элементов с малыми нелинейностями передаточной хар-ки.
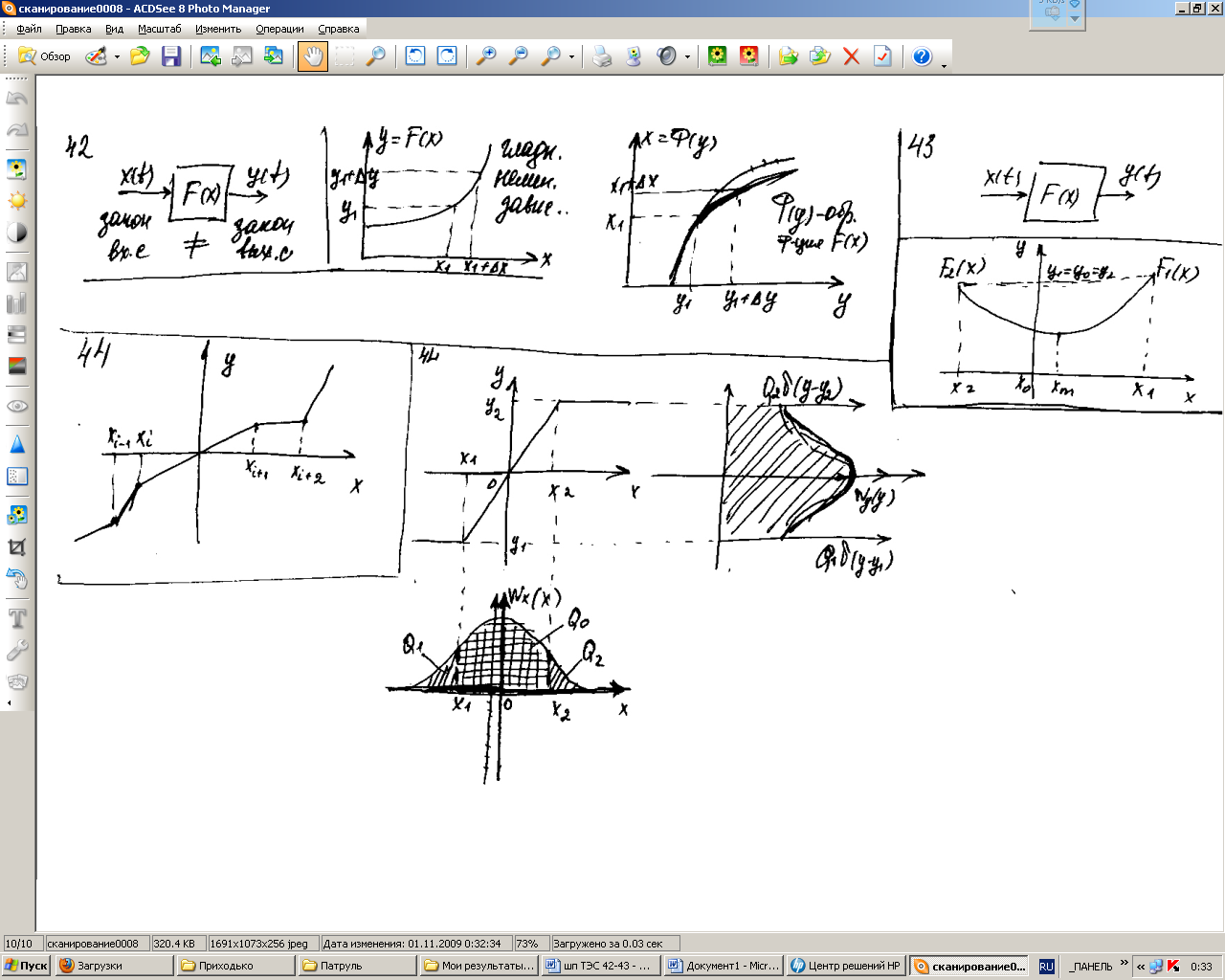
42. Преобразование закона распределения случайного сигнала однозначной гладкой не линейностью

F(x)-обозначенная
функция, ![]() ,
,
![]() ,
,
![]()
2
формы распределения: - дифференциальный
(диапазон ![]() )
и интегральный.
)
и интегральный.
Т.к.ф-ция однозначная, можем построить обратную ф-цию
Вероятность
того, что х лежит в [x1,x1+![]() ]:
]:
![]() =
=
![]() ,
тогда при
,
тогда при ![]()
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]()
