
- •1.Понятие взаимной информации
- •3.Информация в непрерывных сигналах, дифференциальная энтропия
- •4.Понятие пропускной способности канала святи
- •5.Пропускная способность непрерывного канала связи
- •6.Информация в непрерывных сообщениях, эпсилон-ентропия
- •3. - Среднее значение квадрат.Отклонения (теор.Управл и связи)
- •7.Кодирование как представления информации в цифровом виде
- •8.Назначение кодирования в системах связи
- •9.Параметры кодовых последовательностей
- •10.Классификация кодов
- •11.Понятие эффективного кодирования.
- •1Часть Теоремы Шеннона о кодировании.
- •12.Кодирование по методу Шеннона-Фано.
- •13.Кодирование по методу Хаффмана
- •14.Теорема Шеннона о кодировании для канала с помехами
- •15.Принципы помехоустойчивости кодирования
- •16.Теоремы об обнаруживающих и исправляющих способностях кодов
- •17.Представление кодовых последовательностей, передаваемыхтелекоммуникационными каналами связи
- •18.Требования к кодовым последовательностям, передаваемых телекоммуникационными каналами связи
- •19.Представление кодовых последовательностей в nrz-коде.
- •20.Предоставление кодовых последовательностей в
- •21.Представление кодовых последовательностей в биполярном импульсном коде.
- •22.Представление кодовых последовательностей в манчестерском коде.
- •23.Понятие о скремблировании. Простейший алгоритм скремблирования
- •24.Прием дискретных сообщений как статистическая задача.
- •28.Понятие критерия принятия решений при приеме дискретных сигналов. Критерий идеального наблюдателя, критерий минимума среднего риска, Критерий Неймана-Пирсона
- •30.Оптимальные алгоритмы приема при полностью известных сигналах. Оптимальный приемник на «вычитателях».
- •31.Оптимальные алгоритмы приема при полностью известных сигналах. Оптимальный приемник на корреляторах
- •30-Б.Пот.Пом.При изв.Наб.Сиг.Пост.З-чи и получ.Выр-я для вер.Ош. Приема.
- •32.Потенциальная помехоустойчивость при известном наборе сигналов.
- •36. Понятие нелинейного звена и его структура.
- •37. Статические хар-ки нелинейных звеньев и их классификация: гладкие нелинейности.
- •38.Татические хар-ки нелинейных звеньев и их классификация: существенные нелинейности.
- •39. Преобразование гармонического сигнала гладкой нл-ю общего вида: умножитель частоты, детектор огибающей.
- •40. Преобразование нелинейности общего вида суммы двух гармонических сигналов: комбинационные компоненты второго порядка, смеситель на не линейность
- •41. Преобразование нелинейностью общего вида суммы двух гармонических сигналов: интермодуляционные составляющие третьего порядка.
- •42. Преобразование закона распределения случайного сигнала однозначной гладкой не линейностью
- •43. Преобразование закона распределения случайного сигнала неоднозначной гладкой нелинейностью.
- •44. Преобразование закона распределения случайного сигнала существенной нелинейностью: пример применения метода.
- •65. Помехи и шумы передатчиков
- •66. Шумы приемников: тепловые шумы элементов
- •70.Приведение шумов звена к его входу. Шумовая температура
1.Понятие взаимной информации
Энтропия – среднее количество информации на одно сообщение, которое формируется источником.
![]()
![]() -потеря
информации
-потеря
информации
T – среднее время передачи 1 сообщения
![]() ,
,
![]()
![]()

Физический смысл:
![]() скорость
форм.источника информации
скорость
форм.источника информации![]() пердача
– фильтрация, потери, помехи
пердача
– фильтрация, потери, помехи ![]() в
процессе распространения в ЛС добавл.
Помехи (случайные, КС)
в
процессе распространения в ЛС добавл.
Помехи (случайные, КС) ![]() увеличивается
количество информации в
увеличивается
количество информации в ![]()
Взаимную информацию м. определить:
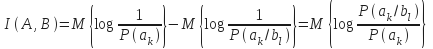
Если
воспользоваться теоремой умножения
вероятностей для взаимосвязанных
сообщений![]() ,
то
,
то
получим:
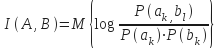 симметрич формула 2.Свойства
взаимной информации
симметрич формула 2.Свойства
взаимной информации

.
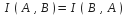 ,
откуда следует
,
откуда следует 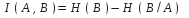
.
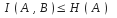 ,
т. к. существуют потери в КС.
,
т. к. существуют потери в КС.
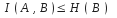 ,
т. к. существуют потери в КС.
,
т. к. существуют потери в КС.Если В=А и учитывая, что
 ,
то
,
то  ,
т.е. энтропия источника есть его
собственная информация.
,
т.е. энтропия источника есть его
собственная информация.
3.Информация в непрерывных сигналах, дифференциальная энтропия
 Закон
распределения для данного момента
времени:
Закон
распределения для данного момента
времени: ![]() .
W(s)
- плотность
распределения.
.
W(s)
- плотность
распределения.
При
![]()
![]()
![]() .
Энтропия источника генерирующего
случайную величину
.
Энтропия источника генерирующего
случайную величину
![]()
![]() Непрерывный
сигнал содержит
Непрерывный
сигнал содержит ![]() число признаков
число признаков
![]() ;
;
![]() ;
;
![]()
Работа
систем аналоговой связи : суть состоит
в том, что 1) мы интересуемся частью
информации в аналоговом сигнале (сигнал
подавляется фильтрацией),
2) изменение
информации при передаче информации
взаимная,
а не полная энтропия нас интересует,
рассматрив. приращ.
энтропии
вел-ны не будут ![]() 3)
дифференциальная энтропия – характеристика
непрерывного источника. Для непрер.случайн.
величины с
законом
изменения- интеграл от произведения
этой величины на закон распр.этой
величины.
х –
непрерывная случайная величина.
3)
дифференциальная энтропия – характеристика
непрерывного источника. Для непрер.случайн.
величины с
законом
изменения- интеграл от произведения
этой величины на закон распр.этой
величины.
х –
непрерывная случайная величина.
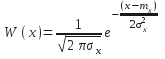
![]()
![]()
![]() Дифференц.энтропия
нормального распределения зависит от
мощности сигнала
Дифференц.энтропия
нормального распределения зависит от
мощности сигнала
![]() ;S,
U
– непрер-е
случ.величины
;S,
U
– непрер-е
случ.величины
![]() ;
;![]()
![]()
![]()
![]()
![]()
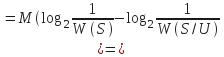
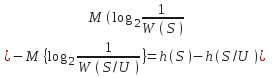
![]() в
{}усл.плотность
вероя-и
2
источ-в
в
{}усл.плотность
вероя-и
2
источ-в
4.Понятие пропускной способности канала святи

![]()
1![]() [бит/символ]
– пропускная способность потока.
[бит/символ]
– пропускная способность потока.
Пропускная способность – характеристика канала связи – экономичность информации. Экономия энергии и временных затрат на передачу.
2.
 [Бит/с]
[Бит/с]
![]()
Достигаем max С за счет скремблирования, фильтрации, переноса спектра. При этом свойства канала используется наилучшим образом.
![]() -
-![]() передачи
КС,
достигаемая за счет предварительного
преобразования
сигнала.
Экономичность
представления сигналов в этом канале,
оценивается Бит/симв
передачи
КС,
достигаемая за счет предварительного
преобразования
сигнала.
Экономичность
представления сигналов в этом канале,
оценивается Бит/симв
![]() передачи
в КС, достигаемое за счет оптимизации
временных характеристик сигналов,
оптимизации частот этих сигналов.
передачи
в КС, достигаемое за счет оптимизации
временных характеристик сигналов,
оптимизации частот этих сигналов.
Пропускная способность – некий предел к которому стремится скорость передачи. Реальные нагрузки КС< С пропускной способности канала
Способ
кодирования передачи бит как процесс
во времени. Время,
тратившееся на передачу
одного символа
– техническая скорость передачи (Бит/с).
Коэффициент
передачи =
отношению
скорости передачи
![]() к пропускной способности - для дискретных
каналов.
к пропускной способности - для дискретных
каналов.
5.Пропускная способность непрерывного канала связи
F-полоса
пропускания КС, те диапазон частот. ![]() -
интервал дискретизации.
-
интервал дискретизации.
П![]() ропускная
способность на один отсчет -
ропускная
способность на один отсчет -
![]()
![]() .Дифференциальная
энтропия – энерг характ источника,
условн.энтропия- потери в КС.
.Дифференциальная
энтропия – энерг характ источника,
условн.энтропия- потери в КС.
Пусть
![]()
![]() .
.
![]()
![]() дифференциальная
условная энтропия сообщения Z
при известном U.
дифференциальная
условная энтропия сообщения Z
при известном U.
![]() дифференциальная
энтропия на выходе КС
дифференциальная
энтропия на выходе КС
Поскольку
шум аддитивный, то ![]() ;
;
![]() дифференциальная
энтропия
дифференциальная
энтропия
![]()
![]()
Чем
шире полоса частот, тем больше информативных
параметров источника можно использовать.Чем
больше
полоса,
тем больше
пропускная способность. Cкорость
нарастания ограничена, при уменьшении
шумов мы не можем сделать их 0,
и параметры сигнала
мы не можем
сделать ![]() .
.
