5.2.3 Астигматизм та кривизна поля

Астигматизм і кривизна поля зображення відносяться до польових аберацій. Вони помітно впливають на якість зображення, викликаючи його нерізкість при великих кутових (або лінійних) полях. На відміну від коми ці дві аберації виникають при зображенні позаосьової точки предмета нескінченно вузькими (елементарними) похилими пучками.

Астигматизмполягає в тому, що зображення однієї і тої самої точки предмета нескінченно тонкими пучками променів – меридіональними та сагітальними – виходить у вигляді двох точок, які не співпадають із зображенням, утворюваним параксіальними променями (рис. 5.5).

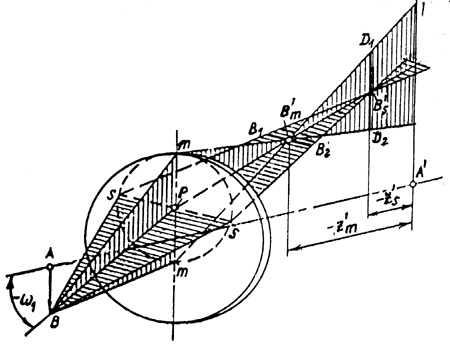
Рисунок 5.5– Зображення позаосьової точки при астигматизмі

На рис. 5.5 пучок променів, що розповсюджується з позаосьової точки В у меридіональній площині, позначений черезmm, а пучок, що розповсюджується сагітальній площині, – черезss(сагітальна площина проходить через вісь пучка перпендикулярно меридіональній площині). Віссю пучка є головний промінь, що розповсюджується з точки В та проходить через центр вхідної зіниці (точка Р). Через те, що кривизна оптичних поверхонь для меридіонального та сагітального пучків виявляється різною, проміні меридіонального пучка збираються в точці В′m, а сагітального - в точці В′s, які розташовані на відстаняхz'mтаz'sвід площини Гаусса (площини параксіального зображення). Обидві точки лежать на головному промені. Відстань по головному променю між точками В′m та В′s називаєтьсяастигматичною різницею, абоастигматизмом. Зазвичай астигматизм вимірюють по оптичній осі різницею відрізківz'sтаz'm, тобто визначають якz's-z'm.

Якщо розглянути весь конічний пучок променів, що виходить з точки В, то зображення точкиВ, утворюване меридіональними променями, буде виходити у вигляді горизонтальної лінії В1В2, що лежить в сагітальній площині. Аналогічно, зображення точки В сагітальними променями виходить у вигляді вертикальної лінії D1D2, що лежить в меридіональній площині. У площині параксіального зображення пляма розсіювання має форму еліпса; в перетині, що проходить через точку В', – форму кола. Між точками В′m та В′s фігури розсіювання мають вигляд еліпсів з різною орієнтацією осей.

У випадку протяжного об’єкта необхідно розглядати сукупність точок цього об’єкта, кожна з яких зображується астигматичними пучками променів. Якщо об’єктом є відрізок прямої АВ, розташований у меридіональній площині, то кожній точці цього відрізка буде відповідати меридіональне та сагітальне зображення (рис. 5.6). З’єднуючи отримані точки, одержимо криві у'mтау's, які є відповідно меридіональним та сагітальним зображенням відрізка АВ. Якщо ці криві обертати навколо оптичної осі, то отримаємо астигматичні поверхні обертання, які доторкаються площини ідеального зображення в точці А'. Так виникає інша аберація –кривизна поля зображення. Кривизна поля зображення проявляється в тому, що найкраще зображення виходить на викривленій поверхні, а не в площині.

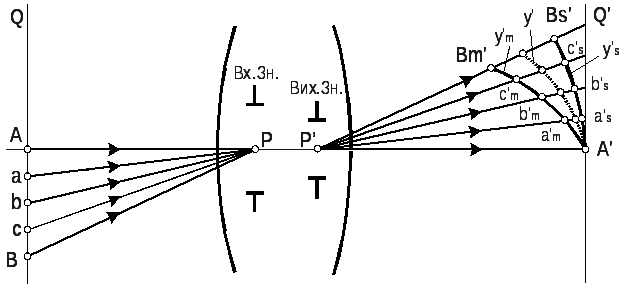
Рисунок 5.6– Зображення відрізка, утворюване астигматичними пучками

Між кривими зображень у'mтау'sпроходить середня крива зображенняу'. На поверхні зображення, яка утворюється при обертанні кривоїу' навколо оптичної осі, кожна точка відрізка АВ зображується у вигляді кружка вірної форми. На цій поверхні кривизна поля зображення має середнє значення.

Отже, наявність в оптичній системі аберацій астигматизму та кривизни поля зображення при умові, що зображення проекцується на площину, веде до нерізкого зображення точок. Ця нерізкість збільшується по мірі віддалення точки від оптичної осі. Відзначимо характерні особливості зображення, створюваного системою, що має астигматизм, для випадку, коли об’єктом є двовимірна фігура. Оптична система, що має астигматизм, не може одночасно дати різке зображення горизонтальних і вертикальних ліній. Елементарні меридіональні пучки зображують кожну точку у вигляді ліній, перпендикулярних до цих меридіональних площин. Елементарні відрізки меридіональних зображень, накладаючись одне на одне, дають різке зображення кола. Зображення точок, що належать радіусам, будуть при цьому виходити у вигляді елементарних ліній, перпендикулярних до радіусів. Довжина цих елементарних відрізків не є однаковою і збільшується по мірі віддалення від оптичної осі (рис. 5.7 б).

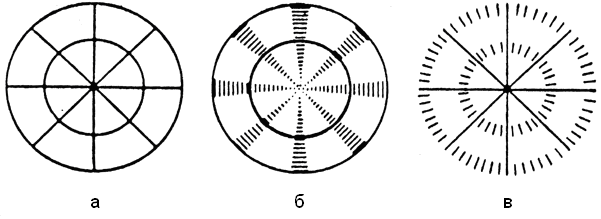
Рисунок 5.7– Зображення радіальних ліній і концентричних кіл астигматичними пучками

Елементарні сагітальні пучки будуть відображати кожну точку об’єкта у вигляді ліній, перпендикулярних до по різному орієнтованих сагітальних площин. У результаті зображення радіусів виходять не викривленими, а зображення кіл утворюються сукупністю елементарних радіальних відрізків, довжина яких збільшується по мірі віддалення від оптичної осі (рис. 5.7 в).

Астигматизм та кривизну поля зображення оптичної системи зазвичай характеризують величинами z'mтаz's(див. вище), які зводяться до таблиць та ілюструються графіками. Ці таблиці та графіки відображають залежністьz'mтаz'sвід кутів, що утворюються з оптичною віссю головними променями, які розповсюджуються з різних точок предмета, або залежністьz'mтаz's від лінійного розміру предмета.

Оптичні системи з виправленим астигматизмом і кривизною поля зображення називають анастигматами. В таких системах астигматизм та кривизна поля зображення практично повністю виправляється для деякого кута поля та мають допустимі значення у межах усього поля оптичної системи.