Контрольні питання

1. Чи може реальна оптична система давати ідеальне зображення, тобто не порушувати гомоцентричності пучків променів? Якщо так, то за яких умов?

2. Які промені називаються параксіальними? Що називається параксіальною областю оптичної системи?

3. Чим можна пояснити, що промені, які падають під різними кутами на сферичну заломлювану поверхню, після заломлення на ній перетинаються в різних точках?

4. Чому параксіальні промені після заломлення на сферичній поверхні перетинаються в одній точці?

5. Що дозволяє знайти нульовий інваріант Аббе? Як використовуючи нульовий інваріант Аббе знайти фокусну відстань сферичної заломлюваної поверхні?

6. Яким чином може бути знайдений радіус кривизни сферичної заломлюваної поверхні для забезпечення необхідного ходу променя?

7. Який промінь називається нульовим?

8. Яким чином можуть бути можуть бути визначені фокусні відстані сферичної лінзи, якщо відомі її конструктивні параметри? До конструктивних параметрів лінзи належать радіуси кривизни заломлюваних поверхонь, показник заломлення матеріалу лінзи, товщина лінзи по осі.

9. Охарактеризуйте передню та задню фокусні відстані сферичної лінзи, розташованої у повітрі та на поверхні води (у воду занурена тільки перша заломлювана поверхня).

3Матрична теорія параксіальної оптики

3.1 Перетворення координат променів оптичною системою. Матриця перетворення

Основна дія оптичної системи полягає у зміні ходу променів, що описується перетвореннями двох параметрів - лінійної і кутової координат променя. Ці перетворення найбільш зручно описувати за допомогою апарату матричної оптики. Матриця перетворення повністю описує розповсюдження променів через оптичну систему.

Параметри променя у просторах предметів та зображень можуть бути поставлені тільки в тому випадку, якщо вибрані опорні площини (ОП). Опорна площина–це деяка довільно обрана площина, перпендикулярна оптичній осі. Опорні площини в просторіпредметів і зображень вибираються з міркувань зручності і можуть бути або сполученими, або ні.

На рис. 3.1 показана лінійна yта кутоваαкоординати променя.

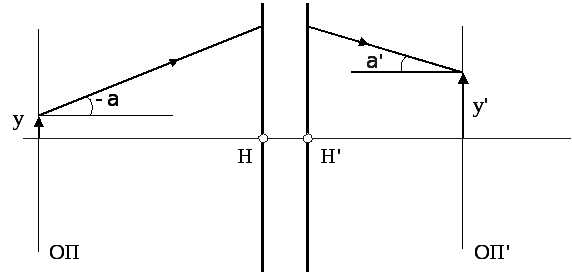
Рисунок 3.9 – Координати променя

Замість кута αчасто використовують направляючий косинус Yоптичного променевого вектора:

. (3.32)

де β– кут між променем та віссю ОY.

З врахуванням того, що розглядуваний промінь є параксіальним, вираз (3.1) можна записати у вигляді:

.

Добуток n · αназиваєтьсяприведеним кутом.

Для променів, що розповсюджуються у меридіональній площині, направляючий косинус Х= 0. Отже у параксіальній оптиці промінь, що розповсюджуються у меридіональній площині, може бути однозначно визначений через лінійну координатуута кутову координатуY= -n · α:

. (3.33)

Аналогічно параксіальний промінь у просторі зображень описується лінійною координатою у'та кутовою координатуY'= -n' · α':

. (3.34)

Дія оптичної системи полягає у перетворенні координат:

.

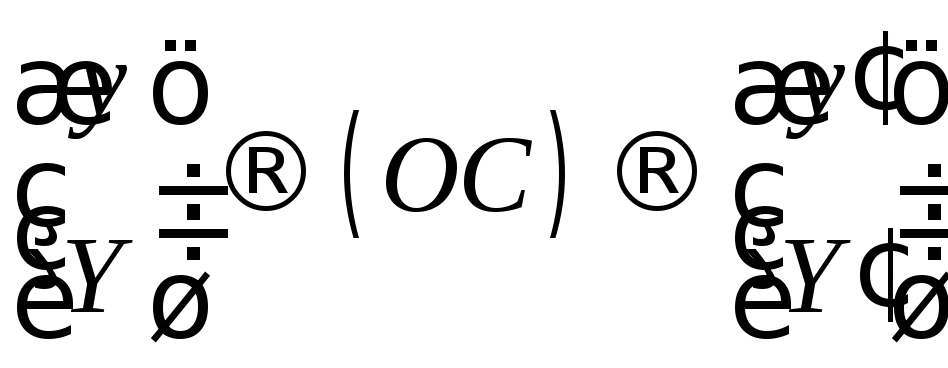Розкладемо вихідні координати променя у ряд:

.

.

Якщо оптична система є центрованою, то a₀ = b₀ = 0. Усіма членами ряду, починаючи зa₃таb₃, можна знехтувати, оскільки вони прямують до нуля на порядок швидше, ніж попередні. Таким чином для ідеальної оптичної системи:

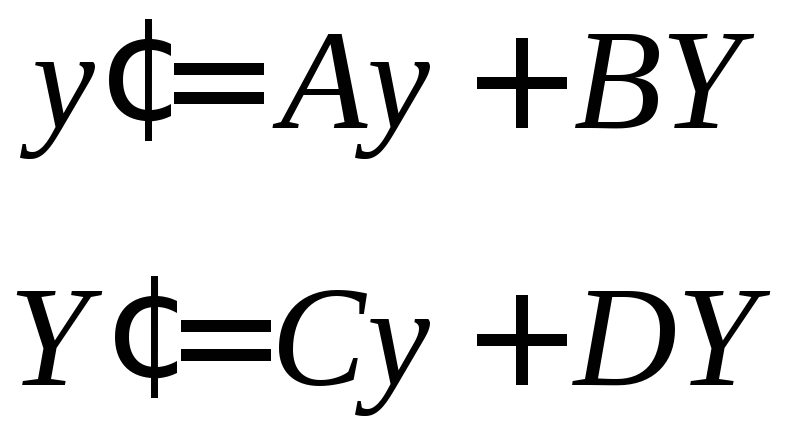. (3.35)

Вираз (3.4), який описує перетворення лінійної та кутової координат променя, можна записати у матричній формі:

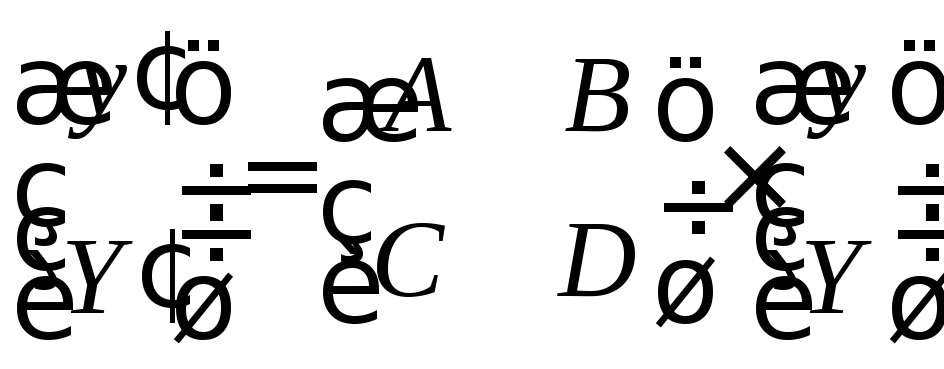. (3.36)

Матриця

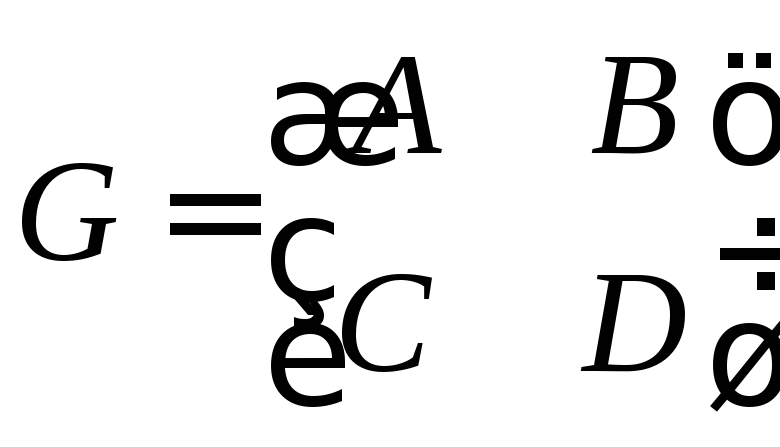(3.37)

у виразі (3.5) називається матрицею перетворення променівабогауссовою матрицею. Усі властивості ідеальної оптичної системи можуть бути описані цією матрицею.

Вираз (3.5) можна переписати у вигляді:

, (3.38)

де b– вектор стовпець вхідних координат променя;

b'– вектор стовпець вихідних координат променя.

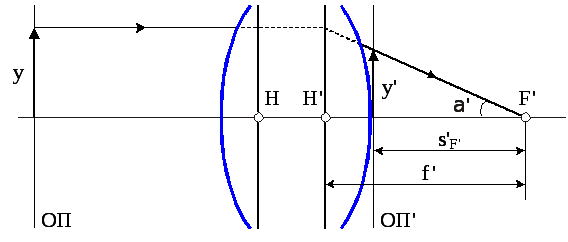
Рисунок 3.10 – Схема для знаходження елементів АтаСматриці перетворення

Для знаходження геометричного сенсу елементів матриці перетворення G, розглянемо промінь з координатамиу= 1 таY= 0 (рис. 3.2). Підставивши ці координати у вираз (3.4), отримаємо:

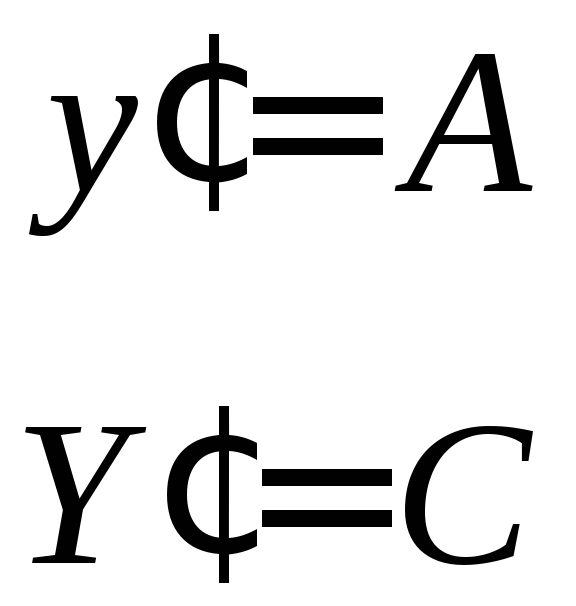. (3.39)

Знайдемо значення у'таY'= -n' · α', використовуючи рис. 3.2 та враховуючи, що для параксіальних променівtgα ≈ α:

;

.

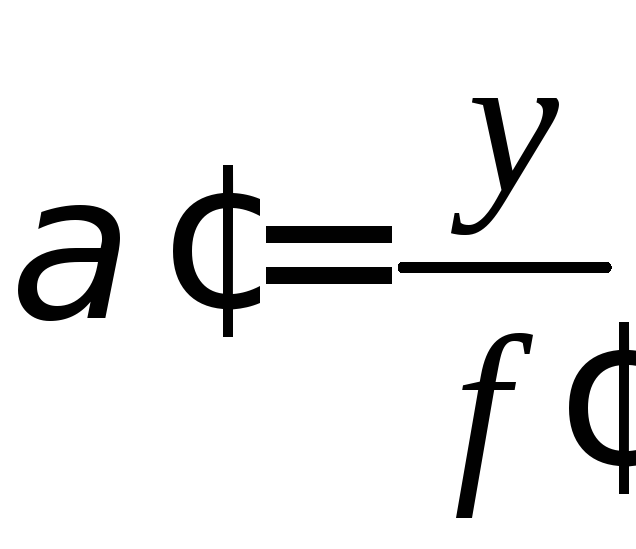Враховуючи, що у= 1, дляу'таY'= -n'·α' остаточно отримаємо:

. (3.40)

Порівнюючи вирази (3.8) та (3.9), для елементів АтаСматриці перетворення одержимо:

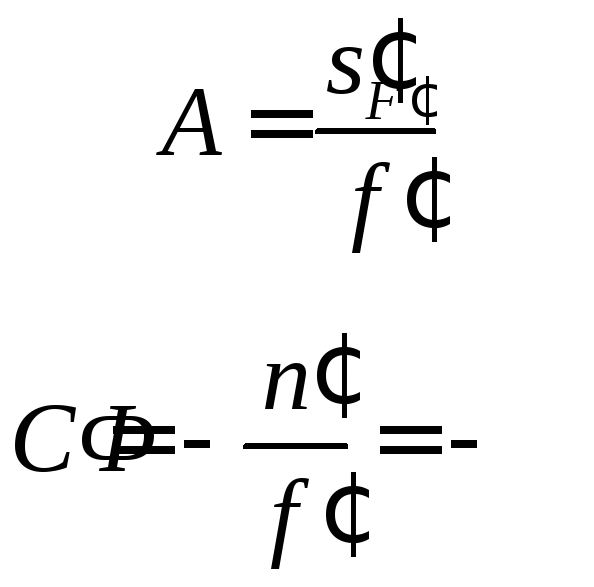. (3.41)

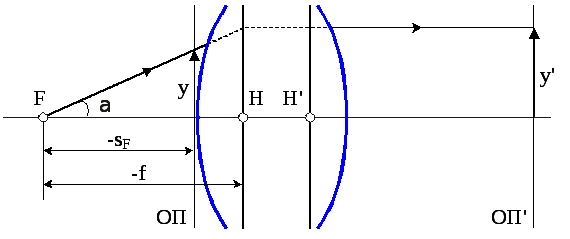
Рисунок 3.11 – Схема для знаходження елементів BтаDматриці перетворення

Для знаходження елементів BтаDрозглянемо промінь з вхідною координатоюY= 1 і вихідною координатоюY'= 0 (рис. 3.3). Підставивши ці координати у вираз (3.4), отримаємо:

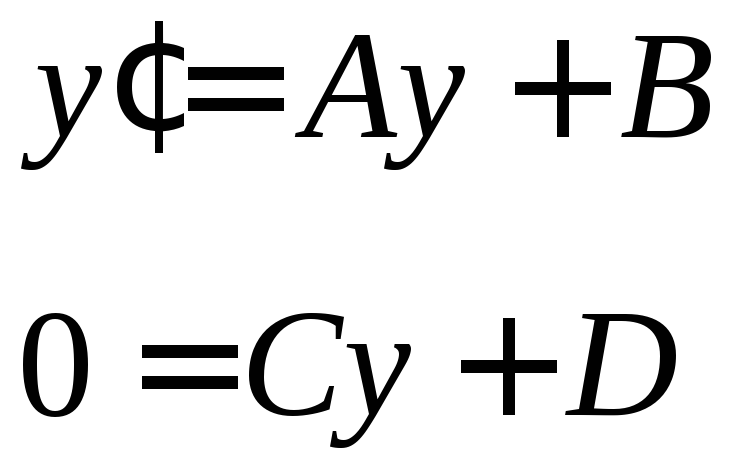(3.42)

З рис. 3.3 видно, що:

;

.

Оскільки було прийнято, що Y= 1, тоα = -(1/n). Тоді остаточно отримаємо:

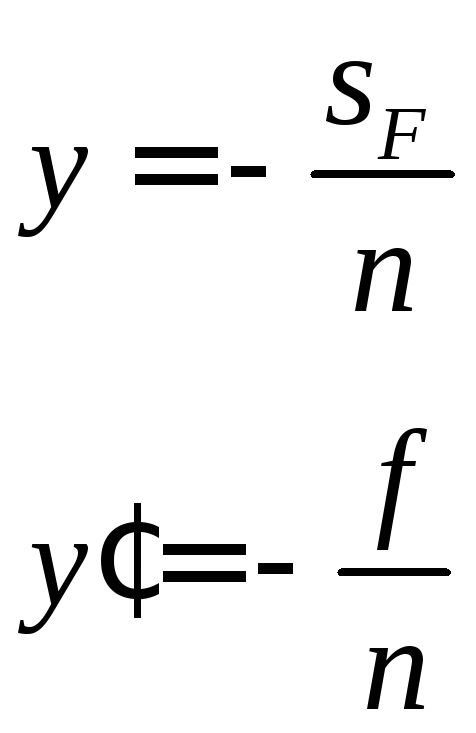. (3.43)

Порівнюючи вирази (3.11) та (3.12), для елементів BтаDматриці перетворення одержимо:

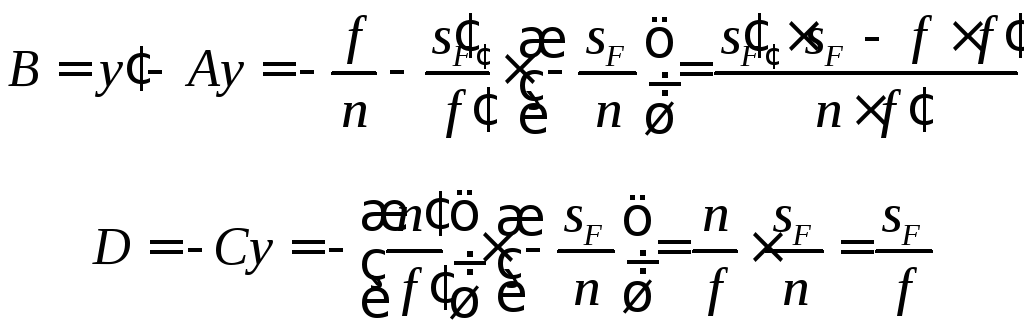. (3.44)

Таким чином матриця перетворень буде мати вигляд:

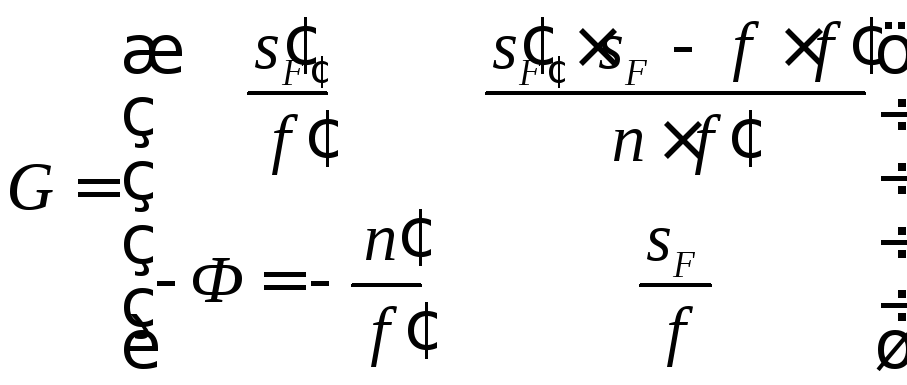(3.45)

Елемент Сматриці залежить тільки від параметрів оптичної системи, а елементиА,BтаDще й від вибору опорних площин. Усі елементи матриці перетворення у загальному випадку відрізняються від нуля. Для випадку, коли опорні площини є сполученими,у' =β·у, деβ– лінійне збільшення. Тоді, як випливає з виразу (3.4) дляу', елементBматриці перетворення у випадку сполучених площин дорівнює 0.

Визначник матриці перетворення (3.14) будь-якої оптичної системи дорівнює одиниці. Зворотна матриця перетворення, яка описує перетворення вихідних координат променя у вхідні, має вигляд:

.

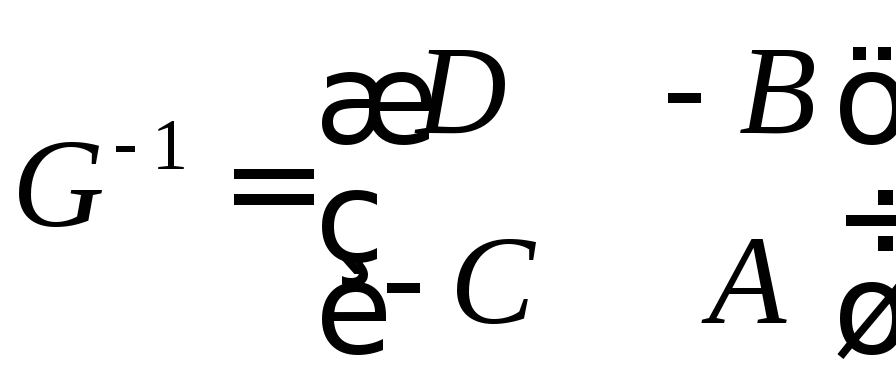Існує два основних види матриці перетворення, що описують два простих перетворення – перенесення променя у вільному просторі та заломлення променя на заломлюваній поверхні.

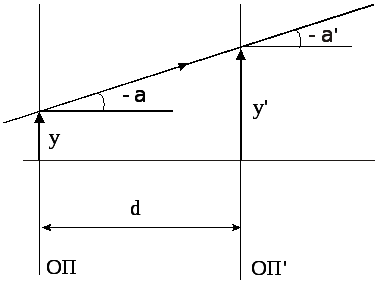
Рисунок 3.12 – Перенесення променя

При перенесенні променя змінюється тільки його лінійна координата. Як видно з рис. 3.4

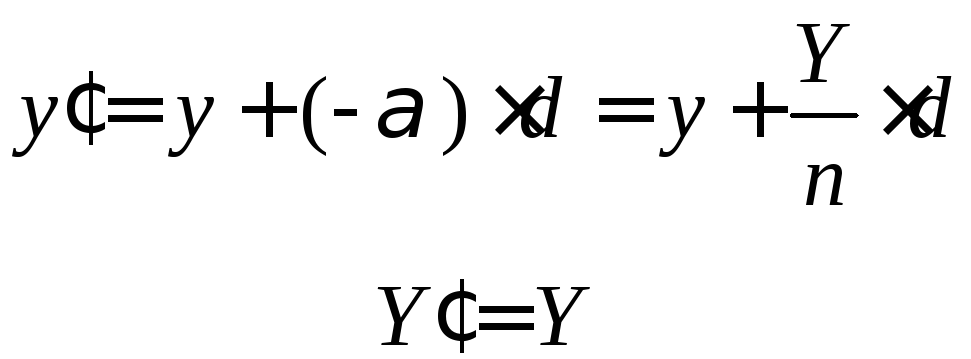(3.46)

Порівнюючи (3.15) та (3.4), визначаємо, що А= 1,B=d/n, С= 0, аD= 1. Отже матриця перетворенняG, яка у цьому випадку має сенс матриці перенесенняТ, буде мати вигляд:

(3.47)

Частка d/nназиваєтьсяприведеною відстаннюміж опорними площинами абоприведеною товщиною оптичного проміжку з показником заломлення n.

Для отримання матриці заломлення, сумістимо опорні площини з головними площинами (рис. 3.5). У цьому випадку у' =у, і тому при заломленні змінюється тільки кутова координата променя. Оскількиу' =у, то, як випливає з виразу (3.4) дляу',А= 1, аB= 0. Визначник матриці перетворенняdetG = A ·D – B ·C = 1, і томуD= 1. ЕлементCзалишається незмінним.

Рисунок 3.13 – Заломлення променя

Матриця перетворення G, яка у цьому випадку має сенс матриці заломленняRі описує заломлення променя оптичною системою, буде мати вигляд:

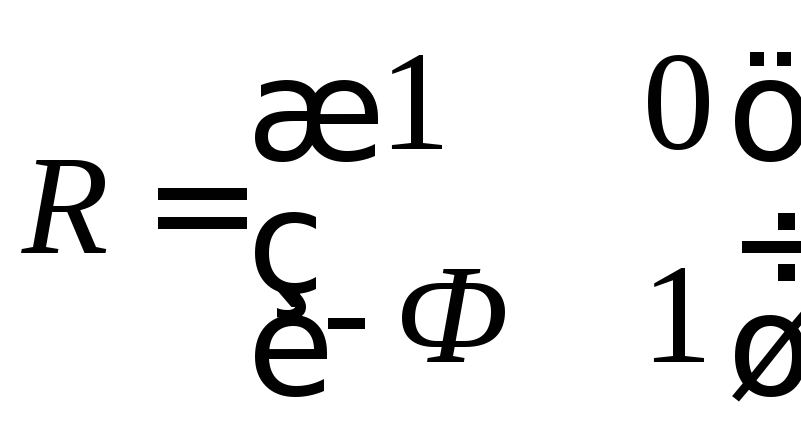. (3.48)

На основі виразу (2.27), що визначає оптичну силу сферичної заломлюваної поверхні, матриця заломлення однієї сферичної поверхні (рис. 2.11) буде мати вигляд:

.

При відбиванні промінь повертається у те саме середовище, розповсюджуючись у зворотному напрямі. Тому можна розглядати, що n′ = -n. Тоді матриця заломлення сферичної дзеркальної поверхні запишеться у вигляді:

.
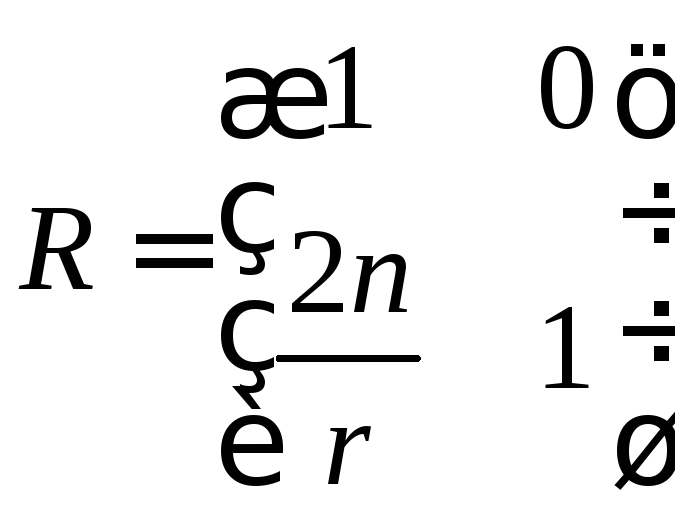