2.6 Параксіальна область оптичної системи. Параксіальні і нульові промені

Реальні оптичні системи, що складаються зі сферичних і плоских заломлюваних і відбивальних поверхонь, у загальному випадку не дають стигматичних зображень, тобто не задовольняють положенням ідеальної оптичної системи. Замість точкових зображень утворюються кола розсіювання. Гомоцентричність пучків променів зберігається тільки за умови, що кути та, утворені реальними променями з оптичною віссю та нормалями до заломлюваних і відбивальних поверхонь, нескінченно малі.

Промені, що утворюють малі кути і' оптичною віссю та малі кутиі' з нормаллю до заломлюваної поверхні, називаютьпараксіальними променями, а область навколо оптичної осі, всередині якої поширюються ці промені, -параксіальною областю.

Розглянемо заломлення параксіальних променів сферичною поверхнею (рис. 2.11).

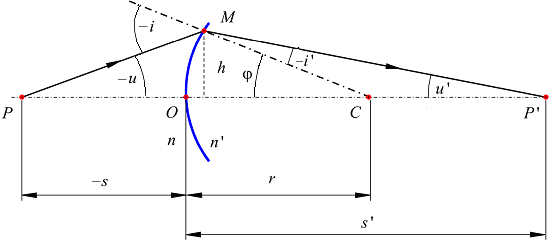
Рисунок 2.7 – Заломлення параксіальних променів сферичною поверхнею

Для нескінченно малих кутів синуси та тангенси кутів можуть бути замінені самими кутами, тобто якщо 0, то sin≈ tg≈. Тоді закон заломлення (1.4) для параксіальних променів запишеться у вигляді:

. (2.19)

Оскільки кути ітаφє зовнішніми кутами трикутників РМС та Р′ МС, то:

, (2.20)

а

. (2.21)

З рис. 2.7видно, що

,

,

.

З врахуванням записаних співвідношень, вирази (2.20) та (2.21) запишуться у вигляді:

,

.

Підставляючи отриманні вирази у закон заломлення для параксіальних променів (2.19) та скоротивши на h, отримаємо:

. (2.26)

Отриманий вираз називається нульовим інваріантом Аббе.

У вираз (2.22) не входять кути, тому будь-який параксіальний промінь, що вийшов з осьової точки Р, після заломлення на сферичні поверхні буде перетинати оптичну вісь у точці Р′.

Нульовий інваріант Аббе зручно записати у вигляді:

. (2.27)

Якщо r∞, то сферична поверхня перетворюється у плоску. Тоді на основі виразу (2.23) для заломлення параксіальних променів на плоскій поверхні можна записати:

. (2.24)

При відбиванні промінь повертається у те саме середовище, тому n′ =n. Враховуючи це та те, що при відбиванніsтаs′ будуть мати однакові знаки, на основі виразів (2.23) та (2.24) запишемо вирази для відбивання параксіальних променів на сферичній та плоскій поверхні:

, (2.25)

. (2.26)

Співвідношення (2.23)(2.26) називаютьрівняннями параксіальних променів. Використовуючи їх можна розрахувати хід параксіальних променів через послідовність оптичних поверхонь.

З виразу (2.23) можна знайди фокусну відстань для сферичної заломлюваної поверхні. Справді, якщо s∞, тоs′f′. Тоді з виразу (2.23) для оптичної сили сферичної заломлюваної поверхні маємо:

. (2.27)

При розрахунках ходу параксіальних променів через велику кількість оптичних поверхонь замість виразів (2.23)(2.26) зручніше користуватися формулами кутів та висот. З врахуванням виразу (2.27) та того, що кути, які утворюються параксіальними променями з оптичною віссю, прийнято позначати через, формули кутів (2.17) та висот (2.18) для параксіальних променів набудуть вигляду:

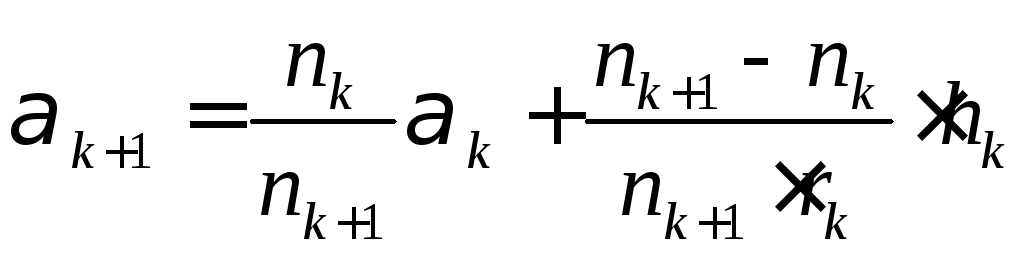, (2.28)

. (2.29)

З виразу (2.28) можна отримати формулу для радіуса кривизни сферичної поверхні при необхідному ході променя:

.

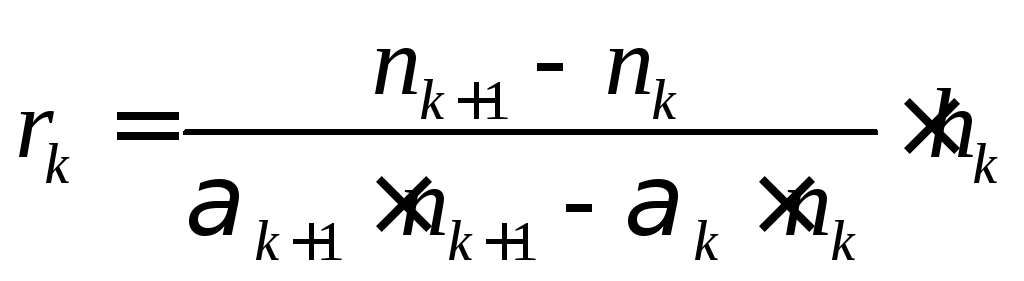Для зручності виконання розрахунків вводиться поняття нульових променів. Нульовим променем називають фіктивний промінь, що заломлюється (відбивається) на поверхнях так само, як і параксіальний, але утворює кінцеві кути з оптичною віссю та нормалями до заломлюючих поверхонь.

Шляхом розрахунку за виразами (2.28) та (2.29) ходу нульового променя через оптичну систему визначають фокусні відстані і фокальні відрізки, а також положення зображення та лінійне збільшення системи для випадку, коли предмет знаходиться на кінцевій відстані.

Розглянемо використання формул (2.28) та (2.29) для знаходження фокусної відстані сферичної лінзи (рис. 2.8) при умові, що показник заломлення середовища перед лінзою – n1, матеріалу лінзи –n2 та середовища після лінзи –n3. Через задній фокус лінзи проходять промені, які перед лінзою розповсюджуються паралельно оптичній осі, тобто які утворюють нульовий кут з оптичною віссю.

Рисунок 2.8 – Схема для знаходження фокусної відстані сферичної лінзи

Послідовно використовуючи вирази (2.28) та (2.29) з врахуванням того, щоα1 = 0, отримаємо:

;

;

.

При знаходженні висоти h2 падіння променя на другу заломлювану поверхню було прийнято, що, оскільки параксіальний промінь розповсюджується на малій відстані від оптичної осі, відстань вздовж оптичної осі між точками А та В дорівнює відстані між точками О та О' і дорівнює товщині лінзи по осіd.

Остаточно для кута α3, який утворюється вихідним променем з оптичною віссю, будемо мати:

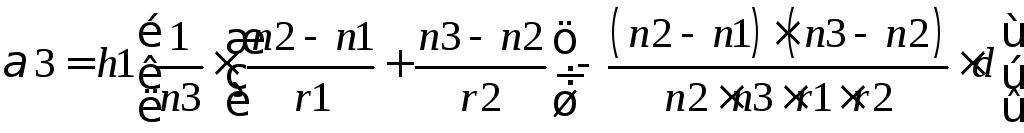. (2.28)

З іншого боку (див. рис. 2.8)

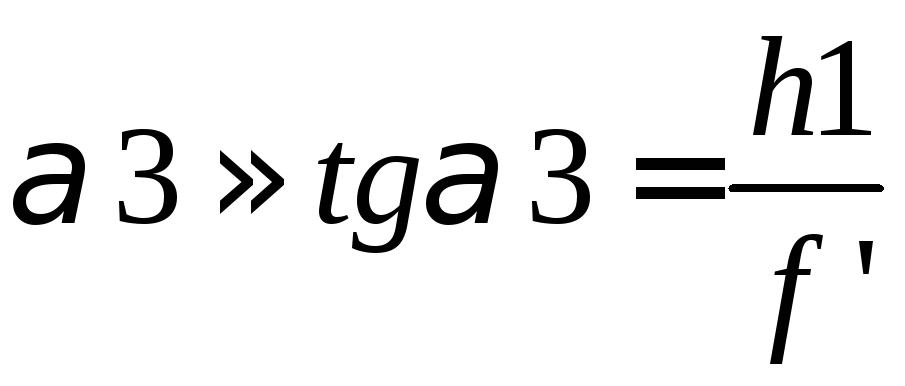. (2.29)

З виразів (2.30) та (2.31) для задньої фокусної відстані f' отримаємо:

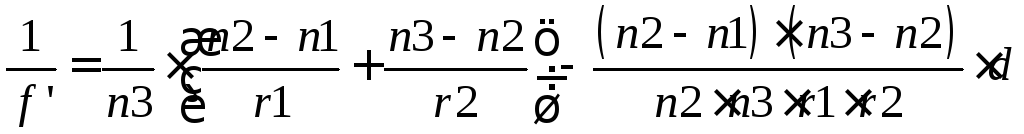. (2.30)

Аналогічно розглядаючи хід променя, паралельного оптичній осі, у зворотному напрямі, для передньої фокусної відстані будемо мати:

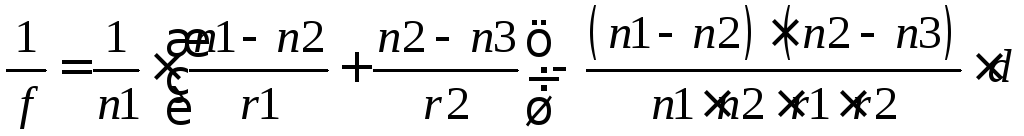(2.31)

Якщо лінза знаходиться у повітрі, то n1 =n3 = 1. Приймаючи показник заломлення матеріалу лінзиn2 = n, вирази для фокусних відстаней набудуть вигляду:

,

,

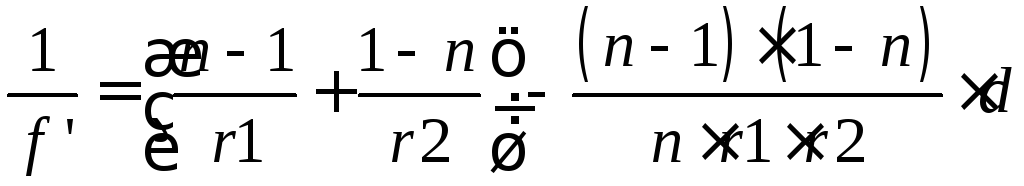або

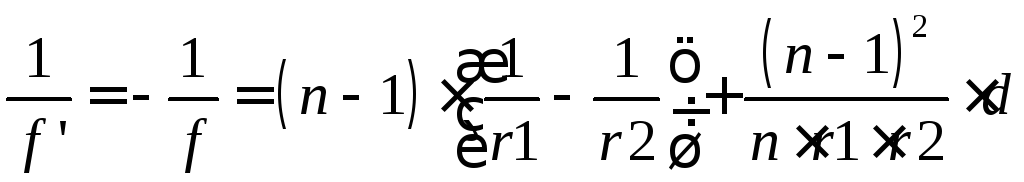. (2.34)

На завершення зазначимо, що у параксіальній області для реальних центрованих оптичних систем справедливі усі формули і положення ідеальної оптичної системи.