3.1.2 Плоский напружений стан

Оскільки при плоскому напруженому стані дві грані елементарного паралелепіпеда вільні від напружень, то для спрощення міркувань сумістимо ці грані з площиною рисунку (рисунок 3.2).

Якщо напруження _x , _y i _xн відомі, то можна визначити напруження на довільній площадці, повернутій на кут відносно площадки, на якій діє напруження(рисунок 3.2)

, (3.2)

, (3.3)

. (3.4)

Із (3.2) і (3.3) випливає, що

,

тобто сума нормальних напружень , що діють на двох взаємно перпендикулярних площадках величина стала.

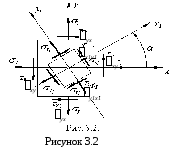Правила знаків. Кут вважається додатним, якщо він відкладається проти руху годинникової стрілки. Розтягувальні нормальні напруження будемо вважати додатними, а стискувальні  від'ємними.

Дотичні напруження вважатимемо додатними 0, коли вони будуть намагатись обертати елемент відносно його центра за годинниковою стрілкою, а від’ємними – проти. Тоді закон парності дотичних напружень набуде вигляду

. (3.5)

3.1.3 Головні площадки і головні напруження

Знайдемо положення головних площадок. На головних площадках дотичні напруження дорівнюють нулю, тому прирівнявши вираз (3.3) до нуля, знайдемо

,

звідки

, (3.6)

або

.

Формула (3.6) дає два значення кута і, які і визначають положення двох головних площадок. Якщо_x  _y i _xн  0 то ₀ буде додатним (рисунок 3.3).

Головні напруження можна визначити за формулами (3.2) і (3.4) якщо замість  підставити ₀ і ₀ + , знайдені за формулою (3.6). Після нескладних перетворень одержимо

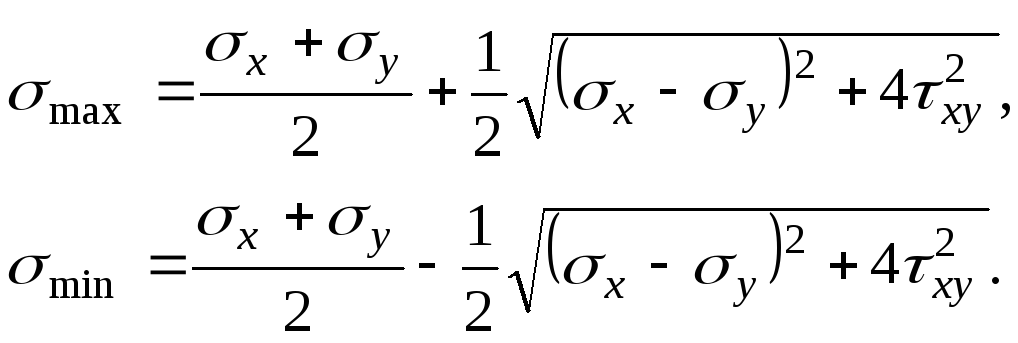(3.7)

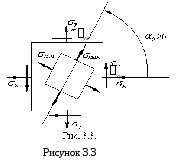
Легко показати, що головні напруження мають екстремальні значення: одне з них є найбільшим з усіх нормальних напружень, які діють на численних площадках, що проходять через дану точку, а друге напруження найменшим.

На площадках, нахилених під кутом 45^ до головних, діють екстремальні дотичні напруження, які рівні

. (3.8)

Нормальні напруження на цих площадках

. (3.9)

3.1.4 Круг напружень

Залежності між складовими напружень та головними напруженнями в даній точці можна виразити графічно за допомогою круга напружень, яке також називається кругом Мора. Теоретичні передумови графічного розв’язування ґрунтуються на залежностях (3.2 – 3.4), які являють собою узагальнені параметричні рівняння кола в системі координат –. Роль параметра відіграє кут, що встановлює відповідність між точкою кола та січною площадкою.

Круг Мора можна побудувати при відомих напруженнях на гранях елемента (рис. 3.4). Нехай D_x– точка, положення якої в системі координат–визначає напруження на площадці, перпендикулярні осі х, тоді D_x(_х;_ху), а D_y(_y;_yх). З врахуванням закону парності дотичних напружень у вигляді (3.5) ці точки лежать на однаковій відстані від осіпо різні сторони. Центр круга Мора завжди лежить на осі, тому, для його побудови, з’єднаємо точки D_x(_х;_ху), а D_y(_y;_yх). Точка перетину відрізку D_xD_yз віссює центром круга Мора. Проводимо коло, що проходить через точки D_x та D_y.

Полюс круга Мора визначає початкове положення елемента = 0. Полюс при прийнятих позначеннях відповідає точці з координатами М(_y;_ху). Проведемо промені з точки М в точки D_x та D_y. Площадки, перпендикулярні цим променям (заштриховані), утворюють початкове положення елемента.

Визначення головних напружень за допомогою круга Мора.

Головні напруження набувають екстремальних значень, тобто одне з них алгебраїчно найбільше, інше – найменше. Напружений стан в точці визначають тільки точки круга Мора, тому найбільше нормальне напруження відповідає крайній правій точці (₁), а найменше – крайній лівій (₂ або₃). Це – діаметрально протилежні точки, що лежать на осі. Положення першої головної площадки визначається кутом, утвореним променем, що проходить через точку (₁) та віссю. Аналогічно визначається положення другої головної площадки, яка завжди повернута на 90⁰відносно першої.

Визначення напружень при повороті площадки за допомогою круга Мора.

Проведемо через полюс М пряму, що утворює кут з віссю. Кутвважається додатним, якщо він відкладається проти руху годинникової стрілки. Ця пряма перетинає круг в деякій точці А. Координати точки А (_х1;_х1у1) визначають напруження на площадці при повороті на кутдо заданої, на якій діють напруження D_x(_х;_ху).

Проведемо через полюс М пряму, що перпендикулярна прямій, яка утворює кут з віссю. Перетин прямої з колом дасть координати точки В (_у1;_у1х1), які визначають напруження на площадці при повороті на кутдо заданої, на якій діють напруження D_у(_у;_ух).