X: 9331 4359 7162 5571 8352;
Y: 7716 6529 2618 6823 9721.
Решение.
8
2
5
3
1
3
9
9
5
3
4
2
6
1
7
1
7
5
5
2
6
7
9
6
7
8
6
5
7
2
2
1
2
1
1
3
8
9
6 Y
а
В
3 X
А
Рис. 11
Превращаем граф в нагруженный, подставляя веса ребер слева направо (по оси Ox) и снизу вверх (по оси Oy) (рис. 11);
б) действуем по
алгоритму: вершине А приписываем индекс
0, остальным вершинам +
.
Вершины, смежные с А, получают новые
индексы: вершина (0; 1): 0 + 9 = 9, вершина
(1; 0): 0 + 7 = 7. Вершина (1; 1) может получить
индекс 7 + 4 = 11 или 9 + 6 = 15.выбираем
наименьший из возможных индексов – 11
(рис 12).
8
2
5
3
3
1
3
9
9
5
3
4
2
6
1
7
1
7
5
5
2
6
7
9
6
7
8
6
5
7
2
2
1
2
1
1
3
8
9
6 Y X
В
А
Рис 12
Действуя аналогичным образом, присваиваем новые индексы всем вершинам. При этом вершина В получает индекс 27 (рис. 13).
8
2
5
3
3
1
3
9
9
5
3
4
2
6
1
7
1
7
5
5
2
6
7
9
6
7
8
6
5
7
2
2
1
2
1
1
3
8
9
6 Y X
В
А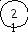
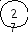
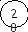
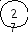
Рис. 13
Индекс 27 = 26 + 1, следовательно, из вершины В нужно идти вниз, в вершину (4; 3) с индексом 26. 26 = 25 + 1, из вершины (4; 3) переходим в вершину (3; 3) с индексом 25. Этот индекс может быть получен двумя способами: 25 = 23 + 2 = 18 + 7, т.е. получаем два пути. 18 = 17 + 1, 23 = 17 + 6; оба пути сходятся в вершине (2; 2). 17 = 16 + 1; 16 = 11 + 5; 11 = 7 + 4; 7 = 0 + 7.
мы вернулись в вершину А. Таким образом, построены два пути с наименьшей суммой весов, равной 27 (рис. 14).
8
2
5
3
3
1
3
9
9
5
3
4
2
6
1
7
1
7
5
5
2
6
7
9
6
7
8
6
5
7
2
2
1
2
1
1
3
8
9
6 Y X
В
А
Рис. 14
Вот эти пути: (0; 0) – (0; 1) - (1; 1) - (1; 2) – (2; 2) – (2; 3) – (3; 3) – (3; 4) – (4; 4)
и (0; 0) – (0; 1) - (1; 1) - (1; 2) – (2; 2) – (3; 2) – (3; 3) – (3; 4) – (4; 4).
Представление графов в памяти компьютера
Пусть дан орграф
с n
пронумерованными вершинами. Матрица
А размером n
n,
заполненная числами
aij=
называется матрицей смежности орграфа.
Такая матрица определяет орграф однозначно вместе с нумерацией вершин.
Точно также строится матрица смежности неориентированного графа. Она обладает дополнительным свойством aij= aji, т.е. матрица симметрична относительно главной диагонали. Поэтому достаточно хранить в памяти только верхний треугольник матрицы смежности A’.
Пусть дан граф с n вершинами. Пронумеруем вершины произвольно и составим матрицу смежности А, поскольку граф не ориентированный, она будет симметрична относительно главной диагонали, поэтому достаточно знать ее верхний треугольник А’ (рис 15).
Рис. 15
Расположим А’ в виде двоичной строки (слева направо, сверху вниз). Меняя нумерацию вершин, мы получим другие двоичные строки. Сравним их между собой как двоичные числа. Наибольшее из двоичных чисел называется кодом Харари, а возникшая при этом нумерация вершин – канонической. Код Харари определяет граф однозначно, но не всякое число может быть кодом Харари.
1. Найти код Харари графа (рис. 16)
Рис. 16