a : x −445 = y −225 = z −−390.

Вариант 30. Построить проекции высоты треугольника АВС, проходящей через вершину С.

А(130, 25, 5), В (90, 75, 75), С (30, 5, 25).

5.8.Контрольные вопросы

5.8.1.Какие задачи называются метрическими? Приведите примеры.

5.8.2.В каком случае плоский угол, отличный от прямого, проецируется на плоскость проекций в натуральную величину?

5.8.3.При каком условии прямой угол проецируется на плоскость проекций в натуральную величину?

5.8.4.Как задается прямая, перпендикулярная плоскости, на комплексном чертеже Монжа?

5.8.5Запишите условие перпендикулярности двух прямых плоскости в аналитическом виде.

5.8.6.Условие перпендикулярности двух плоскостей.

5.8.7.Как определяется кратчайшее расстояние от точки до плоскости, от точки до прямой, между двумя прямыми?

5.8.8.Какие линии называются линиями наибольшего наклона к плоскостям проекций?

6.СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА

6.1.Краткие теоретические сведения

6.1.1. Общие сведения

Решение метрических и позиционных задач значительно упрощается, если хотя бы одна из геометрических фигур, о которых идет речь в задаче, находятся в частном положении относительно плоскостей проекций. Для преобразования геометрических фигур общего положения в фигуры частного положения используются преобразования комплексного чертежа, которые можно разделить на две группы. К первой группе относятся способ замены плоскостей проекций и способ дополнительного проецирования. В этом случае происходит замена исходных плоскостей проекций новыми, относительно которых геометрические фигуры будут находиться в частном положении. Ко второй группе относятся способ плоскопараллельного движения, способ вращения вокруг проецирующей прямой и способ вращения вокруг прямой уровня. При этом изменяется положение геометрических фигур относительно неизменных плоскостей проекций.

Перечисленными способами можно решить следующие четыре основные задачи по преобразованию: 1)прямой общего положения в прямую уровня; 2)прямой общего положения в проецирующую; 3)плоскости общего положения в проецирующую; 4)плоскости общего положения в плоскость

уровня. Задачи 1 и 3 решаются одним преобразованием, а задачи 2 и 4 в общем случае – двумя преобразованиями.

6.1.2.Способ замены плоскостей проекций

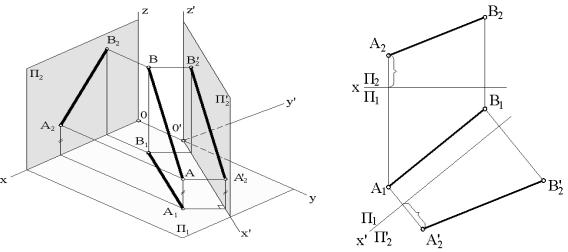
Вданном способе происходит замена одной из исходной плоскостей проекций на новую, по отношению к которой геометрические фигуры будут параллельны или перпендикулярны. На рис. 6.1а, 6.1б показана замена фронтальной плоскости проекций Π2 новой фронтальной плоскостью

проекцийΠ′2 , параллельной отрезку AB .

Пример. На рис.6.2 показано определение натуральной величины плоского треугольника ABC. Задачу решаем c помощью двух

должна быть перпендикулярнаh1 . Во втором преобразовании горизонтальная

плоскость проекций Π1′ параллельна плоскости треугольника ABC. При этом ось O′′x′′ системы плоскостей Π′1,Π′2 будет параллельна проекции A′2B′2C′2

треугольника ABC. На плоскость проекций Π1′ треугольник ABC проецируется в натуральную величину.

Рис.6.1

Рис. 6.2

6.1.3. Способ плоскопараллельного движения

При способе плоскопараллельного движения геометрические фигуры приводятся в частное положение путем их плоскопараллельного перемещения в пространстве относительно неподвижной системы плоскостей проекций. Плоскопараллельным перемещением фигуры относительно некоторой плоскости называется перемещение, при котором все ее точки перемещаются в плоскостях, параллельных этой плоскости. Если фигура совершает плоскопараллельное движение относительно Π1 , то

траектории движения всех ее точек расположены в плоскостях, параллельных Π1 (эти плоскости на Π2 проецируются в прямые,

параллельные оси проекций Ox ) (рис. 6.3а,б). Так как угол наклона к Π1 в

процессе плоскопараллельного перемещения не изменяется, то горизонтальная проекция фигуры остается конгруэнтной самой себе.

Рис. 6.3

Пример. На рис. 6.3б показано определение натуральной величины отрезка AB способом плоскопараллельного движения.

Плоскопараллельным движением относительно плоскости проекций Π1 переводим отрезок AB в положение прямой уровня (фронтали). Его

горизонтальная проекция A1′B1′ станет параллельной оси Ox. Фронтальные проекции A2′,B2′ точек A,B концов отрезка найдем на пересечении линий

связи, проведенных из горизонтальных проекций точек, с фронтальными проекциями Φ2 , 2 горизонтальных плоскостей уровня Φ, , в которых

перемещаются точки A и B.

6.1.4. Способ вращения вокруг проецирующей прямой

Этот способ является частным случаем способа плоскопараллельного движения, когда точки геометрической фигуры перемещаются по дугам окружностей mi (рис.6.4а,б) с центрами, расположенными на оси вращения i.

Рис. 6.4

Пример. Определим натуральную величину отрезка AB.

Будем вращать отрезок AB вокруг горизонтально проецирующей оси i, проходящей через точку А, до тех пор, пока он не будет параллельным фронтальной плоскости проекций Π2 . Точка А останется неподвижной,

поскольку принадлежит оси вращения i. Точка В перемещается по дуге

когда он параллелен Π2 .

6.2.Задачи для аудиторных занятий

6.2.1.Способ замены плоскостей проекций

6.2.1.1.Найти углы наклона прямой a к фронтальной и горизонтальной плоскостям проекций (рис. 6.5)

6.2.1.2.На прямой a общего положения построить проекции отрезка AB длиной 30 мм (рис. 6.5).

6.2.1.3.Построить проекции квадрата ABCD по заданной стороне AB , если известно, что сторона AD принадлежит прямой a (рис. 6.6).

6.2.1.4.Через точку A провести прямую, перпендикулярную прямой m

(рис.6.7).

6.2.1.5.Определить расстояние от точки M до плоскости треугольника

ABC (рис. 6.8).

6.2.1.6.Определить расстояние от точки M до прямой a (рис. 6.9).

6.2.1.7.Определить кратчайшее расстояние между двумя скрещивающимися прямыми a и b (рис. 6.10).

Рис. 6.11

6.2.1.8.Определить величину двугранного угла ABCD (рис. 6.11).

6.2.1.9.Найти точку пересечения медиан треугольника ABC

А(130,15,75), В(100,85,30), С(45,60,105).

6.2.2.Способ плоскопараллельного движения

6.2.2.1.На прямой a от точки A отложить отрезок AB, равный 50 мм

(рис.6.12).

6.2.2.2.Достроить фронтальную проекцию отрезка AB, длина которого

равна 60 мм

A(30,20,40), B(60,50,?).

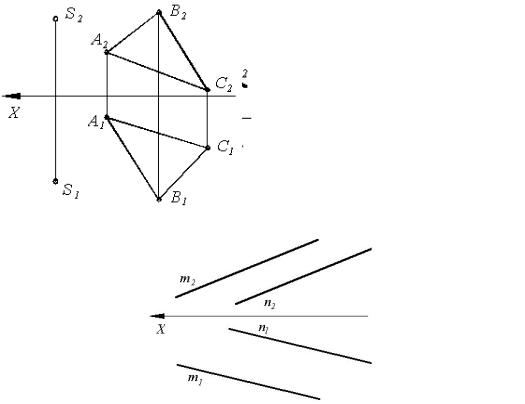
6.2.2.3.Определить радиус сферы с центром в точке S, касающейся заданной плоскости Γ(ABC) (рис. 6.13).

6.2.2.4.Найти центр окружности, вписанной в треугольник ABC.

A(120,60,96), B(48,30,60), C(84,90,30).

Рис. 6.14

6.2.2.5. Найти расстояние между параллельными прямыми m и n (рис.

6.14).

6.2.3.Способ вращения вокруг проецирующей прямой

6.2.3.1.Найти угол наклона прямой a к горизонтальной плоскости проекций Π1 (рис. 6.15).

6.2.3.2.Отрезок AB повернуть вокруг прямой i на угол 60° (рис. 6.16).