lineynaya_algebra_Yudina

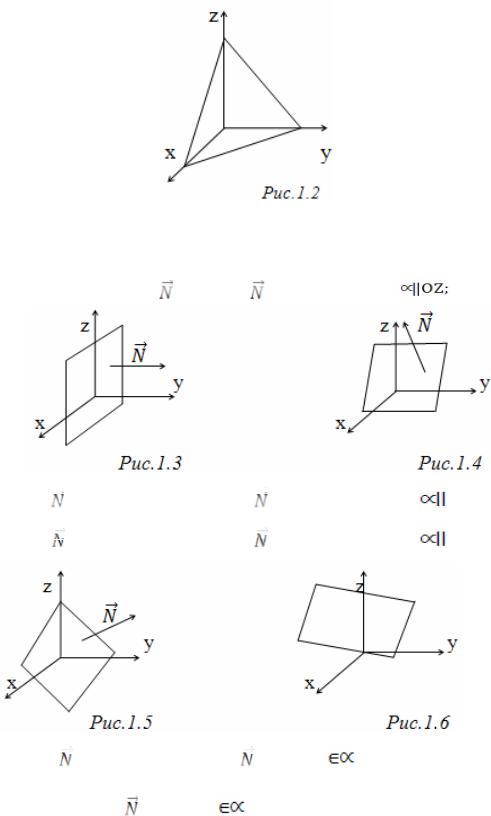
Частные случаи общего уравнения плоскости

ка

Исследуем общее уравнение плоскости Аx+By+Cz+D=0 в зависимости от

коэффициентов.

е

I. Если А,В,С≠0, то плоскость называется общего положения (см.рис.1.2)

и

о

т

б

II. 1) Если D=0, Аx+By+Cz=0; x=y=z=0 – т.е. точка О(0;0;0) начало координат

и

начало координат;

принадлежит плоскости, т.е. плоскость проходит черезл

б

(см.рис.1.3)

2) Если С=0, Аx+By+D=0; =(A,B,0); ┴OZ; плоскость

н

н

ая

┴OY, а плоскость

OY (см.рис.1.4)

3) Если B=0, =(A,0,C); Аx+Cz+D=0;

о

┴OX, а плоскость

OX (см.рис.1.5)

4) Если А=0, =(0,B,C); Аx+Cz+D=0;

е

к

т

р

л

┴OZ; OZ . Плоскость проходит через

III. 1) C=D=0; =(A,B,0); Аx+By=0;

Э

81

ось OZ, (см.рис.1.6)

2) D=B=0; Ax+Cz=0; ┴OY; OY

(см.рис.1.7). Плоскость проходит через

ось OY.

о

е

ка

3) A=D=0; =(0,B,C); By+Cz=0;

┴OX; OX . Плоскость проходит через ось

OX, (см.рис.1.8)

и

т

IV. A=B=0; =(0,0,C); Cz+D=0;

OZ; OY; z= -

.

л

V. 1) D=A=B=0; Cz=0; z=0. Плоскость XOY;

2) A≠0; Ax=0; x=0 – плоскость YOZ;

3) B≠0; By=0; y=0 – плоскость XOZ.

и

б

Уравнение плоскости в отрезках

б

Пусть a,b,c – отрезки, отсекаемые плоскостью на осях. Точки М1(а,0,0),

М2(0,b,0), М3(0,0,с) – принадлежат плоскости α (см.рис.1.9)

Аx+By+Cz+D=0

ая

о

н

н

р

т чек М1, М2, М3 в общее уравнение плоскости.

Подставим коэффициенты

к

т

е

<=>

л

y z=0, D≠0, если плоскость не проходит

Уравн ние плоскости будет x

через нача о координат, поделив на ( –D), получим

Э

82

(1.4) - уравнение плоскости в отрезках

Возьмём произвольную точку М(x,y,z) на плоскости и составим три

вектора ,

и

(см.рис.1.10). =(x-x1;y-y1;z-z1),

=(x2-

x1;y2-y1;z2-z1), =(x3-x1;y3-y1;z3-z1).

т

е

ка

о

и

Уравнение (1.5) есть уравнение плоскости, проходящей через три точки.

и

б

л

Нормальное уравнение плоскости

б

Положение плоскости α в пространстве вполне определяется заданием

нормального

вектора

. Пусть

р сстояние от начала координат равно p

(см.рис.1.11)

Пусть нормальный вектор образует с осями координат углы α, β, γ, тогда

ая

вектор имеет координаты (cosα, cosβ. cosγ). При любом положении точки М

на плоскости

проекция вектора

на направлении равно р.

=р, то есть

* =р.

о

н

н

р

т

к

е

л

Э

83

* -р=0 (1.6) – нормальное уравнение плоскости в векторной форме

Зная коэффициенты векторов

ка

и уравнение (1.6) перепишем в

координатной форме:

xcosα+ycosβ +zcosγ-p=0 (1.7)

е

Уравнение (1.7) называется нормальным уравнением плос ости в

координатной форме.

т

§5.2. Основные задачи на плоскость

о

и

двумя плоскостями, условия параллельности и перпенд кулярности плоскостей

и нахождение расстояния от точки до плоскости.

б

л

ельности и

Угол между двумя плоскостями. Условия пара

перпендикулярности плоскостей

и

Пусть заданы две плоскости α и β уравнен ями:

б

α: A1x+B1y+C1z+D1=0

β: A2x+B2y+C2z+D2=0

Под углом между плоскостями α и β подразумевается один из меньших

ая

к этим

углов, образованных этими плоскостями или нормалями 1 и 2

плоскостям. Поэтому cosφ=

(2.1) или cosφ=

(2.2)

Если

плоскости

α и

β перпендикулярны, то

нормали

1 и

2

тоже

н

=0 (2.3) или

перпендикулярны, следователь о,

о

=0

(2.4).

Условия (2.3)

и (2.4)

есть

условия

перпендикулярности

плоскостейн

. Если плоскости α и β параллельны, то

параллельны будут и н рмали 1 и

2. Условия коллинеарности векторов

1 и

2:

р

(2.5) – это и есть условие параллельности двух плоскостей.

к

т

Расстояние от точки до плоскости

Расстояние d от точки М0(x0,y0,z0) до плоскости вычисляется по формуле

Э

л

d=

(2.6)

84

Вывод этойе

формулы аналогичен выводу формулы расстояния от точки до

плоскости.

Решение:

запишем

каноническое

уравнение

плоскости

А(

)+В(

)+С(

)=0, где координаты (x0,y0,z0) – координаты точ и М0,

а A, B, C – координаты вектора .

т

е

ка

3(х+2)+0(у-3)+4(z-5)=0

о

3x+6+4z-20=0 или 3x+4z-14=0

Расстояние d=

=

= 3,4.

и

§5.3. Уравнения прямой в пространстве

и

б

Векторное уравнение прямойл

б

Положение прямой в пространстве вполне определено, если задана какая-

либо

точка М0(x0,y0,z0)

на прямой и

вектор

=(m,n,p),

параллельный этой

прямой.

ая

о

н

н

р

Вектор

к

называется направляющим вектором. На прямой l пусть задана

точка М0(x0,y0,z0) и =(m,n,p) – направляющий вектор.

Возьмём натпрямой l произвольную точку М(x,y,z). Обозначим радиус-

векторы точ к М0 и М соответственно и .

л

= -

=>

+

(3.1). Вектор

коллинеарен

Э

В ктор

85

вектору

е, поэтому =t, где t R. = t*

Уравнение (3.1) можно переписать в виде

(3.2). Полученное

уравнение называется векторным уравнением прямой.

Канонические уравнения прямой

Перепишем уравнение (3.2) в виде = t, и подставим координаты точки

М0(x0,y0,z0) и вектора =(m,n,p), получим уравнение

=

=

= t (3.3).

т

Уравнения (3.3) называются каноническими уравнениями прямойка в

пространстве.

о

о форма

Замечание. Если одна или две координаты вектора равны нулюе,

записи сохранится.

и

Пусть m=0,

=

=

, это значит, что числитель х-х0=0, то есть

х=х0, вектор

перпендикулярен оси ох.

б

л

б

и

Параметрические уравнен я прямой

ая

Из уравнения

=

=

= t найдём

(3.4)

Уравнения (3.4) называются п р метрическими уравнениями прямой.

н

Уравнения прямой, проходящей через две точки

Пусть прямая l проходит через две точки М1(х1,у1,z1)

и М2(х2,у2,z2). В

н

можно принять вектор , = =(х2-

качестве направляющего вектора

x1; у2-y1; z2-z1).

о

Поскольку прямая l проходит через М1, то в уравнение (3.3) подставим

=

р

=

(3.5).

Уравнения (3.5) называются уравнениями

прямой, проходящей че ез две точки.

к

т

Общие уравнения прямой

Прямую в пространстве можно задать как пересечение двух плоскостей.

Рассмотрим систему уравнений.

л

(3.6)

Э

Каждоее

86

уравнение системы определяет плоскость. Если плоскости не

пара е ьны,

то

уравнения

(3.6)

называют общими

уравнениями прямой в

нулю. Пусть, например,

z=0, тогда система уравнений

имеет единственное

ка

решение. За направляющий вектор прямой можно принять вектор = N1 × N2 .

Пример 3.1.

Написать канонические и параметрические уравнения прямой, заданной

системой уравнений.

т

е

Решение. 1) Найдём точку М0. Пусть z=0,

о

Решив эту систему найдём точку М0(-1;1;0).

2) Найдём направляющий вектор . =(1;2;3), (1;-1;-1).

= N1 × N2 =

=(1;4;-3)

л

=и

3) Канонические уравнения прямой будут:

б

;

=

4) Параметрические уравнения будут:

б

Основные задачи на прямуюи

в пространстве

ая

Основными задачами на прямую в пространстве являются:

прямыми. Угол между прямыми можно найти как угол между направляющими

н

векторами cosφ =

(3.7) или cosφ =

(3.8)

р

о

н

к

е

2) Условия параллельностит

и перпендикулярности прямых в пространстве:

- если прямые l1и l2 параллельны, то = λ или =

= = λ (3.9)

л

взаимно перпендикулярны, то

=0 или

- ес и прямые l1и l2

Э

(3.10)

87

Основными задачами на прямую и плоскость в пространстве являются:

ка

1) Нахождение угла между прямой и плоскостью;

2) Условия параллельности и перпендикулярности прямой и плоскости.

1)Угол между прямой и плоскостью.

е

Пусть

прямая

l

задана

уравнениями

=

=

и плоскость

α:Ах+Ву+Сz+D=0.

о

т

Углом между прямой и плоскостью называется меньший из двух смежных

углов между прямой и её проекцией на плоскость.

и

б

л

и

cos(

)= , а cos(

)=sinφ, тогда sinφ=

(4.1)

ая

б

sinφ =

(4.2)

2) Условия параллельности и перпендикулярности прямой и плоскости в

простр нстве

Если

прямая

l

параллель а плоскости α,

то

и

условие

параллельности прямой и плоскости будет:

=0 или Am+Bn+Cp=0 (4.3)

о

N

Если прямая l перпе дикулярнан

плоскости α, то Ý , отсюда

= λ или

S

н

=

=

= λ (4.4)

Уравнение (4.4) есть условие перпендикулярности прямой и плоскости.

е

к

т

р

§5.5. Цилиндрические поверхности

определяемые

уравнениями

второй

степени

Рассмотрим линии,

л

относительно текущих координат: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0 (5.1)

Э

Коэффициенты уравнения - действительные числа, где А2+В2+С2≠0. Такие

называются

88

второго

порядка.

Ниже будет

инии

линиями (кривыми)

– его образующей (см.рис.5.1).

Будем рассматривать цилиндрические поверхности, направляющие

которых лежат

в одной из

координатных

плоскостей, а образующие

параллельны координатной оси, перпендикулярной этой плоскости.

ка

Пусть в плоскости Оху лежит некоторая линия К, уравнение которой

F(x;y)=0 (5.1)

е

Построим цилиндр с образующими параллельными оси Оz, и направляющейт

К.

Теорема 1. Уравнение цилиндра, образующие котор го параллельны оси

Oz, имеет вид F(x;y)=0, т.е. не содержит координаты z.

л

и

о

б

F(x;y)=0 есть уравнение цилиндра с образующими, параллельными оси Оу,

а F(у;z)=0 – с

образующими,

и

оси Ох. Название цилиндра

параллельными

определяется названием направляющей. Если направляющей служит эллипс

+

б

=1 в плоскости Оху, то соответствующая цилиндрическая поверхность

называется эллиптическим цилиндром (см.рис.5.2)

о

н

н

ая

т

р

к

е

л

Э

89

т

е

ка

и

Частным случаем эллиптического цилиндра является круговой цилиндр, его

уравнение

+ =R2. Уравнение

=2pz определяет

ов

пространстве

параболический цилиндр (см. рис.5.3).

б

-

Уравнение

=1

определяет в

пространстве

гиперболический цилиндр

(см.рис.5.4). Все

эти

поверхности

и

есть уравнения

называются цилиндрами второго порядка, так как их уравнениял

второй степени относительно текущих коорд нат x, y и z.

б

§5.6. Поверхности вращения

ая

некоторая кривая L лежит в плоскости Oyz. Поверхности вращения задаются

н

уравнениями второго порядка.

По заданному урав е ию второго порядка определим его геометрический

н

поверхности будем производить при помощи изучения линий пересечения

о

данной поверхности с коорди атными плоскостями им параллельными.

р

Эллипсоид

Исследуем пове хность, заданную уравнением

+ + =1 (6.1).

к