Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Альметьевский государственный нефтяной институт

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

lineynaya_algebra_Yudina

.pdf

Скачиваний:

Добавлен:

15.05.2015

Размер:

16.87 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

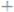
. В качестве характеристики формы эллипса чаще пользуются

отношением

Отношение

половины расстояния между фокусами к большой полуоси

эллипса

эксцентриситетом

эллипса

называется

обознача тся

буквой

(«эпсилон»):

ка

(4.6)

причем 0 < < 1, так как 0 < c < а.

С учетом равенства (4.6) ф рмулу (4.6)

можно переписать в виде

т.е.

Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет

менее сплющенным;

если

положить

эллипс превращается в

= 0, то

окружность.

(4.4)

ая

Рис. 4.5

(см. рис.

Пусть М(х;у) произвольная точка эллипса с фокусами F1 и F2

4.5). Длины отрезк в

называютсян

фокальными радиусами точки M Очевидно,

F1 M=r1 и F2М=r2

= 2а. Имеют место формулы

называются

директрисами

эллипса.

Значение

Прямые

директрисы

эллипса

выявляется

следующим

утверждениемт.

Т ор ма 4.1. Если r — расстояние от произвольной

точки эллипса до какого-нибудь фокуса. d - расстояние

от этой же точки до соответствующей этому фокусу

директрисы, то отношение

есть постоянная величина,

равная эксцентриситету эллипса:

Из равенства (4.7) следует, что а > Ь. Если же а < b.

То уравнение (4.5) определяет эллипс, большая ось которого 2b лежит на оси Оу, а малая ось 2а — на оси Ох (см. рис. 4.6). Фокусы такого эллипса

находятся в точках F1 (0; с) и F2(0; -с), где .

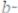
Гипербола

ка

Каноническое уравнение гиперболы

Гиперболой называется множество всех

точек

модуль

плоскос и, е

разности расстояний от каждой из которых до двух данных т чек этой

плоскости, называемых фокусами, есть величина пост янная, меньшая, чем

расстояние между фокусами.

Обозначим фокусы через F1 F2. расстояние

между ними через 2с, а модуль разности расстоян й от каждой точки

гиперболы до фокусов через 2а. По определению 2

2с. т. е. a < с.

Для вывода уравнения гиперболы выберем систему координат Оху так,

чтобы фокусы F1

и F2

лежали на оси Ох,

а начало координат совпало с

удут иметь координаты

серединой отрезка F1 F2 (см. рис. 4.7). Тогда фокусы

F1(-с;0) и F2(с;0). Пусть М(х;у) - произвольная точка гиперболы.

ая

Рис. 4.7

Тогда

согласно

гиперболы

определению

или

т.е.

После

упрощений, как

это

было

сделано

при

выводе

уравнения

эллипса,

получим каноническое урав е ие гиперболы

(4.7)

где

(4.8)

Гипербола есть линия второго порядка.

Исследование формы гиперболы по ее уравнению

Установим форму гиперболы, пользуясь ее каноническим уравнением.

(4.7)

содержит

х и у

только

четных

степенях.

1).Уравнение

Сл довательно, гипербола симметрична относительно осей Ох и Оу, а также
	л
относительно точки О(0; 0), которую называют центром гиперболы.
Э	2).Найдем точки пересечения гиперболы с осями координат. Положив у =0
		72	гиперболы с осью Ох:
в	уравнении (4.7), находим две точки пересечения
		. Положив х = 0 в (4.7), получаем	, чего быть не

может. Следовательно, гипербола ось Оу не пересекает.

Точки

называются вершинами гиперболы, а отрезок

— действительной осью, отрезок

ка

действительной

полуосью гиперболы.

)

Отрезок

соединяющий точки

называется мнимой осью, число b — мнимой полуосью. Прямоугольник со

сторонами 2а и 2b называется основным прямоугольником гиперболы.

Рис.4.8

3).Из уравнения (4.7) следует, что уменьшаемоеи

не меньше единицы,

ая

т.е. что

или

. Это означаетб, что точки гиперболы расположены

справа от прямой

(правая ветвь гиперболы) и слева от прямой

(левая ветвь

гиперболы)

4). Из

уравнения

(4.7) гиперболы видно, что когда

возрастает, то и

возрастает.

того,

что разность

сохраняет

Это следует из

постоянное значение, рав ое единице.

Из сказанного следует,

что

гипербола имеет форму,

изображенную на

рисунке 4.8 (кривая, с ст ящая из двух неограниченных ветвей).

Прямая

называется

асимптотой

неограниченной

кривой К, если

расстояние d от точки M до этой кривой К до этой прямой стремится к нулю

при неограниченном удалении точки M вдоль кривой К от начала координат.

Гипербола

имеет две ассимтоты:

(4.9)

При построениие

гиперболы (4.9) целесообразно сначала построить основной

прямоуго ьник гиперболы (см. рис. 4.9), провести прямые, проходящие через

противоположные вершины этого прямоугольника, — асимптоты гиперболы и

отметить вершины

гиперболы.

Уравнение равносторонней гиперболы, асимптотами которой служат оси
		ка
координат Гипербола (4.9) называется равносторонней, если ее полуоси равны
(а=b). Ее каноническое уравнение
х2-у2 = а2	(4.10)

										е
	Асимптоты равносторонней гиперболы
	имеют уравнения у = х и у = - x и,
									т
	следовательно, являются бисс ктрисами
	координатных углов.						и	о
	координатных углов.
	Рис. 4.9				б	л
					б
Уравнение равносторонней гиперболы, для которой оси Ох и Оу являются
асимптотами, будет иметь вид		.		и
асимптотами, будет иметь вид		.
Эксцентриситетом гиперболы		(4.7) называется отношение расстояния
			б
между фокусами к величине действительной оси г перболы, обозначается :
	ая
	ая
Так как для гиперболы с > а, то эксцентриситет гиперболы больше единицы:
> 1. Эксцентриситет характеризует форму гиперболы.
Прямые	называются директрисами гиперболы. Так как для гиперболы

> 1, то < а. Это значит, что правая директриса расположена между центром и правой вершиной гиперболы, левая — между центром и левой вершиной.

Директрисы гиперболы имеютн

то же свойство

что и директрисы

х2

эллипса. Кривая, пределяемаян

уравнением

−

= 1, также есть гипербола,

действительная ось 2b которой расположена на оси Оу, а мнимая ось 2а — на

оси Ох. Очевидно, ч о гиперболы

имеют общие

асимптоты. Такие гиперболы называются сопряженными.

Парабола

Каноническое уравнение параболы

каждая из которых

Парабо ой называется множество всех точек плоскости,

одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса Р до директрисы называется параметром параболы и обозначается через р (р > 0).

Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F , а начато координа

			у				е	ка
	N		M(x;y)			т
					о
			0	х
	μ		x æ p	х
-				ö
				ö
	2		Fç	;0÷
			Fç	;0÷
		è 2		ø
		è 2		ø
			Рис. 4.10.

расположим посередине между фокусом и директрисой (см.рис. 4.10). В

выбранной системе фокус F имеет

координаты

а уравнение

директрисы имеет вид

, или

Пусть М(х:у) — произвольная точка параболы. Соединим точку M с F.

Проведем отрезок MN перпендикулярно директрисе. Согласно определению

параболы MF=MN. По формуле расстояния между двумя точками находим:

ая

Следовательно,

Возведя обе части урав е ия в квадрат, получим

(4.11)

Уравнение

(4.11)

называется каноническим уравнением параболы. Пара-

бола есть линия в о ого порядка.

Исследование формы параболы по ее

уравнению

1. В уравнении (4.11) переменная у входит в

четной степени, значит, парабола симметрична

относительнол

оси Ох;

ось Ох является осью сим-

метрии параболы.

2. Так как р > 0, то из (4.11)				следует, что x 0. Следовательно, парабола
расположена справа от оси Оу.								ка
расположена справа от оси Оу.
3.	При х=0 имеем у=0.		Следовательно, парабола проходит через н чато
координат.
4.	При неограниченном возрастании х модуль у также неограниченно
5.	возрастает.	Парабола		имеет	вид (форму),		е
изображенный на		рисунке	61.	Точка О(0;	0) называется	т

вершиной параболы, отрезок FM=r называется фокальным радиусом точки M.

является прямоугольная система координат. Другой практически важной системой координат является полярная система координат. Она задается

Уравнения

акже определяют

параболы, они изображены (на рисунке 4.12.)

0 x

Рис. 4.12

Рис. 4.13

ая

Рис. 4.14

, где

Можно показать, что график квадратного трехчлена

любые действительные числа, представляет собой параболу со

смещенной вершиной.

§4.5 Полярная система координат

Подесистемой координат на плоскости понимают способ, позволяющий

чис енно описать положение точки на плоскости. Одной из таких систем

точкой О, называемой полюсом, лучом Оρ , называемым полярной осью и
единичным вектором e	на оси	Оρ .	ка

Положение точки M задается двумя числами: ее расстоянием r от полюса О и углом ϕ , образованным поворотом оси Оρ до совмещения с точкой M

(рис. 5.1). Числа r и ϕ называются полярными координатами точки M, пишут

M(r ;ϕ ), r - это полярный радиус, ϕ - полярный угол, где

−π < ϕ ≤ π (или

0 < ϕ ≤ 2π ), а

0 ≤ r < ∞. В этом случае каждой точке плоскос и (кроме О)

соответствует единственная пара чисел r и ϕ , и обратно.

N ρ

Рис. 5.2

Р с. 5.2

Установим связь между прямоугольными и полярными координатами.

б Совместим полюс О с началом прямоугольнойая системы координат, а полярную

ось – с положительной полуосью Ох (Рис.5.2). Пусть x и y – прямоугольные

координаты точки M, а r и ϕ – ее пол рные.

На рис. 5.1 видно, что

ìx = r cosϕ;

y = r sinϕ.

Полярные координаты точки M выражаются
о	н	н
		ìr =
		ìr =	x2 + y2			;
		ï
		í		y
		ïtgϕ =		y	.
		ïtgϕ =			.
		î		x

Определяя величинуϕ , нужно установить четверть, в которой лежит искомый

угол, и учи ыва ь,рч о −π < ϕ ≤ π .

Пример 5.1.

Дана точка

A(-2;2

3) . Найти полярные координаты точки A.

2 3

Решение. Находим

r = x2 + y2 = 4 +12 = 4 ; tgϕ = −

= − 3 . Т.к. точка А находится

2π

во второй четверти то ϕ = 3 .

ϕ =

2π

, т.е.

A(4;

2π

)

Итак, полярные координаты точки А: r=4,

Пример 5.2.

ка

Дана точка B(

2;− π4 ) . Найти ее прямоугольные координаты.

Решение. Находим x и y

по формулам

π ) =

ïx = r cosϕ =

2 cos(-

= 1;

ïy = r sinϕ =

2 sin(-

) =

2(-

) = -1.

Итак, прямоугольные координаты точки B есть x=1, y=-1, т.е. B(1;1).

Пример 5.3.

(x −1)

+ y

Уравнение окружности

= 1 записать в полярных коорд натах.

Решение. Преобразуем уравнение окружности (x −1)2 + y2 = 1; x2

− 2x +1+ y2 = 1

или

ìx = r cosϕ;

− 2x = 0 . Подставим в уравнение вместо x и y формулыл

+ y

ϕ.

îy = r sin

Получим r 2 cos2 ϕ + r2 sin2 ϕ − 2r cosϕ = 0 ; или r 2 − 2r cosϕ = 0

; r = 2cosϕ .

r = 2cosϕ .

Уравнение окружности в полярных коорд натах будет

§4.6 Задачи для самостоятельной работы

4.1. Составить уравнение прямой,аяпроходящей через точку А(1;1): а) под углом 450 к оси ох; б) параллельноноси оу; в) параллельно прямой 2х-3у+5=0; г) перпендикулярно прямой х-2у+3=0.

4.2. Составить уравнение прямой, проходящей через точки А(-5;4) и В(-3;2). Записать уравнение этой прямой в отрезках и построить её.

4.3. Составить уравне ия двух прямых, проходящих через точку А(-2;3), одна из которых параллель а прямой 3х-2у+1=0, а другая перпендикулярна той же

прямой.							н
4.4. Дан треугольник с вершинами А(-3;1), В(2;7), С(6;-1). Составить уравнения
сторон треугольника, овычислить его внутренние углы. Написать уравнения
высоты и медианы, п оведённых из вершины В.
4.5.		При каких значениях α следующие пары прямых: а) параллельны; б)
						р
перпенди улярны?
1)					т
1)	αх-4у+1=0 и -2х+у+2=0;
2)	4х+у-6=0 и 3х+αу-2=0;
3)				к
3)	х-αу+3=0 и 2х-у+3=0.
		л	е
4.6. Найти расстояние между параллельными прямыми 2х+у-6=0 и 2х+у+2=0.
Э							78
4.7. Определить вид и расположение кривой:
1)	х2+у2+4у-2х-9=0;
2)	2		2
2)	х +2у -4х+16у=0;
3)	16х2-64х-9у2-18у+199=0;

4)	4х2-40х+9у2+3у+100=0;
5)	х2+2х+2у-1=0.	ка
4.8. Найти центр и радиус окружности 3х2+3у2-6х+8у=0.		ка
4.8. Найти центр и радиус окружности 3х2+3у2-6х+8у=0.

4.9. Составить уравнение окружности с радиусом 10, проходящей через точки

А(8;2) и В(10;0).						е
4.10. Составить уравнение окружности, проходящей через точки пересечения
окружности х2+у2+4х-4у=0 с прямой х+у=0 и точку А(4;4).
4.11. Определить полуоси, координаты фокусов и эксцентрисит т							эллипса
9х2+4у2-36=0.
4.12. Составить уравнение эллипса, если его большая полуось						равна 12, а
					и
эксцентриситет 0,8. Найти расстояние между фокусами эллипса. т
4.13. Составить уравнение эллипса, зная, что:				л
а) его большая полуось 5 и фокусы находятся в точках F1(-6;0);оF2(10;0);							Фокусы
б) расстояние между	фокусами 24 и меньшая полуось равна					5.	Фокусы
расположены по оси ох;			б
расположены по оси ох;
в) эксцентриситет ε =	и фокусы (+7;0).	и
		и
4.14. Составить уравнение гиперболы, если её фокусы лежат на оси ох и
расстояние между ними 10, а длина действ тельной полуоси равна 4.
	б

4.15. Составить каноническое уравнение г перболы, если:

а) а=5; с=3; б) с=6; ε=1,5;

в) b=6; уравнения асимптот у=+х.

4.16. Дана гипербола 16х2-9у2=144. Найти: 1) полуоси а и b; 2) фокусы; 3)

эксцентриситет; 4) уравнения	симптот; 5) уравнения директрис.
4.17. Составить уравнения	симптот равносторонней гиперболы у=	и
4.17. Составить уравнения	симптот равносторонней гиперболы у=	и
найти координаты её вершин.	ая

4.18. Определить величи у параметра и расположение относительно
координатных осей следующихнпарабол: 1) у2=3х; 2) х2=4у; 3) у2=-2х; 4) х2=-3у.
4.19. Уравнение линии привести к каноническому виду, построить её:
1)	у=2х2+4х+3;				о	н
2)	у=х2-2х+5;			т
3)	х=у2+5у;			т
4)	х=-у2+2у-2.
			к		2
4.20. К параболе ур=4х проведена касательная параллельно прямой 2х-у+5=0.
Найти уравнение					асательной.
		е
4.21. Найти прямоугольные координаты точек A, B, C, D, для которых известны
	л
полярные координаты: A(2; 0), В(1; -							), С(4; - ), D(1;	).
4.22. Найти полярные координаты точек A, B, C, D, для которых известны
Э						79

прямоуго ьные координаты: A(-4; 4), B(0; -2), C(-1; -1), D(2; 2).

4.23. Написать в полярной системе координат уравнения: а)прямой,
	ка
проходящей через точку А(3; 4) и параллельной полярной оси; б)окружности с
центром в точке В(0; 3) и радиусом, равным 3.

4.24. Написать в полярной системе координат уравнения линий: а) x2+y2=2x; б) (x2+y2)2=а2(x2-y2).

4.25. Построить кривые и написать их уравнения в прямоугольной системе координат: а) τ=2sinφ; б) τ=2cos2φ; в) τ=3(1+cosφ); г) τ=2+ cosφ.

Глава V. Аналитическая геометрия в пространс ве

§5.1. Уравнения плоскости в пространстве

Плоскость в пространстве можно задать различными способами. Каждому

из них соответствует определённый вид уравнения.

ая

Это и есть каноническое урав ение плоскости, где (A,B,C) – координаты

нормального вектора, а (x0,y0,z0) – координаты точки М0.

Общее уравнение плоскости

Раскрыв скобки в у авнении (1.1), получим общее уравнение плоскости:

Аx+By+Cz-(Аx0+Вy0+Сz0)=0

Обозначим -(Аx0+Вy0+Сz0) через D.

Атx+By+Cz+D=0 (1.2) – общее уравнение плоскости

1) Уравн ние плоскости – это уравнение первой степени с тремя переменными;

2) Любое уравнение первой степени определяет некоторую плоскость (при этом

=(A,B,C) – нормаль).

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.05.2015154.55 Кб29kursovaya_NALOGI.docx
#
16.11.20181.11 Mб11kursovaya_PAS.docx
#
15.05.2015383.49 Кб17kurs_proekt_statistika.doc
#
15.05.2015306.18 Кб59Lektsia_9.doc
#
15.05.2015534.02 Кб11lesson.doc
#
15.05.201516.87 Mб18lineynaya_algebra_Yudina.pdf
#
15.05.20151.32 Mб30matem2.doc
#
15.05.2015113.66 Кб19MEPP_kur_r_2012.doc
#
15.05.2015169.98 Кб71Metodichka.doc
#
15.05.20151.23 Mб102metodichka_po_razrabotke_tem_dipl_pr_2014g.doc
#
25.08.201935.14 Кб2Ministerstvo_obrazovania_i_nauki_Respubliki_Tat...docx