Глава 12
Шутки и ошибки
12.1.Ученик Коля Васин при помощи метода математической индукции смог доказать, что в любом табуне все лошади одной масти.
Если есть только одна лошадь, то она своей масти, так что база индукции верна. Для индуктивного перехода предположим, что есть n лошадей (с номерами от 1 до n). По индуктивному предположению лошади с номерами от 1 до n−1 одинаковой масти. Аналогично лошади
сномерами от 2 до n также имеют одинаковую масть. Но лошади с номерами от 2 до n − 1 не могут менять свою масть в зависимости от того как они сгруппированы — это лошади, а не хамелеоны. Поэтому все n лошадей должны быть одинаковой масти.
Есть ли ошибка в этом рассуждении, и если есть, то какая? (См. также 1.4.)
12.2.Иногда вычитая дроби можно вычитать их числители и складывать знаменатели. Например:
9 − 25 |
= |
9 |
− |
25 |
; |
8 − 50 |
= |
8 |
− |
50 |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
6 + 10 |
6 |
10 |
2 + 5 |
2 |
5 |
|||||||||||
|
|
|
|
|
|
|||||||||||
Для каких дробей это возможно?
12.3. Найдите все дроби с числителем и знаменателем не превосходящими 100, в которых можно проводить сокращение на равные цифры. Примером может служить равенство
6416 = 14.
12.4. Легко проверить равенства
log 16 + 1615 = log 16 + log 1615; log 647 − 8 = log 647 − log 8.
Вкаких еще случаях можно выносить логарифм за скобку?
12.5.При каких значениях a и b возможно равенство
sin a + sin b = sin(a + b)?
169
12.6.Квадраты двух зеркальных чисел 12 и 21 также являются зеркальными числами (144 и 441). Какие двузначные числа обладают аналогичным свойством? И дополнительный вопрос: в каких системах счисления число 441 будет полным квадратом?
12.7.Черная пятница. Докажите, что тринадцатое число месяца
сбольшей вероятностью приходится на пятницу, чем на другие дни недели. Предполагается, что мы живем по Григорианскому стилю (см. 3.153).
12.8.Коля Васин, решая задачу, получил в ответе шестизначное число. А потом он подумал, что это произведение двух трехзначных чисел и выполнил умножение. Каким был первоначальный ответ, если второй ответ оказался в три раза меньше?
12.9.Восстановите алфавит племени Мумбо-Юмбо из задачи 2.6.
12.10.Найдите коэффициент при x у многочлена
(x − a)(x − b)(x − c) . . . (x − z).
12.11. «1 = −1». Изучив комплексные числа, Коля Васин решил вывести формулу, которая носила бы его имя. После нескольких попыток ему это удалось:
r |
|
|
= r |
|
|
|
|
|
|
|
|
|
|
|
|
|
√1√1 = √−1√−1 1 = −1. |
||||||||||
|
−1 |
1 |
|
|
√−1 = |
√1 |
|
||||||||||||||||||||
|
1 |
|
|
−1 |
|
√1 |
√−1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
После некоторых |
размышлений, Коля придумал более короткое дока- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
зательство своего тождества:
√ √ p √
−1 = i2 = −1 · −1 = (−1)(−1) = 1 = 1.
Не ошибся ли где-нибудь Коля Васин? (См. также 7.24.)
12.12. После экспериментов с мнимой единицей, Коля Васин занялся комплексной экспонентой. Пользуясь формулами задачи 7.51, он смог доказать, что sin x всегда равен нулю, а cos x — единице:
sin x = |
eix − e−ix |
|
= |
(e2πi)x/(2π) − (e−2πi)x/(2π) |
|
= |
1 − 1 |
= 0; |
|||||
|
2i |
|
|
2i |
|
|
|
2i |
|
||||
|
|
|
|
|
|
|
|
||||||
cos x = |
eix + e−ix |
= |
(e2πi)x/(2π) + (e−2πi)x/(2π) |
= |
1 + 1 |
= 1. |
|||||||
|
|
2 |
|
|
2 |
|
|||||||
2 |
|
|
|
|
|
|
|||||||
Где ошибка в приведенных равенствах? (См. также 7.55.)
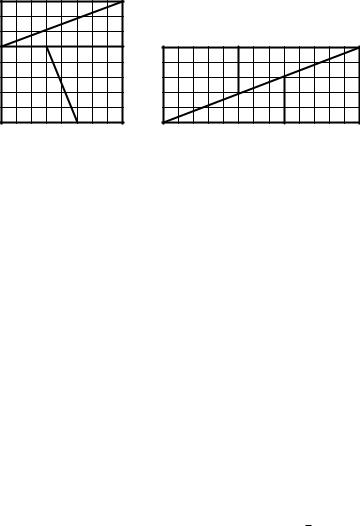
12.13. «65 = 64 = 63». Тождество Кассини лежит в основе одного геометрического парадокса. Он заключается в том, что можно взять
170 |
12. Шутки и ошибки |
шахматную доску, разрезать ее на четыре части, как показано ниже, а затем составить из этих же частей прямоугольник:
Как расположить те же четыре части шахматной доски, чтобы доказать равенство «64 = 63»? (См. также 3.112.)
12.14. Из километров — в мили. В задаче 3.125 была введена фибоначчиева система счисления. Она оказывается удобной, когда нужно сделать перевод расстояния из километров в мили или наоборот.
Предположим, что мы хотим узнать, сколько миль в 30 километрах. Для этого представляем число 30 в фибоначчиевой системе счисления:
30 = 21 + 8 + 1 = F8 + F6 + F2 = (1010001)F.
Теперь нужно сдвинуть каждое число на одну позицию вправо, получая
F7 + F5 + F1 = 13 + 5 + 1 = 19 = (101001)F.
Поэтому предполагаемый результат — 19 миль. (Правильный ответ — около 18,46 миль.) Аналогично делается перевод из миль в километры.
Объясните, почему работает такой алгоритм. Проверьте, что он дает округленное число миль в n километрах при всех n 6 100, отличающееся от правильного ответа меньше чем на 2/3 мили.
12.15. Обозначим через S сумму следующего ряда:
S = 1 − 1 + 1 − 1 + 1 − . . . |
(12.1) |
Преобразовав равенство (12.1), можно получить уравнение, из которого находится S:
S = 1 − (1 − 1 + 1 − 1 + . . . ) = 1 − S S = 12.
Сумму S можно также найти объединяя слагаемые ряда (12.1) в пары:
S = (1 − 1) + (1 − 1) + . . . = 0 + 0 + . . . = 0;
S = 1 − (1 − 1) − (1 − 1) − . . . = 1 − 0 − 0 − . . . = 1.
171
Наконец, переставив местами соседние слагаемые, получаем еще одно значение S:
S = −1 + 1 − 1 + 1 − 1 + . . . = −1 + (1 − 1) + (1 − 1) + . . . = −1.
Итак, действуя четырьмя разными способами, мы нашли четыре значе-
ния суммы S:
S = 12 = 0 = 1 = −1.
Какое же значение имеет сумма S в действительности?