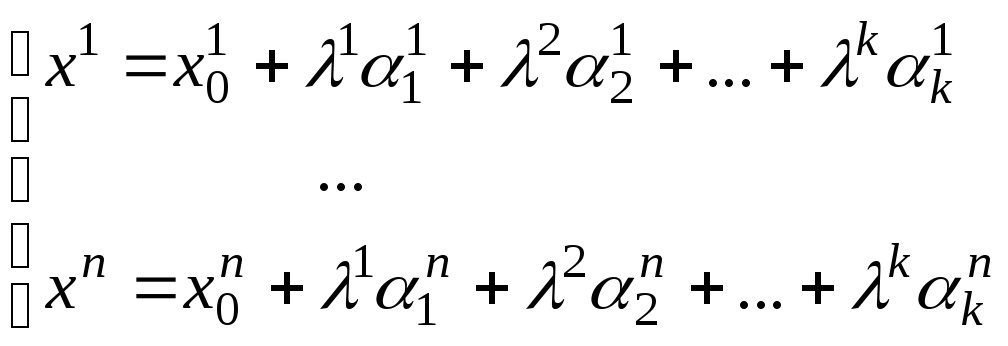§3. Плоскости в аффинном пространстве

1˚. Определения и простейшие свойства.

Пусть в –мерном аффинном пространстве А зафиксирована точка и в соответствующем векторном пространстве взято некоторое произвольное _–мерное подпространство .

Определение 1. Множество всех точек аффинного пространства, для которых , называется –мерной плоскостью, проходящей через точку в направлении подпространства .

Подпространство называют также направляющим подпространством плоскости, точку − текущей точкой плоскости.

Частные случаи.

1) Если , то плоскость –мерная и это просто точка .

2) Если , то эта одномерная плоскость называется прямой линией или просто прямой.

3) Если , то плоскость называется гиперплоскостью.

4) Если , то плоскость совпадает со всем пространством.

Замечание 1. В Определении 1 выделена точка . Покажем, что в качестве можно выбрать любую другую точку плоскости . Пусть точка принадлежит плоскости . Покажем, что эта точка может играть роль точки , т.е. текущая точка . На самом деле, пусть .

Значит, . Обратно, пусть , .

Теорема 1. Всякая –мерная плоскость в аффинном пространстве сама является –мерным аффинным пространством.

Доказательство: Пусть − плоскость, проходящая через точку в направлении подпространства . Возьмем две произвольные точки , и значит, аффинному пространству. По определению аффинного пространства вектор . Также по определению плоскости векторы . Следовательно, . Таким образом, каждой паре точек плоскости соответствует вектор –мерного векторного пространства. Первая аксиома аффинного пространства выполняется для всех точек аффинного пространства, а вторая вытекает из определения –мерной плоскости. ■

Замечание 2. Если плоскость проходит через начало аффинной системы координат в направлении подпространства , то совокупность радиус-векторов ее точек образует линейное пространство, по определению совпадающее с подпространством .

Замечание 3. Пусть в аффинном пространстве А заданы точка . Будем говорить, что эти точки находятся в общем положении, если они не принадлежат одной –мерной плоскости. Очевидно, что точки находятся в общем положении векторы линейно независимы (доказать самостоятельно). Более того, если точки находятся в общем положении, то из определения плоскости следует, что через них проходит –мерная плоскость и при том единственная (доказательство см. Воеводин).

Следовательно, через две точки проходит единственная прямая, через точек – единственная гиперплоскость.

2˚. Векторные и координатные параметрические уравнения плоскости.

Пусть в –мерном аффинном пространстве А зафиксирована аффинная система координат с началом в точке и базисом . Рассмотрим плоскость , проходящую через точку в направлении подпространства .

Пусть , и пусть определяется как линейная оболочка линейно независимых векторов . Тогда радиус–вектор текущей точки плоскости можно записать в виде:

,

т.е.

(1)

− векторное уравнение –мерной плоскости.

Разложим по базису : . Тогда в координатах уравнения (1) перепишутся в виде:

(2)

− координатные параметрические уравнения –мерной плоскости.

Если плоскость проходит через начало координат, то , и, значит, уравнения (2) будут в этом случае параметрическими уравнениями направляющего пространства.

Легко видеть, что справедливо и обратное: множество точек, удовлетворяющих (2), есть –мерная плоскость, проходящая через точку в направлении подпространства , натянутого на векторы .