§9. Линейные преобразования векторных пространств.

1. Основное определение. Ранее рассматривали функции, т.е. ставится в соответствие число. Теперь – обобщение.

Определение 1. Пусть -n-мерному векторному пространству поставлен в соответствие (тому же пространству). Соответствиеназовём преобразованием пространства.

Преобразование называется линейным, если

1. 

2. 

Примеры:

1. Пусть L₂ – подпространство в трехмерном пространстве L₃. соответствующемуL₃ поставим в соответствие его проекцию на L₂ : . Это линейное преобразование, свойства 1, 2 – легко проверяются.

2. Пусть - матрица,L – пространство n – чисел ..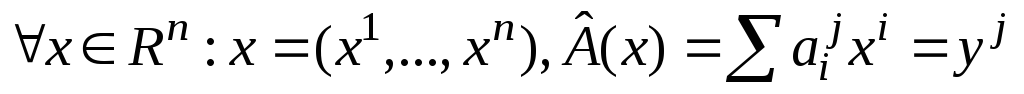 Это линейное преобразование.

3. L_n – пространство многочленов степени . Пусть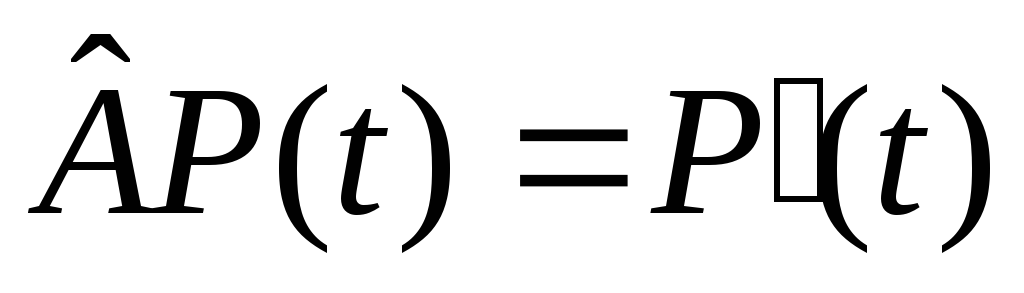- т.е. производная многочлена. Линейность – очевидна.

4. L=C[a,b], - линейностьиз свойств интеграла.

Это пример преобразования в бесконечномерном пространстве. Далее – лишь конечномерные.

2. Матрица линейного преобразования.

Пусть - базис ви- линейное преобразование. Каждый. Векторыне зависят отx и они м. б. разложены по базису:, т.е. если, где

(1)

Определение 2. Матрицей линейного преобразования в базисеназывается матрица (1), столбцы которой – координаты образов векторовв базисе.

Предположение 1. Выбор базиса в устанавливает взаимно однозначное соответствие между линейными преобразованиями этого пространства и квадратными матрицами порядкаn.

Док-во: Итак, показано, что если выбран базис, то любому преобразованию соответствует матрица (1). В соответствии с примером 2 из пункта 1, любой матрице соответствует линейное преобразование. Осталось проверить, что разным матрицам соответствуют разные преобразования. Пусть и- разные преобразования, т.е.. Если они имеют одну и туже матрицуA, то для x имеем: ,то противоречит.

При изменении базиса матрица линейного преобразования вообще говоря изменяется.

Примеры:

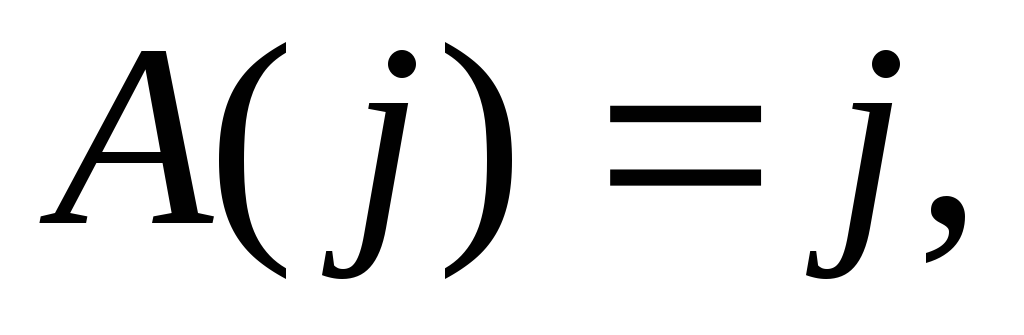
1. Пусть L – трёхмерное пространство с базисом , а- оператор проектирования на плоскость. Тогдаматрица.

2. Если -тождественное преобразование, то

3. L_n –многочлены степени ..

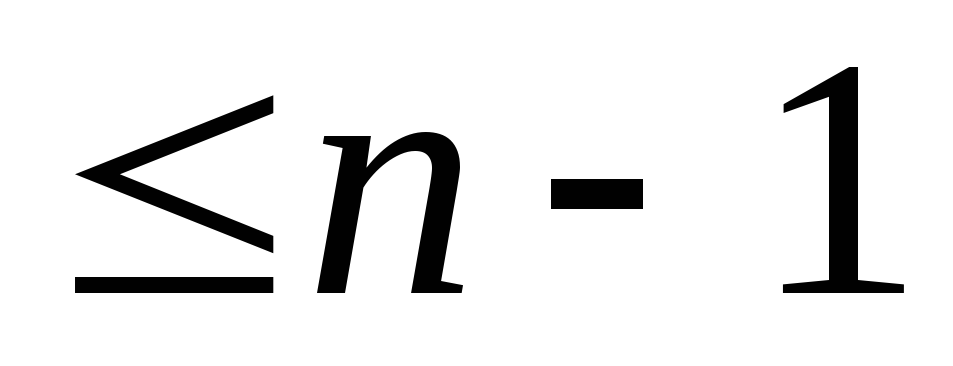Базис L_n : .

Тогда .

Т.о. матрица .

Рассмотрим формулы преобразования A при переходе к другому базису. Пусть . Пусть.

Свойства:

1. Ранг матрицы линейного оператора при переходе от одного базиса к другому является инвариантом.

2. Определитель матрицы линейного оператора инвариантен.

Док-во: Следует из свойств ранга и определителя.

3.Сложение и умножение линейных преобразований.

Определение 3. Произведением линейных преобразований иназывается.

Очевидно, что -линейное преобразование: .

Если - единичное преобразование, то.

Можно определить степени преобразований: .

Тогда .

Пусть в базисе преобразованиюсоответствует матрица,,. ВыразимC через A и B.

По определению

Далее , т.е.есть сумма произведений элементовi-ой строки A на j-ый столбец B C=AB – произведение матриц все свойства произведения матриц переносятся на преобразования (ассоциативность, не коммутативность).

Определение 4. Суммой преобразований иназывается. Легко показать, что матрица С=A+B.

Операции сложения и умножения удовлетворяют обычным свойствам сложения и умножения матриц. Это следует из того, что между матрицами и преобразованиями есть взаимно однозначное соответствие. Нулевое преобразование – нулевая матрица.

Предложение 2. Множество преобразований линейного пространства образует кольцо, называемое кольцом эндоморфизмов.

Определение 5. Произведением линейного преобразования на числоназывается преобразование.

Свойства: очевидны.

Предложение 3. множество линейных преобразований образует линейное пространство размерности .

Следствие. Матрицы – линейно зависимымножеств степени

4.Обратное преобразование. Ядро и образ преобразования.

Определение 6. Преобразование называется обратным к, если, где- единичное преобразование.

Обратное преобразование обозначается .

Обратное преобразование не у всех. Известно, что если у матрицыA , т. и т.т., к.

Предложение 4. Преобразование имеет обратноеего матрица в некотором базисе имеет. Такое преобразование называется невырожденным.

Очевидно, что невырожденные преобразования являются взаимнооднозначными.

Определение 7. Взаимнооднозначное преобразование L_n называется автоморфизмом.

Предложение 5. Множество автоморфизмов линейного пространства образует группу, изоморфную группе невырожденных матриц.

Далее – ядро и образ линейного преобразования.

Определение 8. Совокупность M всех векторов вида , где, называют образом пространстваL_n при преобразовании A.

Предложение 6. M – подпространство в L_n.

Док-во: Пусть

Аналогично, из

Определение 9. Размерность M называется рангом A.

Пример: Ранг преобразования проектирования из V₃ в V₂ имеет ранг 2.

Определение 10. Совокупность N векторов , называется ядром преобразованияA.

Предложение 7. N – подпространство в L_n.

Док-во: Если

Очевидно, что если A не вырожденное преобразование, то его ядро состоит лишь из нуля.

Теорема 1. Пусть A – произвольное линейное преобразование в L_n. Тогда

Док-во: Пусть . Тогда- базис в ядреN, который может быть дополнен до базиса . Рассмотрим. Множество этих векторов образует подпространство, совпадающее с М. Действительно, еслиy - произвольный вектор из M, то , ч.т.д.

Покажем, что вектора - линейно независимы. От противного.

Пусть . Рассмотрим. Тогда, т.е.. Противоречие, т.к. с одной стороныx представим как линейная комбинация базисных векторов ядра, т.е. , с другой стороны. Это противоречит единственности представления вектора в базисе- линейно независимы

5.Инвариантные подпространства линейного оператора.

Определение 11. Пусть - линейное преобразование в. Линейное подпространствоназывается инвариантным относительно, если.

Тривиальные инвариантные подпространства – это нулевое подпространство и всё .

Примеры:

1) ,- вращение относительно некоторой прямой, проходящей через нуль. Инвариантные подпространства – ось вращения и любая плоскость, перпендикулярная оси вращения.

2) ‑ плоскость,.инвариантные подпространства – прямые, проходящие через начало координат.

3) - многочлены степени. Множество многочленов степени,- инвариантное подпространство относительно дифференцирования.

4) Пусть в матрица линейного преобразованияимеет вид

в базисе . Тогда- инвариантное подпространство. Если, то- тоже инвариантное подпространство.

Теорема 2. Сумма и пересечение инвариантных подпространств относительно оператора являются инвариантными подпространствами.

Доказательство. Пусть и- инвариантные подпространстваотносительно, т.е. еслии. Рассмотрим. Пустьеслипересечению, то ипринадлежит пересечению.

Рассмотрим теперь , имеем, гдеи,сумма инвариантных подпространств – инвариантное подпространство.

Выясним, какой вид принимает матрица линейного оператора в , еслии базис всостоит из базисави базисав. Т.к.и- инвариантные подпространства, то.

Получилась квазидиагональная матрица, т.е. состоит из клеток, стоящих на главной диагонали, и- матрицы операторав подпространствахисоответственно. ■