§16. Гиперповерхности второго порядка в вещественном аффинном пространстве.

1. Закон преобразования коэффициентов.

Рассмотрим n – мерное аффинное пространство .

Def 1. Гиперповерхностью второго порядка будем называть геометрическое место точек х, удовлетворяющих уравнению

. (1)

Рассмотрим как изменяются коэффициенты уравнения (1) при переходе к новому базису. Напомним, что декартова система координат аффинного пространства состоит из начала и базиса соответствующего векторного пространства.

Если изменяется базис при неизменном начале:

,

то , после подстановки в (1) ,

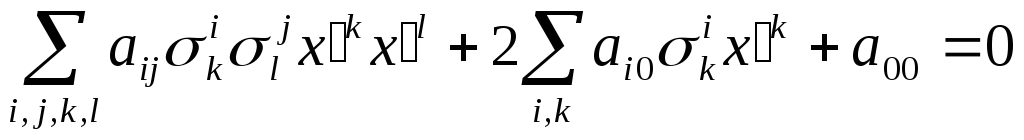т.е.

, , . (2)

Если перенести начало координат в точку с координатами , то

после подстановки в (1)

, . (3)

X.3. Изменение выписать самостоятельно.

Из (2), (3) видно, что при переносе начало координат не меняется, а при изменении базиса изменяются как координаты квадратичной формы, следовательно, многочлен

(4)

можно рассматривать как квадратичную форму, которую будем называть малой квадратичной формой

Предложение 1. Ранг и сигнатура квадратичной формы (4) не изменяются при изменении декартовой системы координат.

Мы получили два инварианта уравнения (1). Для получения еще двух рассмотрим многочлен в пространстве n+1 переменной :

. (5)

1. Получается из (5) при .

При произвольной линейной замене переменных координат (5), преобразованных как элементы матрицы квадратичной формы, которую мы называем большой квадратичной формой.

Мы рассмотрим лишь частный случай, не изменяющий

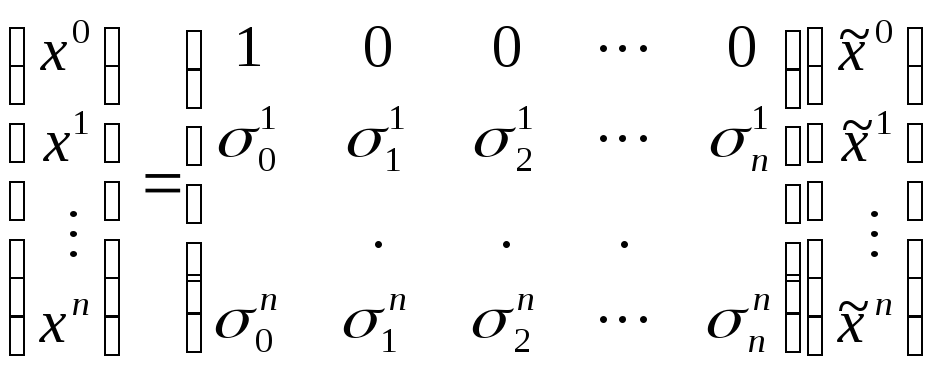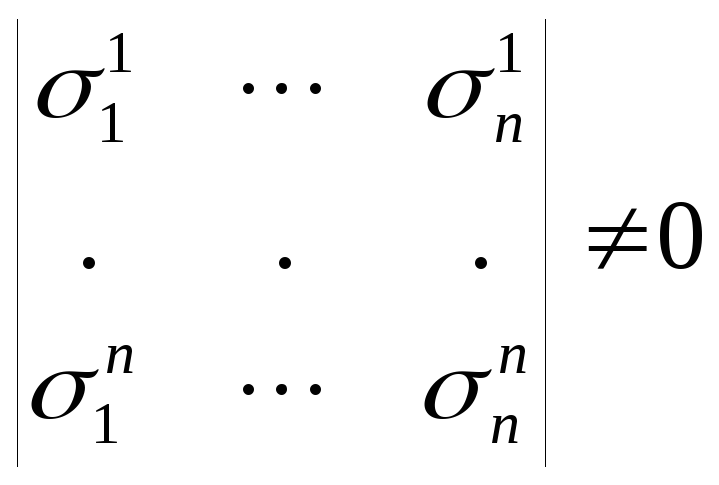, . (6)

.

Если , то получается наиболее общая замена декартовой системы координат в

Предложение 2. Ранг и сигнатура квадратичной формы (5) не изменятся при замене декартовой системы координат.

Если (1) умножить на число , то ранги (1) и (5) не изменятся, а изменятся лишь сигнатуры

Теорема 1. Четыре числа – ранги r и Rи модули сигнатур s и S квадратичных форм (4), (5) являются инвариантами гиперповерхностей второго порядка.

2º. Линии второго порядка на плоскости.

Ранее было показано, что все кривые второго порядка на плоскости за счет выбора базиса могут быть приведены к 9 каноническим видам, следовательно, существует 7 видов линий второго порядка на плоскости (исключая мнимый эллипс и мнимые параллельные прямые). Составляя квадратичные формы (4), (5) для этих кривых, мы вычислим r, R, s, S для всех кривых. Исключение для параболы, где матрица для (5):

.

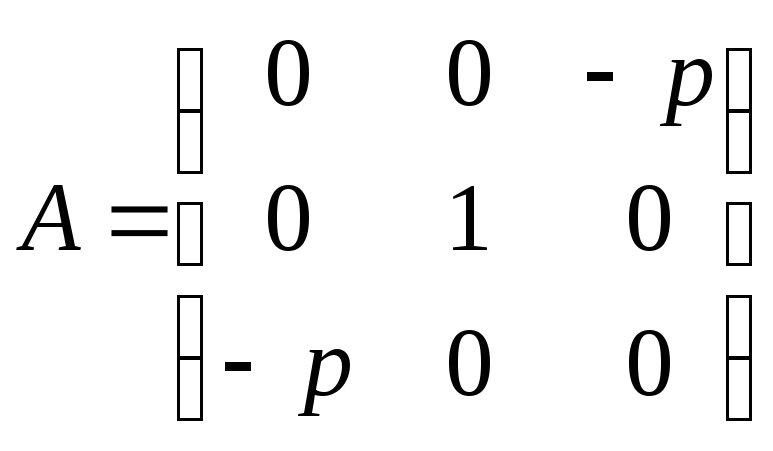Однако после преобразования с

,

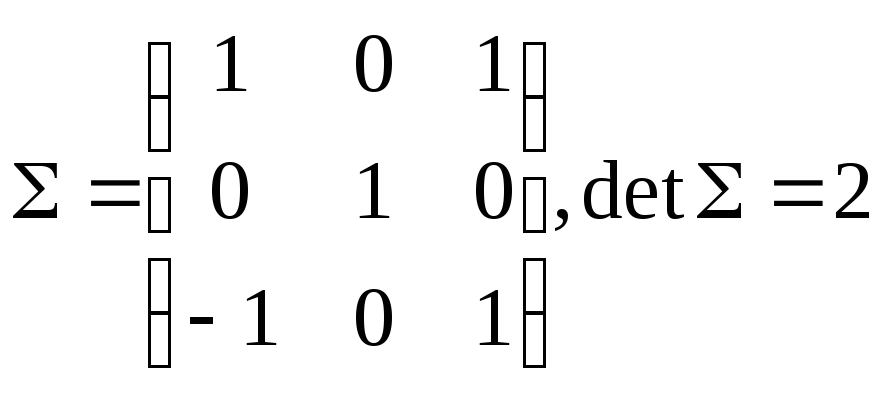получим

,

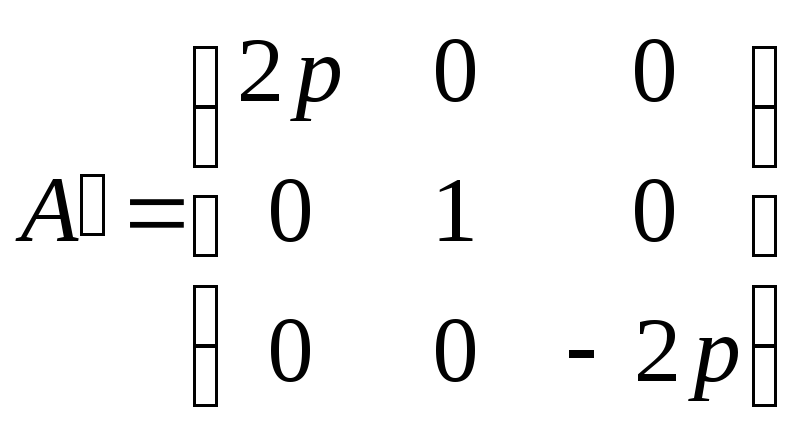т.е. R=3, S=1.

Отметим, что знак сохраняется после преобразований на плоскости, следовательно, >0 – эллиптический тип, <0 – гиперболический, =0 – параболический.

№	название	Каноническое уравнение	R	S	r	s
1 2 3 4 5 6 7 8 9	Эллипс Мнимый эллипс Пара мнимых пересекающихся прямых Гипербола Пара пресекающихся прямых Парабола Пара параллельных прямых Пара мнимых параллельных прямых Две совпадающие прямые		3 3 2 3 2 3 2 2 1	1 3 2 1 0 1 0 2 1	2 2 2 2 2 1 1 1 1	2 2 2 0 0 1 1 1 1