Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Липецкий государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекц

.pdf

Скачиваний:

Добавлен:

11.05.2015

Размер:

2.18 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

МЕТОДИ ПЕРЕТВОРЕННЯ КОМПЛЕКСНИХ КРЕСЛЕНЬ

Розв’язання більшості геометричних

задач зводиться

до визначення метричних

та

позиційних характеристик окремих фігур. Фігура або геометричний елемент по відношенню до

площин проекцій П1, П2 та П3

може займати загальне (незручне)

і окреме (зручне) положення.

При загальному положенні геометричних елементів і фігур розв’язок задач, як правило, більш

складний і триваліший за часом. Але від зміни розташування фігур відносно площин проекцій її

характеристики не міняються. Тобто, після перетворення комплексного креслення додаткові

проекції дають можливість розв’язати задачі найпростішими графічними способами.

Основними методами перетворення креслень є: - заміна площин проекцій;- плоско-

паралельне переміщення (обертання навколо невиявлених осей);- обертання навколо

проекціюючих осей;- обертання навколо ліній рівня.

Заміна площин проекцій.

Суть методу заміни площин проекцій полягає в тому, що

розташування елементів або

фігур залишається незмінним, а змінюється розташування площин проекцій. На рис.І.40

системі площин проекцій П1

та П2

показано

пряму

загального

положення

АВ.

Перпендикулярно до площини П1 введено нову вертикальну площину П4, таким чином, щоб

задана пряма проекціювалясь на неї в натуральну величину, тобто

паралельно до заданого

відрізку АВ. Таким чином, замість системи площин проекцій П1П2 з проекціями відрізка

А1В1, А2В2,

одержано систему П1П4 з

проекціями точок А1В1,

А44В4,

При такій заміні

відстань від старої проекції до старої осі дорівнює відстані від нової проекції до нової осі. На

комплексному кресленні (рис.І.40б) цю відстань показано подвійною рискою.

Нові площини вибираються завжди перпендикулярно до старих і так, щоб фігури

проекціювалися на них в окремомуположенні.

Основні задачі перетворення креслень:

а) визначення натуральної величини

а)

відрізка

прямої.

На

рис.І.41а

(перша

дія)

П2

зображено

відрізок

прямої

загального

положення АВ, перенесеної з рис. І.40б.

В4

В2

Щоб

одержати

натуральну

величину

П4

відрізка АВ,

провели нову вісь х14

паралельно

н.в.

до горизонтальної проекції відрізка в будь-

якому місці. З точок

А1,В1 перпендикулярно

до нової осі

провели лінії зв’язку та відклали

х14

на них від осі х14

координати z точок А і В (з

В1

попередньої, фронтальної проекції). Таким

П1

чином одержали натуральну величину відрізка

х14ІІ А1В1

А4В4.

б)

В2

б) перетворення прямої загального

положення в проекціюючу пряму.

Для цього

треба виконати дві дії: перша – визначення

натуральної величини (описана в пункті а);

друга – перетворення прямої в проекціюючу

х12

В1

пряму.

Виконуємо

другу

дію.

Вводимо

площину, перпендикулярну до натуральної

А1

величини відрізка А4В4 (вісь

х45),

проводимо

А4

н.в.

В4

лінії зв’язку перпендикулярно

до осі

х45.

х14

Рис.І.40

Відклавши відстань, позначену "галочкою",

одержимо

проекцію

прямої

А5В5,

яка

спроекціювалась в точку.
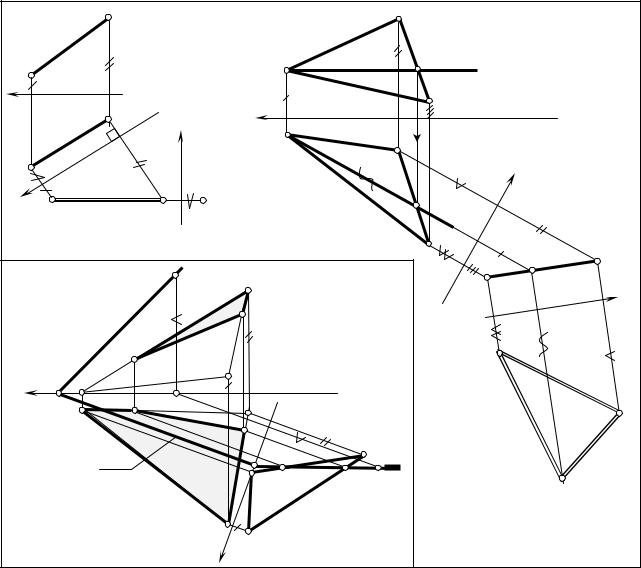
в) перетворення площини загального положення в проекціюючеположення. Для цього
в площині трикутника було проведено горизонталь А-1. Перпендикулярно до горизонтальної
проекції горизонталі (рис.І.41а) вибрано вертикальну площину (її горизонтальний слід - х14).
При цьому горизонталь спроекціювалася у точку А4							≡ 14, а весь відсік - в пряму С4А4В4.
г) перетворення площини загального положення в площину рівня (визначення
натуральної величини відсіку площини).
Для цього треба скористатись проектуючим положенням площини, тобто виконати дії,
описані в пункті в).
Паралельно прямій С4А4В4 (рис. І.41б) проведено слід площини х45									та визначено
натуральну величину трикутного відсіку, причому відстані до вершин трикутника беремо з
площини проекцій П1.
а)			В2				B2		б)
А					A2		12	h2
А
х12
			В1	Х45	X П2			C
				Х45	П1		B1
					П1
					A1
А					A1			X14
А								X14
х14	А4		В4	А5 ≡В5
	А4		В4
							11	h1
							11	h1
							C		B4
									B4
				12	B2			C	A4≡14
								C	X45
					L2				X45
			Σ(f02)		L2
			Σ(f02)
			K2					C
				C2				C
		A2		C2
X	П2	A2
	П2			11
	П1	A1	K1	11	B1
		A1							B5
					L1		B4
							B4
			Σ(h01)				Σ4
					A4 K4	L4	14		A5
									A5
				C1
Рис.І.42.				X14	C4				Рис.І.41.
Рис.І.42.				X14					Рис.І.41.
Приклад 1.Методом заміни площин проекцій побудувати лінію перетину двох площин, одна
з яких задана трикутником АВС, а друга Σзадана слідами (рис.І.42).
Розв’язок. Площину Σ , яка знаходиться в загальному положенні, перетворимо в
проекціюючу площину. Для цього введемо нову площину перпендикулярно до горизонтальної
проекції горизонтального сліду Σ(h01). На П4						позначаємо точки перетинуК і L та переносимо
їх на	проекції		П1 та П2.

II.

Плоскопаралельне переміщення

(обертання навколо невиявлених осей)

Якщо при способі заміни площин проекцій геометричні фігури залишаються на місці, а

до них певним чином підбираються площини проекцій, то при способі плоскопаралельного

переміщення роблять навпаки: площини проекцій П1 та П2

залишаються незмінними, а

геометричні фігури переміщуються так, що кожна точка рухається в площині,

паралельній одній площині проекцій.

На рис.І.43

показано перетворення відрізка АВ прямої в горизонтальну пряму рівня,

потім – в проекціююче положення. Дія перша – відрізок розміщено паралельно площині П1,

при

цьому

кінцеві

точки

відрізка

переміщуються

фронтальних

площинах

а)

(А2`В2`ІІ х12; А1`В1` – натуральна величина).

П2

Дія

друга

–

щоб

поставити

пряму

проекціююче

положення,

треба

даному

В2

A2'

B2' В2'' ≡ A2''

випадку натуральну величину відрізка

А1`В1`

B''

розмістити перпендикулярно до осі х,

при

цьому відрізок переміщується у горизонтальній

A''

площині,

на

фронтальній

проекції

проекціюватиметься в точку (А2``≡ В2``).

В1

B1''

На

рис.

І.44. побудовано натуральну

B1'

A1'

величину

трикутника

методом

плоско-

н.в.

A1''

П1

паралельного переміщення. Горизонталь,

проведену

в трикутнику,

на

горизонтальній

б)

В2

проекції обертають перпендикулярно до осі ох

В2''≡ A2''

(перше

переміщення)

та

добудовують

A2'

B2'

фронтальну проекцію першого переміщення.

х12

На

фронтальній

проекції

трикутник

B1''

проекціюється в пряму А2`В2`С2`. Друга дія -

В1

B1'

фронтальну проекцію

трикутника обертаємо

до

положення,

паралельного

осі

ох

н.в

(А2``В2``С2``), та добудовуємо горизонтальну

A1'

проекцію другого переміщення. Отримана

проекція А1``В1``С1``

і буде натуральною

Рис.І.43

A1''

величиною трикутника.

B2`

C2``

A2``

B2``

A2`

П2

C2`

X П1

A1`

A1``

11`

B1`

B1``

h1`

Рис. I.44.

C1`

C1``

Приклад 2. Визначити		величину двогранного кута методом плоско-паралельного
	D2			D2'	B2''
				D2''
		B2	C2'	B2'
С2			C2'
С2
	A2			A2'	A2''
x П2				''	A2''
x П2				C2
П1	A1		А1'	B1'	A1''≡B1''
	B1			α
				D1''
С1	D1		'	D1'	''
С1		C1		C1

переміщення (рис.І.45)					Рис.І.45.
переміщення (рис.І.45)
Розв’язок. Якщо ребро двогранного кута спроекціювати в точку, площини, що його
утворюють, спроекціюються в лінії.			Саме кут між ц ими лініями і буде шуканим. Задача
зводиться до перетворення ребра АВ із прямої загального положення в проекціюючу пряму.
За прикладом на рис.І.43 двома діями переміщуємо відрізок АВ в проекціююче положення.
Слід зауважити, що разом з точками А і В необхідно переміщувати точки C I D. Після
виконання другої дії отриманий кут α між проекціями відрізків D1``-A1``≡ B1`` та С1``-A1``≡
B1`` і буде шуканим кутом при ребрі АВ.

III.Обертання навколо проекціюючих осей

Цей метод є практично аналогом методу плоскопаралельного переміщення, з одним доповненням: фігурам надають нове положення, обертаючи їх навколо чітко зафіксованих осей, перпендикулярних площинам проекцій. На рис. І.46 показано відрізок прямої загального положення АВ. Для визначення натуральної величини відрізка через його кінцеву точку В проведено горизонтально-проекціюючу вісь, навколо якої відрізок АВ повертають до фронтального положення. Точка В при цьому переміщується по дузі кола, площина якого перпендикулярна до вертикальної осі j. Натуральну величину показано на П2 подвійною прямою.

a)	П2				б)		j2
		j2					В2
		j2					н.в
	В2						н.в
	В2	н.в.	j			А2	А2'
						А2

	А2		А2'	x	П2
		B	А2'	x	П1		А1'
							А1'
							В1≡ j1
				A'
		А				А1
		А		А1'
			В1	А1'
		А1	В1
		А1		П1			Рис.І.46.
				П1

Визначення натуральної величини трикутника показано на рис.І.47 . Для цього в трикутнику проведено горизонталь h.

Перша дія – через точку А проводимо

горизонтально-проекціюючу	вісь	і,	та	на
горизонтальній проекції	обертаємо	навколо		неї

проекцію трикутника таким чином, щоб його горизонталь перетворилась в фронтальнопроекціюючу пряму. Далі добудовуємо фронтальну проекцію трикутника, який проекціюється в лінію

(А2`В2`С2`).

Друга дія – через точку С2` проводимо фронтально-проекціюючу вісь j , та на фронтальній

проекції обертаємо навколо неї проекцію А2`В2`С2`, до
горизонтального	положення	(А2``В2``С2``).

Добудовуємо горизонтальну проекцію, отриманий трикутник А2``В2``С2`` і буде натуральною величиною трикутника АВС.

		i2	B2`	B2
	A2≡ A2		h2		12
B ``	C2`≡ C2``≡ j2				C2
	A2``		A1≡ A1`≡ i1
X12	A2``		A1≡ A1`≡ i1	B1
	A2``			B1
				11	h1
B1``			1		C1
		11`			C1
		11`
	C1`≡ C1``		h1`	Рис. I.47.
	C1`≡ C1``	j1		Рис. I.47.

				III.	Обертання навколо ліній рівня
П2					Рис. І.48.					В2
П2		A			Рис. І.48.
		A
// до П1	А			h≡і							C2
// до П1	А										C2
		O
									A2		h2
х12									O2		12
	А1 А1			h1≡ і1				x П2
	н.в.ОА		O1					П1	B0
	н.в.ОА		O1						B0	B1
				G1					·	B1
				G1
					П1
					П1
					П11
На рис.І.49 показано площину загального											C1
положення,	задану		трикутним		відсіком.		Для		A1
визначення	натуральної			величини		відсіку			A1
визначення	натуральної			величини		відсіку			O1		h1
площини побудуємо в ній проекції горизонталі,											11
яка служитиме віссю обертання.											11
яка служитиме віссю обертання.
Точки А і 1, що належать осі обертання,
будуть нерухомими, а точки В та С будуть											С1I
обертатися навколо горизонталі , поки площина											С1I
не займе горизонтального положення. Точки О1
та О2 – проекції центру обертання для точки В.									В1I
В1О1 та В2О2 – проекції радіуса обертання.											Рис.І. 49.
Натуральна величина радіуса В0О1 знаходиться
методом прямокутного трикутника. Із точки О1 радіусом О1В0 проводимо коло до перетину з
лінією О1В1, при цьому вершина В займе своє нове положення. Такі ж побудови можна було
б використати і для вершини С. Але, якщо скористатися нерухомістю точки 1, то, провівши
лінію з точки В1		через точку 11			до перетину з перпендикуляром С1С11, отримаємо нове
положення точки		С. Натуральна величина трикутного відсіку виділена подвійними лініями.

БАГАТОГРАННИКИ.

Задання та зображення багатогранників.

Багатогранник (поліедр) – частина простору, обмежена площинами, що перетинаються.

Площини називають гранями, лінії перетину граней (сторони багатокутників) – ребрами,

точки перетину ребер – вершинами.

Утворення гранних поверхонь.

Поверхня – сукупність усіх послідовних положень будь якої прямої, що називається

твірною, яка переміщується в просторі за певним законом.

Призматична бічна поверхня утворюється рухом твірної q по ламаній напрямній d, яка

може бути плоскою і просторовою.

Послідовно рухаючись по точках 1, 2, 3,

5, твірна

Рис.І. 50.

а)

б)

займає положення q1,q2 ,q3,q4 ,q5 ,

при цьому

завжди

кут

нахилу

твірних

(ребер)

залишається

незмінним.

Тобто

ребра

призматичної бічної поверхні паралельні між

собою (рис.І.50а).

Пірамідальна

бічна

поверхня

утворюється послідовним рухом твірної q по

ламаній напрямній d. Твірна проходить через

зафіксовану

точку

яка

називається

вершиною (рис.І.50б).

Призматичну

поверхню представляють, як

а)

б)

частковий

випадок

пірамідальної,

у випадку,

коли S нескінченно віддалена.

В загальному випадку призматична та

П2

пірамідальна поверхні представлені на рис.І.51.

Якщо

вершина

обрана

невласною

точкою

П1

(рис.І.51а), одержимо призматичну поверхню з

паралельними між собою ребрами.

Якщо

вершина

вибрана

точці

отримаємо

Рис.І. 51.

пірамідальну поверхню.

Призма, піраміда, призматоїди.

Поліедри – найпростіші просторові форми, які використовуються з давніх часів в будівництві та техніці. З усіх поліедрів, крім правильних, практичне значення мають піраміди, призми та призматоїди.

Пірамідою називають багатогранник, у якого всі грані, крім однієї, мають спільну вершину, яка є вершиною піраміди, а бічні грані - трикутники (рис.І.52а).

Призма – це багатогранник, обмежений призматичною поверхнею та двома площинами, паралельними між собою. Ці площини є основами призми, грані призматичної поверхні називаються бічними гранями призми, а ребра призматичної поверхні – ребрами призми (рис.І.52б). Якщо ребра призми перпендикулярні до її основи, призму називають прямою, якщо ребра нахилені під довільним кутом – похилою.

Призматоїдом називають багато-гранник, всі бічні грані якого – трикутники або трапеції. Основи призматоїда найчастіше паралельні одна одній та є довільними багатокутниками. На рис.І.52в показано призматоїд, нижньою та верхньою основою якого є квадрати.

Пірамідальні та призматичні багато-гранники можуть бути прямими і похилими, в залежності від положення ребер відносно площини проекцій вони можуть займати загальне або окреме положення в просторі.

а) Піраміда	б) Призма	в) Призматоїд
	B2 A2	C2
	S2	E2	H2	G2
		E2	H2	G2

П2	B2	A2	C2	K2	L2	M2	A2≡B2	F1	C2≡D2
П1			C1	K1		M1	B1	F1	C1
			C1				B1		C1

	B1			C1			E1		G1
				B1			E1		G1
				B1	L1
					L1
		A1	S1	A1			A1	H1	D1
			S1				A1	H1	D1
									Рис. І.52.

Перетин багатогранників прямими та площинами.

Будь-яка січна площина перетинає задану площину по прямій лінії, а поверхню – по лінії її каркасу. При перетині багатогранників площиною утворюється плоский багатокутник, кожна вершина якого є точкою перетину ребрабагатогранника з площиною, а сторонабагатокутника є лінією перетину грані багатогранника з заданою площиною. Тобто знаходження лінії перетину зводиться до розв’язання кількох перших або других позиційних задач.

Перетин багатогранників площинами окремого положення

Перетин багатогранників з площинами рівня показано на рис.І.53а,б. При перетині піраміди і похилих призм лінія перетину будується за точками перетину ребер площиною. Для прямої призми одна проекція перерізу збігається зі слідом площини, а друга

– з проекцією її основи. При перетині призми горизонтальною площиною (рис.І.53а) одержимо чотирикутник 11213141, рівний основі. При перетині піраміди горизонтальною площиною одержимо багатокутник, подібний основі, в даному випадку це трикутник 112131.

а)						б)
	12	22	42	32	Σ2
						12	22	32	Γ2
			41					21
				31				21
	11			31
	11
		21				11		31
		21						31
в)	12	62				г)
	22								Т2
								42	Т2
								42
					52		32
					52
				32	42	12≡22		31
								31
	21	61			51	21
1	11			31	51	21
1	11				41			41
					41
						11
						11
Рис.І.53.

Перетин багатогранників площиною загального положення

У випадку, коли січна площина –

загального положення, а грані призми –

проекціюючі площини, побудова лінії перерізу

спрощується (рис.І.54). Необхідно знайти точки

перетину прямих m i n з горизонтально

проекціюючими гранями призми. В

разі

необхідності сліди граней можна продовжити

до перетину з прямими, що задають

січну

площину. Горизонтальна проекція косого

перерізу збігається з горизонтальною проекцією

призми.

На рис.І.55 показано побудову проекцій лінії

перетинупохилоїпіраміди з площиноюзагального

положення Т(m∩n). Задача вирішена

класичним

методом. Знайдені точки перетину кожного з ребер

піраміди з площиною (тричі розв’язана

перша

Рис.І.54.

позиційна задача).

Задачу такого типу можна також розв’язати

за допомогою методів перетворення креслень.

Перетворити площину загального положення в

проекціюючу(разоміз багатогранником).

На рис. І.

56 методом заміни площин проекцій

площину G (f02G h01G) загального положення

L2 42

переводять

на

площину

проекцій

П4

проекціююче

положення

G4.

Нова

площина

проекцій вводиться терпендикулярно до проекції

x П2

горизонтального сліду (h01G). Проекціюємо призму

П1

і січну площину на нову площину проекцій.

Для

цього на фронтальному сліді

f02G

вибирають

довільну точку 22 , знаходять її горизонтальну

проекцію

21,

та

будують

24.

Оскільки

горизонтальний слід

наП4 проекціюється в точку,

площина G – в пряму. На

П4 переноситься також

основа призми

ABC і ребра. За допомогою точки

1, довільно обраної на ребрі а, будуємо четверту

Σ1

проекцію цього ребра. Ребрас і b паралельні ребру

Рис.І.55.

Г1

а. Точки перетину ребер з січною площиною

наП1 таП2

визначаються за відповідністю.

визначені наП4

– K4,L4,M4.

Проекції лінії перетину

Перетин прямої з багатогранником

Для визначення точок перетину прямої з багатогранником використовують допоміжні проекціюючі площини. На рис. І.57 пряму АВ

заключають у фронтально-проекціюючу площину Г. В перерізі допоміжної січної площини з багатогранником отримаємо трикутник 123, в площині якого знаходиться пряма. Точки перетину К і М прямої з трикутником 123 будуть точками перетину прямої АВ з пірамідою. Видимою точкою перетину вважається та, яка належить видимій грані багатогранника. Видимість краще виявити методом конкуруючих точок.

			A2
	Г
		l2			B2
			K2		B2
		12	K2
				M2
		S		32		C2
x	П2	S
x	П2
	П1	S1		31
				31
						C1
		11		M1
		l1	1	21
				A1	B1
					B1	Рис.І.57.
						Рис.І.57.

		Взаємний перетин багатогранних поверхонь.
При взаємному перетині багатогранників можливі два випадки: врізання та наскрізне
проникнення.
а)				б)				Рис.І.59.
				б)
m2						22≡ 32		Г2
m2	12				12
	12	82				42≡52		Г21
		82	92			42≡52		Г21
n2			92
n2		32	71	102
		32
		42				92 ≡82		Г211
		42				92 ≡82		Г211
k2			61				62≡72	Г2111
	22		61	П2			62≡72	Г2111
			x	П2
		52	x	П1
A2			B2			91
A2		C2	B2
x12		C2				51
x12						51
A1			91			31	61
					11		61
				101			71
				101			71
11		81	B1≡61≡71			21
m1		51				41
	21	51				81
k1	21
k1	31
n1	31	41
		41
		C1
		C1
На рис.І.59а взаємно перетинаються дві призми: пряма і похила. З розгляду горизонтальної проекції призм
видно, що має місце наскрізне проникнення. Оскільки призма АВС пряма, то лінії взаємного перетину
лежатимуть на її горизонтально-проекціюючих гранях. Лишається за горизонтальними проекціями ліній
перетину побудувати їх фронтальні проекції. Трикутник входу 1-2-3 визначається за допомогою вертикальних
прямих відповідності. П’ятикутник виходу визначається трьома точками на ребрах похилої призми та двома
точками на вертикальному ребрі, що проходить через В. Для визначення точок на цьому ребрі грань СВ
продовжена до перетину з ребром m y точці 9, яка разом з точками 4 та 5 задасть на полі П2 трикутник. У
перетині цього трикутника з ребром, що проходить через точку В, знайдуться визначені точки.
При визначенні видимості береться до уваги те, що видимою буде лінія, яка утворилася в результаті
перетину двох видимих граней.
На рис. І.59б показано знаходження проекцій лінії перетину піраміди та призми. Ребра призми фронтально
проекціюючі. Точки 1, 10, 4≡5, 9≡8 – це точки перетину ребер піраміди з гранями призми. Точки2≡3, 6≡7 – точки
перетинуребер призмиз гранями піраміди. Це випадок врізання.

Перетин скатів даху.

Основні правила та методи побудови перетину гранних поверхонь мають практичне

застосування в будівництві при проектуванні скатного даху. Кут нахилу скатів даху

обирається в залежності від матеріалу та району будівництва. Лінії перетину скатів даху

називаються ребрами. Ребро, розміщене горизонтально, називають гребнем.

При однакових нахилах скатів даху та при організації їх навісів на одному

горизонтальному рівні (на умовній горизонтальній площині) перетин скатів

будується за

наступними положеннями:

а) горизонтальні проекції ліній перетину

Рис.І.62.

суміжних скатів проходять по бісектрисі кута

між їх слідами;

б) горизонтальні проекції ліній перетину

суміжних скатів проходять через точку

перетину горизонтальних слідів цих скатів;

в) якщо в будь-якій точці на

горизонтальній

проекції

покрівлі

перетинаються проекції двох ребер скатів, то

через цю точку проходить і проекція третього

ребра. В окремих випадках, коли в точці

перетинається

більша кількість

скатів,

через

цю точку може проходити більше ребер.

Розглянемо план будинку з двома

виступаючими частинами, одна з яких ширша,

друга

вища за основний об’єм

(рис.І.61). В

300

такому випадку краще розділити план на три

прямокутники

11213141, 51617181, 91101111121 і

12≡42

112≡102

перекрити окремо кожен з них. Проводимо

бісектриси кутів і знаходимо точки перетину

скатів

131,141,151,161, 191. Оскільки площини

101

1121141131 та 5161151 збігаються, ребра 51151 і

171

181

51151

будуть

існувати

на

відрізках

181151,

131

151

141

191

171151. Закінчуємо побудову проведенням

161

111

бісектрис внутрішніх кутів.

Щоб побудувати

121

фасад, звернемо увагу на те, що скати 1113141,

2131141 і

101111191 – фронтально проекціюючі

площини,

що

дозволяє

фронтальних

Рис.І.61.

проекцій точок

12≡42, 32≡22, 112≡102 провести

прямі під кутом 300 , а через проекції точок

131, 141, 151, 191 – лінії зв’язку.

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.05.2015898.13 Кб280Лабораторный практикум по АИС (12 лаб работ).docx
#
11.05.2015353.78 Кб12ЛГТУ методичка- менеджмент.pdf
#
17.03.201680.38 Кб16ЛГТУ. Бухучёт. 2015. Oformlenie.doc
#
11.05.2015346.18 Кб153ЛГТУ_sto-13-2011.pdf
#
17.12.20181.91 Mб7Лекц Микроэк-ка 1 семестр.doc2.doc
#
11.05.20152.18 Mб43Лекц.pdf
#
11.05.2015501.76 Кб27Лекції УІД.doc
#
11.05.20155.84 Mб767лекции для сам.работы.doc
#
11.05.2015102.4 Кб14Лекции для ТЛП по Метрологии.doc
#
11.05.2015333.82 Кб185Лекции по ЗПП.doc
#
14.09.2019261.63 Кб1лекции по ИТ_3базы_данных.doc