Б в Рис. 19. Таблица истинности и карта Карно

	00	01	11	10
0	000 1	001 1	011 0	010 0
1	100 0	101 1	111 0	110 1

а

Минимизация конъюнктивных нормальных форм

Минимизация КНФ производится аналогично рассмотренным методам минимизации ДНФ булевых функций, поэтому остановимся лишь на основных положениях.

Напомним, что конституентой нуля называется функция, принимающая значение 0 на одном наборе. Она выражается дизъюнкцией всех переменных функций. Например, набору 0110 соответствует конституента нуля x₁+x₂+x₃+x₄.

Имплицентойg булевой функции f называется функция, принимающая значение 0 на подмножестве нулевых наборов функции f.

Простой имплицентойфункции f называется элементарная дизъюнкция, являющаяся имплицентой функции f, причем никакая ее собственная часть имплицентой функции f не является.

Задачей минимизации КНФ является определение минимальной КНФ. Эта задача также решается в два этапа: поиск сокращенной КНФ (конъюнкция всех простых имплицент) и затем нахождение минимальной КНФ. Второй этап минимизации выполняется с помощью таблицы Квайна точно так же, как и при поиске минимальной ДНФ, так как возможны только два варианта: либо данная простая имплицента поглощает данную конституенту нуля, либо нет в соответствии с соотношением поглощения:

(A v x)A = A.

Что касается первого этапа - поиска всех простых имплицент, то практически все методы минимизации ДНФ имеют свои аналоги для КНФ. Рассмотрим это подробнее.

Соотношение склеивания по Квайну:

Соотношение склеивания по Блейку:

Метод Нельсона в применении к задаче минимизации КНФ: раскрытие скобок в произвольной ДНФ функции и выполнение поглощений приводит к сокращенной КНФ. Предполагаются скобки в начале и конце каждого элементарного произведения исходной ДНФx₁x₂+x₁x₂и использование второго дистрибутивного закона. Например, функция, заданная минимальной ДНФ дает возможность определить ее сокращенную КНФ:

По диаграмме Вейча поиск минимальной КНФ осуществляется так же просто, как и в случае ДНФ. Отличие состоит лишь в том, что анализируются нулевые наборы и переменные выписываются с инверсиями. Например, для функции, заданной диаграммой (рис. 20), минимальной КНФ является

Д

Рис. 20. Карта Вейча для поиска f_MКНФ

ля сравнения найдем минимальную ДНФ:

В данном случае ДНФ оказалась проще. В общем случае о сравнительной сложности минимальных ДНФ и КНФ нельзя говорить заранее.

Минимизация не полностью определенных фал

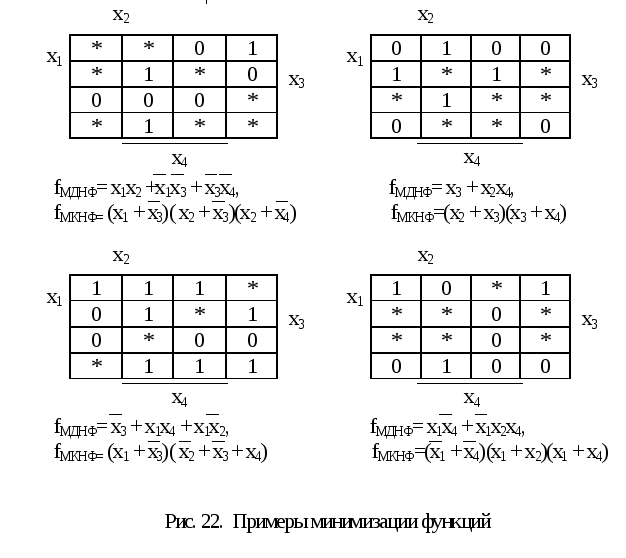
Если при синтезе логической схемы, реализующей некоторую ФАЛ n переменных, окажется, что некоторые наборы из общего числа 2ⁿ никогда не смогут появиться на входах схемы, то данная логическая функция не определена на этих наборах. Тогда 2ⁿнаборов переменных можно подразделить на три группы: множество наборов L, на которых функция принимает единичное значение, множество наборов D, на которых функция принимает нулевое значение, и множество наборов N, на которых функция не определена (неопределенные наборы). ФАЛ, содержащая неопределенные наборы, называется не полностью или частично определенной. Неопределенные наборы могут быть использованы для улучшения качества минимизации. При этом неопределенные наборы (при минимизации, например, картами Вейча, Карно) могут участвовать в образовании контуров как с единичными, так и с нулевыми наборами. Это приводит к формированию более простой минимизированной логической функции.

	x2
x1	1		1	*
	1	*
	x3

З

Рис.21. Карта Вейча

вездочками на карте (рис. 21) отмечены наборы, на которых функцияfне определена. Если не учитывать неопределенные наборы, то минимальная форма будет иметь вид: .В случае если неопределенные наборы участвуют в образовании контуров, а следовательно, иf_МДНФ, то функция примет следующий вид: . Таким образом, схемная реализация получен- нойf_МДНФбудет ”дешевле”.

Приведем примеры минимизации частичных булевых функций (рис.22).