Матричные методы умножения

Кроме рассмотренных методов ускоренного умножения существуют методы умножения, основанные на использовании матриц промежуточных результатов.

Пусть имеем сомножители:

Мн = А = а_n ... a₂ a₁

М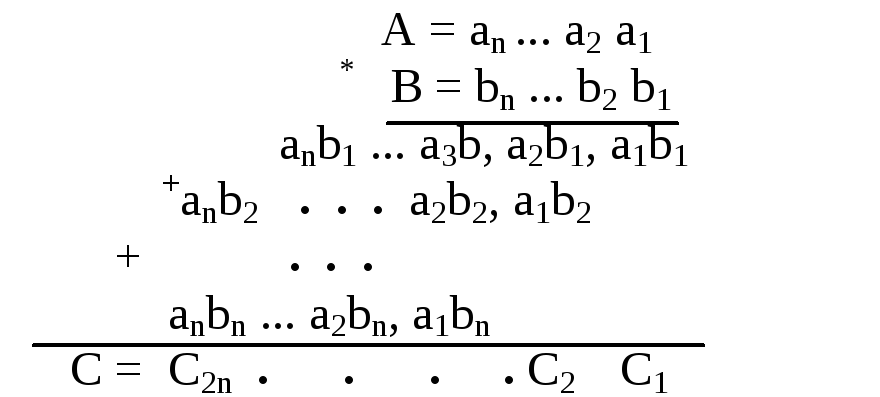т = B = b_n ... b₂ b₁

Рассмотрим схему умножения чисел согласно алгоритму Б. Данная схема умножения может быть представлена в виде матрицы (табл.3).

Каждый элементa_i b_j ( i, j = 1, n)принимает значение 0 или 1. Произведение A∙B может быть получено, если суммировать элементы матрицы (по диагонали).

⁺

Для суммирования по столбцам могут быть использованы счетчики. Однако при достаточно большом значении величины nпотребуются счетчики с большим числом входов, что существенно увеличит время сложения. Но этот принцип умножения может быть реализован на устройствах, имеющих не более трех входов. В качестве их могут быть использованы одноразрядные двоичные сумматоры и полусумматоры.

На рис. 10 приведена структурная схема устройства умножения для реализации матричного алгоритма.

Реализация методов матричного умножения требует большего количества оборудования, чем метод последовательного умножения, и дает больший выигрыш во времени. В связи с увеличением степени интеграции элементной базы ограничения по количеству оборудования становятся не столь строгими.

Машинные методы деления

Деление - простое многократное вычитание делителя вначале из делимого, затем из остатков. Введем обозначения, используемые ниже: Дм - делимое, Дт - делитель, А_i– очередной (i-й) остаток, Чт – частное. Известны два основных подхода к операции деления:

• с восстановлением остатков;

• без восстановления остатков.

Независимо от метода деления после каждого вычитания делителя формируется цифра частного. Операция деления является операцией, дающей не всегда точный результат. Поэтому признаком окончания операции деления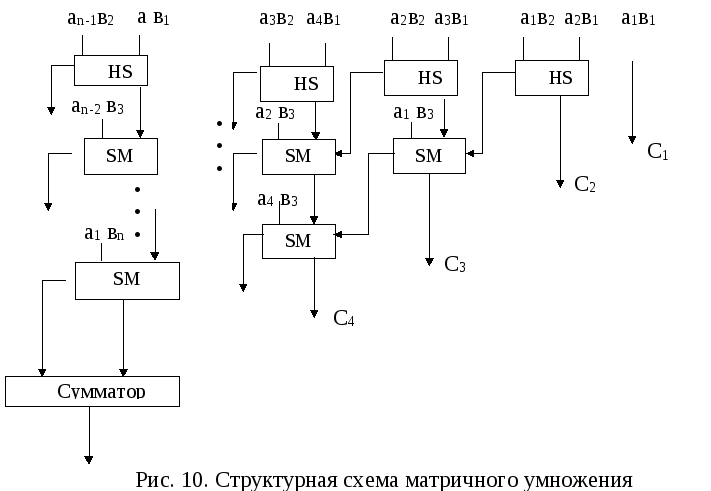

может быть достижение заданной точности (по числу сдвиговых сигналов). Если при выполнении деления получен нулевой i-й остаток, то деление прекращается и в оставшиеся разряды частного записываются нули. Первым шагом деления двух чисел машиной является пробное вычитание, выявляющее соотношение между делимым и делителем. При делении в случае переполнения следует: для чисел с фиксированной запятой процесс остановить, с плавающей запятой продолжить до конца, а потом, после получения последней n-й цифры частного, число сдвигается вправо на один разряд с добавлением единицы к порядку, равному разности порядков делимого и делителя.

Деление чисел в прямых кодах

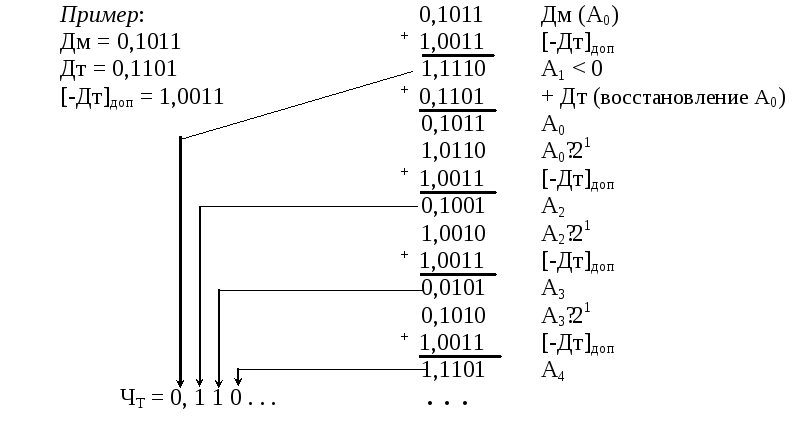
Алгоритмделения с восстановлением остаткасостоит в следующем.

1. Выполняется пробное вычитание с формированием первого остатка A₁=[Дм]_доп+[-Дт]_доп. Далее, если А₁< 0, то в первый разряд, расположенный слева от запятой, заносится ноль (0), иначе единица (1) – переполнение и переход к пункту 5.

2. Если А_i< 0, то восстанавливаем предыдущий остаток A_i=A_i+[Дт]_доп.

3. Формирование очередного остатка. A_i+1=A_i∙2+[-Дт]_доп если A_i+1<0, то в очередной разряд частного справа от запятой записывается ноль (Чт(n)=0), иначе записывается единица (Чт(n)=1).

4. Если достигнута заданная точность частного или получен нулевой остаток A_i+1, то процесс деления окончен и осуществляется переход к пункту 5, иначе переходим к пункту 2 алгоритма.

5. Окончание алгоритма.

Из рассмотренного алгоритма видно следующее:

1) необходимо затрачивать время на восстановление остатка;

2) процесс деления нерегулярный, в зависимости от делимого и делителя

частное будет содержать нулей больше или меньше, и чем больше нулей, тем больше требуется времени на восстановление остатков.

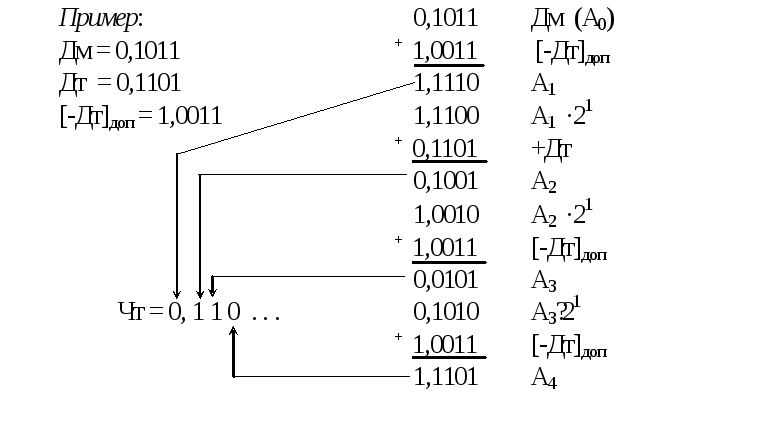
Рассмотрим пример деления чисел.

Как видно из примера, для получения остатка А_i+2необходимо выполнить

А_i+2= ( A_i+1 + Д_T) ∙ 2¹- Д_T= A_i+1∙ 2¹+ 2Д_T- Д_T= A_i+1∙ 2¹+ Д_T

Из этого следует, что восстанавливать остаток необязательно. Достаточно сдвинуть полученный отрицательный остаток влево на один разряд и добавить делитель. Это является основой алгоритма для выполнения деления без восстановления остатка.

Алгоритмделения без восстановленияостатка.

1. Выполняется пробное вычитание с формированием первого остатка A₁=[Дм]_доп+[-Дт]_доп. Далее, если А₁< 0, то в первый разряд, расположенный слева от запятой, заносится ноль (0), иначе единица (1) – что является признаком переполнение и ос4уществляется переход к пункту 5.

2. Формирование очередного остатка. Если А_i< 0, то A_i+1=A_i∙2+[Дт]_доп, иначеA_i+1=A_i∙2+[-Дт]_доп.

3. Если А_i+1< 0, то в очередной разряд частного справа от запятой записывается ноль (Чт(n)=0), иначе записывается единица (Чт(n)=1).

4. Если достигнута заданная точность частого или получен нулевой остаток A_i+1, то процесс деления окончен и осуществляется переход к пункту 5, иначе переходим к пункту 2 алгоритма.

5. Окончание алгоритма.