
- •1.Понятие числовых множеств. Действия над числовыми множествами.
- •2.Числовые промежутки. Окрестность точки.
- •3.Функция.График функции. Способы задания функции.
- •4.Основные характеристики функции: монотонность, четность, периодичность.
- •5.Обратная функция.
- •6.Сложная функция.
- •7.Основные элементарные функции; (степенная, тригонометрические, обратно-тригонометрические, показательная, логарифмическая) их свойства и графики.
- •Корень n-ой степени.
- •Корень n-ой степени, n - четное число.
- •Корень n-ой степени, n - нечетное число.
- •Степенная функция с нечетным положительным показателем.
- •Степенная функция с четным положительным показателем.
- •Степенная функция с нечетным отрицательным показателем.
- •Степенная функция с четным отрицательным показателем.
- •Степенная функция с рациональным или иррациональным показателем, значение которого больше нуля и меньше единицы.
- •Степенная функция с нецелым рациональным или иррациональным показателем, большим единицы.
- •Степенная функция с действительным показателем, который больше минус единицы и меньше нуля.
- •Степенная функция с нецелым действительным показателем, который меньше минус единицы.
- •Показательная функция.
- •Логарифмическая функция.
- •Тригонометрические функции, их свойства и графики.
- •Обратные тригонометрические функции, их свойства и графики.
- •8.Числовые последовательности.
- •Определение
- •Примеры
- •Операции над последовательностями
- •9.Предел числовой последовательности.
- •10.Предельный переход в неравенствах.
- •11.Предел функции в точке.
- •Левый и правый пределы функции
- •13.Предел функции при х→0
- •14.Бесконечно большая функция. Ответ - Бесконечно большая функция
- •15.Определение и основные свойства бесконечно малых функции.
- •16.Связь между функцией, пределом и бесконечно малой величиной.
- •17.Основные теоремы о пределах.
- •Предел монотонной функции
- •19.Первый замечательный предел.
- •Следствия из первого замечательного предела
- •20.Второй замечательный предел(б/д).
- •Следствия из второго замечательного предела
- •21.Сравнение бесконечно малых.
- •22. Основные теоремы о б.М.
- •23.Непрерывность функции в точке и на промежутке.
- •24.Точки разрыва функции и их классификация.
- •25.Основные теоремы о непрерывных функциях.
- •26.Свойства функций, непрерывных на отрезке (б/д). Ответ - Свойства функций непрерывных на отрезке:
- •27.Производная; Ее геометрический и физический смысл.
- •28.Связь между непрерывность. И дифференцируемостью функции.
- •31.Производная обратной функции.
- •32.Производные основных элементарных функций; таблица производных (вывод).
- •33.Дифференцирование неявных функций.
- •34. Дифференцирование параметрический заданных функций.
- •35.Логарифмическое дифференцирование.
- •38.Основные теоремы о дифференциалах.
- •39.Применение дифференциала к приближенным вычислениям.
- •40.Дифференциалы высших порядков. Инвариантность формы dy.
- •41.Теорема Ролля
- •54.Неопределенный интеграл: определение, геометрический смысл.
- •56. Основные свойства интеграла.
- •57. Таблица основных интегралов.
- •58.Интегрирование заменой переменной.
- •59.Интегрирование по частям
- •61.Основыне сведения о разложении многочленов
- •62.Теоремы о разложении рациональной дроби на сумму элементарных дробей
- •63.Основная тригонометрическая подстановка.
Обратные тригонометрические функции, их свойства и графики.
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки "арк" обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:
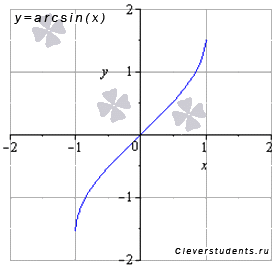
Свойства функции арксинус y = arcsin(x).
Областью определения функции арксинус является интервал от минус единицы до единицы включительно:
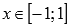 .
.Область значений функции y = arcsin(x):
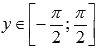 .
.Функция арксинус - нечетная, так как
 .
.Функция y = arcsin(x) возрастает на всей области определения, то есть, при
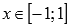 .
.Функция вогнутая при
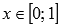 ,
выпуклая при
,
выпуклая при .
.Точка перегиба (0; 0), она же ноль функции.
Асимптот нет.
К началу страницы
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:
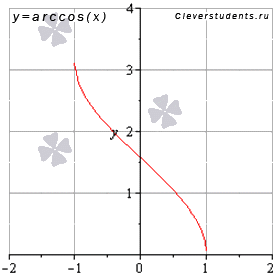
Свойства функции арккосинус y = arccos(x).
Область определения функции арккосинус:
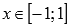 .
.Область значений функции y = arccos(x):
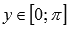 .
.Функция не является ни четной ни нечетной, то есть, она общего вида.
Функция арккосинус убывает на всей области определения, то есть, при
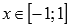 .
.Функция вогнутая при
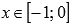 ,
выпуклая при
,
выпуклая при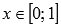 .
.Точка перегиба
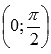 .
.Асимптот нет.
К началу страницы
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:

Свойства функции арктангенс y = arctg(x).
Область определения функции y = arctg(x):
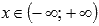 .
.Область значений функции арктангенс:
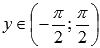 .
.Функция арктангенс - нечетная, так как
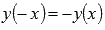 .
.Функция возрастает на всей области определения, то есть, при
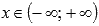 .
.Функция арктангенс вогнутая при
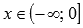 ,
выпуклая при
,
выпуклая при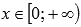 .
.Точка перегиба (0; 0), она же ноль функции.
Горизонтальными асимптотами являются прямые
 при
при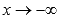 и
и при
при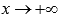 .
На чертеже они показаны зеленым цветом.
.
На чертеже они показаны зеленым цветом.
К началу страницы
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:
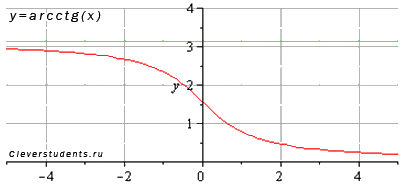
Свойства функции арккотангенс y = arcctg(x).
Областью определения функции арккотангенс является все множество действительных чисел:
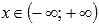 .
.Область значений функции y = arcctg(x):
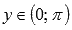 .
.Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
Функция убывает на всей области определения, то есть, при
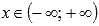 .
.Функция вогнутая при
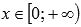 ,
выпуклая при
,
выпуклая при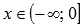 .
.Точка перегиба
 .
.Горизонтальными асимптотами являются прямые
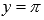 при
при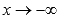 (на
чертеже показана зеленым цветом)
и y = 0 при
(на
чертеже показана зеленым цветом)
и y = 0 при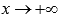 .
.
8.Числовые последовательности.
Ответ - Числовая последовательность — это последовательностьэлементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.
Определение
Пусть ![]() —
это либо множество вещественных чисел
—
это либо множество вещественных чисел![]() ,
либо множество комплексных чисел
,
либо множество комплексных чисел![]() .
Тогда последовательность
.
Тогда последовательность![]() элементов
множества
элементов
множества![]() называется числовой
последовательностью.
называется числовой
последовательностью.
Примеры
Функция
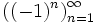 является
бесконечной последовательностьюцелых
чисел. Начальные отрезки этой
последовательности имеют вид
является
бесконечной последовательностьюцелых
чисел. Начальные отрезки этой
последовательности имеют вид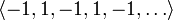 .
.Функция
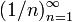 является
бесконечной последовательностьюрациональных
чисел. Начальные отрезки этой
последовательности имеют вид
является
бесконечной последовательностьюрациональных
чисел. Начальные отрезки этой
последовательности имеют вид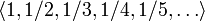 .
.Функция, сопоставляющая каждому натуральному числу
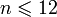 одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида
одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида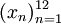 .
В частности, пятым членом
.
В частности, пятым членом этой
последовательности является слово
«май».
этой
последовательности является слово
«май».
