57. Таблица основных интегралов.

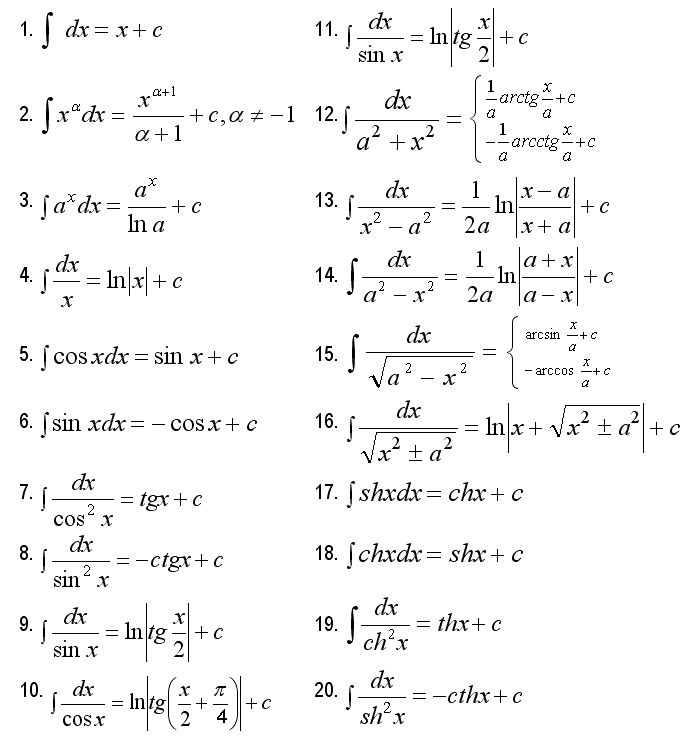
58.Интегрирование заменой переменной.

Ответ - Одним из наиболее мощных методов интегрирования является замена переменной в интеграле. Поясним суть этого метода. Пусть , тогда

Но в силу инвариантности формы дифференциала равенство остается справедливым и в случае, когда— промежуточный аргумент, т.е.. Это значит, что формулаверна и при. Таким образом,

, или .

Итак, если является первообразной дляна промежутке, а— дифференцируемая на промежуткефункция, значения которой принадлежат, то— первообразная для, и, следовательно,

Эта формула позволяет свести вычисление интеграла к вычислению интеграла. При этом мы подставляем вместопеременную, а вместодифференциал этой переменной, т. е.. Поэтому полученная формула называется формулой замены переменной под знаком неопределенного интеграла. Она используется на практике как "слева направо", так и "справа налево". Метод замены переменной позволяет сводить многие интегралы к табличным. После вычисления интеграланадо снова заменитьна.

59.Интегрирование по частям

Ответ - Рассмотрим функции и, которые имеют непрерывныепроизводные. Согласно свойствам дифференциалов, имеет место следующее равенство:

Проинтегрировав левую и правую части последнего равенства, получим:

Полученное равенство перепишем в виде:

Эта формула называется формулой интегрирования по частям. С ее помощью интеграл можно свести к нахождению интеграла, который может быть более простым.

Замечание

В некоторых случаях формулу интегрирования частями нужно применять неоднократно.

Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:

1) ;;

Здесь - многочлен степени,- некоторая константа. В данном случае в качестве функцииберется многочлен, а в качестве- оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяетсяраз.

61.Основыне сведения о разложении многочленов

Ответ – Любой многочлен степени n вида представляется произведением постоянного множителя при старшей степении n линейных множителей, i=1, 2, …, n, то есть, причем, i=1, 2, …, nявляются корнями многочлена.

Эта теорема сформулирована для комплексных корней , i=1, 2, …, n и комплексных коэффициентов, k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители.

Если коэффициенты , k=0, 1, 2, …, n – действительные числа, то комплексные корни многочлена ОБЯЗАТЕЛЬНО будут встречаться комплексно сопряженными парами.

К примеру, если корни имногочленаявляются комплексно сопряженными, а остальные корни действительные, то многочлен представится в виде, где

Замечание.

Среди корней многочлена могут быть повторяющиеся.

Доказательство теоремы проводится с использованием основной теоремы алгебры иследствия из теоремы Безу.

Основная теорема алгебры.

Всякий многочлен степени n имеет по крайней мере один корень (комплексный или действительный).

Теорема Безу.

При делении многочлена на (x-s) получается остаток, равный значению многочлена в точке s, то есть, гдеесть многочлен степени n-1.

Следствие из теоремы Безу.

Если s – корень многочлена , то.

Это следствие будем достаточно часто употреблять при описании решения примеров.