26.Свойства функций, непрерывных на отрезке (б/д). Ответ - Свойства функций непрерывных на отрезке:

1. Теорема Вейерштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения.

2. Непрерывная на отрезке  функция является ограниченной на этом отрезке.

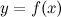3. Теорема Больцано-Коши. Если функция  является непрерывной на отрезке  и принимает на концах этого отрезка неравные между собой значения, то есть , , 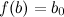то на этом отрезке функция принимает и все промежуточные значения между  и  .

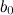4. Если функция 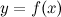, которая непрерывна на некотором отрезке , принимает на концах отрезка значения разных знаков, то существует такая точка 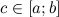 такая, что  .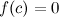

27.Производная; Ее геометрический и физический смысл.

Ответ -

28.Связь между непрерывность. И дифференцируемостью функции.

Ответ -

29.вывод формул:(u+v)’ ; (uv)’ ; (u/v)’.

Ответ -

30.Производная сложной функции.

Производная сложной функции.

Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать какf(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а - целая рациональная функция (смотритеклассификацию элементарных функций), тогда.

В свою очередь, g(x) также может быть сложной функцией. Например, . Условно такое выражение можно обозначить как. Здесь f – функция синуса,- функция извлечения квадратного корня,- дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом.

Часто можно слышать, что сложную функцию называют композицией функций.

Формула нахождения производной сложной функции.

31.Производная обратной функции.

Ответ

Производная обратной функции.

Прим. Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, - это производная функции f(x) по x.

правило нахождения производной обратной функции.

Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах исоответственно. Если в точкесуществует конечная отличная от нуля производная функции f(x), то в точкесуществует конечная производная обратной функции g(y), причем. В другой записи.

Можно это правило переформулировать для любого x из промежутка , тогда получим.

Пример:

Найдем обратную функцию для натурального логарифма (здесь y – функция, аx - аргумент). Разрешив это уравнение относительно x, получим(здесь x – функция, а y – ее аргумент). То есть,ивзаимно обратные функции.

32.Производные основных элементарных функций; таблица производных (вывод).

Ответ -

Таблица производных. Вывод формул.

Производная постоянной.

При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции. Запишем предел отношения приращения функции к приращению аргумента при:

Таким образом, производная постоянной функции равна нулю на всей области определения.

Производная степенной функции.

Формула производной степенной функции имеет вид , где показатель степени p– любое действительное число.

Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …

Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:

Для упрощения выражения в числителе обратимся к формуле бинома Ньютона:

Следовательно,

Этим доказана формула производной степенной функции для натурального показателя.

При доказательстве формулы для любого действительного p, отличного от нуля, воспользуемся логарифмической производной (не путайте с производной логарифмической функции). Для понимания процесса, рекомендуем сначала ознакомиться с производной логарифмической функции, а также разобраться с разделами теории производная неявно заданной функции и производная сложной функции.

Следует рассмотреть два случая: при положительных x и отрицательных x.

Сначала будем полагать . В этом случае. Выполним логарифмирование равенствапо основанию e и применим свойство логарифма: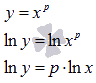

Пришли к неявно заданной функции. Находим ее производную:

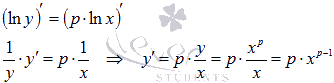
Осталось провести доказательство для отрицательных x.

Когда показатель p представляет собой четное число, то степенная функция определена и при, причем является четной (смотрите разделосновные элементарные функции, их свойства и графики). То есть, . В этом случаеи также можно использовать доказательство через логарифмическую производную.

Когда показатель p представляет собой нечетное число, то степенная функция определена и при , причем является нечетной. То есть,. В этом случаеи логарифмическую производную использовать нельзя. Для доказательства формулыв этом случае можно воспользоватьсяправилами дифференцирования и правилом нахождения производной сложной функции:

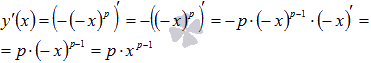
Последний переход возможен в силу того, что если p - нечетное число, то p-1 либо четное число, либо нуль (при p=1), поэтому, для отрицательных x справедливо равенство .

Таким образом, формула производной степенной функции доказана для любого действительного p.

Производная показательной функции.

Вывод формулы производной приведем на основе определения:

Пришли к неопределенности. Для ее раскрытия введем новую переменную , причемпри. Тогда. В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел:

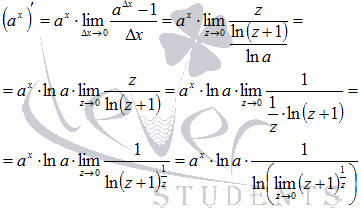
Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:

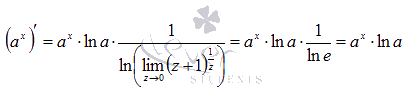
Производная логарифмической функции.

Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:

Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.

Производные тригонометрических функций.

Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.

По определению производной для функции синуса имеем .

Воспользуемся формулой разности синусов:

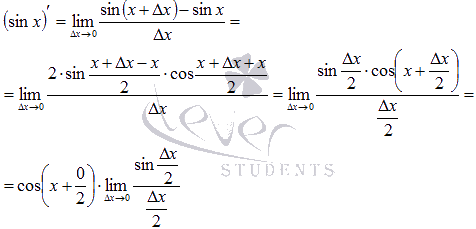
Осталось обратиться к первому замечательному пределу:

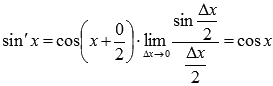
Таким образом, производная функции sin x есть cos x.

Абсолютно аналогично доказывается формула производной косинуса.

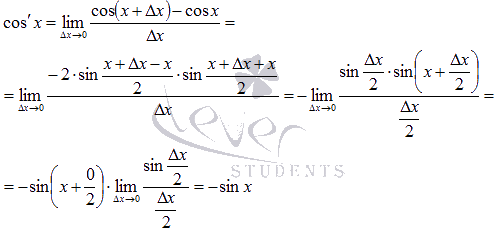
Следовательно, производная функции cos x есть –sin x.

Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (производная дроби).